
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгоритм восходящего разбора с возвратами
|
|
|
|
Мы опишем восходящий разбор в виде алгоритма синтаксического анализа, который называют алгоритмом типа «перенос-свертка». Он представляет собой по существу правый анализатор, который перебирает всевозможные обращенные правые выводы, совместимые с входной цепочкой. Один шаг алгоритма состоит в считывании цепочки, расположенной в верхней части магазина, чтобы выяснить, образуют ли верхние символы правую часть какого-нибудь правила. Если да, то производится свертка, заменяющая эти символы левой частью того самого правила. Если возможна более чем одна свертка, го эти свертки упорядочиваются произвольным образом и применяется первая из них.
Если свертка невозможна, то в магазин переносится следующий входной символ и процесс продолжается, как прежде. Всегда перед переносом делается попытка свертки. Если мы дошли до конца цепочки, а свертка все еще невозможна, то надо вернуться к последнему шагу, на котором была сделана свертка. Если здесь возможна другая свертка, надо испытать ее.
Этот метод можно рассматривать как процедуру прослеживания всевозможных последовательностей тактов недетерминированного правого анализатора для данной грамматики. Однако так же, как в случае нисходящего разбора, надо избегать ситуаций, в которых число возможных последовательностей тактов бесконечно.
Одна такая ловушка оказывается тогда, когда грамматика содержит циклы, т. е. выводы вида  для некоторого нетерминала
для некоторого нетерминала 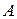 . Число частичных деревьев может быть в этом случае бесконечным, так что грамматики с циклами мы исключим из рассмотрения. Трудности создаются также
. Число частичных деревьев может быть в этом случае бесконечным, так что грамматики с циклами мы исключим из рассмотрения. Трудности создаются также 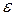 -правилами, так как тогда можно проделать произвольное число сверток, при которых пустая цепочка «свертывается» к нетерминалу. Восходящий разбор можно расширить так, чтобы он охватывал грамматики с
-правилами, так как тогда можно проделать произвольное число сверток, при которых пустая цепочка «свертывается» к нетерминалу. Восходящий разбор можно расширить так, чтобы он охватывал грамматики с 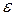 -правилами, но пока для простоты мы предпочитаем обходиться без
-правилами, но пока для простоты мы предпочитаем обходиться без 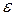 -правил.
-правил.
Для реализации алгоритма также будем использовать два магазина 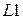 и
и 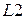 .
.
Вход: КС-грамматика 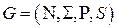 без циклов и пустых правил (ВСЕХ!!!) и входная цепочка
без циклов и пустых правил (ВСЕХ!!!) и входная цепочка  . Предполагается, что правила из
. Предполагается, что правила из 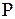 занумерованы числами
занумерованы числами 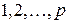 .
.
Выход: Один обращенный правый разбор, если таковой существует. В противном случае – слово «ошибка».
Метод:
1. Произвольным образом упорядочить правила;
2. Определим конфигурацию алгоритма как упорядоченную четверку вида  , где
, где 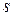 - состояние алгоритма,
- состояние алгоритма, 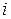 - номер позиции указателя чтения входной цепочки (предполагается, что
- номер позиции указателя чтения входной цепочки (предполагается, что 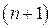 -м входным символом является специальный символ (маркер)
-м входным символом является специальный символ (маркер) 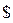 , означающий конец входной строки),
, означающий конец входной строки), 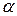 - содержимое первого магазина
- содержимое первого магазина 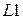 (верх которого расположен справа),
(верх которого расположен справа),  - содержимое второго магазина
- содержимое второго магазина 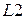 (верх которого расположен слева).
(верх которого расположен слева).
Алгоритм может находиться в одном из трех состояний 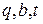 , где
, где 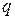 - состояние нормальной деятельности,
- состояние нормальной деятельности,  - состояние возврата,
- состояние возврата, 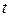 - заключительное состояние.
- заключительное состояние.
В магазине 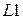 будет храниться цепочка терминалов и нетерминалов, из которой выводится часть входной цепочки, расположенная слева от входного указателя. В магазине
будет храниться цепочка терминалов и нетерминалов, из которой выводится часть входной цепочки, расположенная слева от входного указателя. В магазине 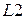 будет храниться история переносов и сверток, необходимых для получения из входной цепочки содержимого магазина
будет храниться история переносов и сверток, необходимых для получения из входной цепочки содержимого магазина 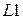 ;
;
3. Начальная конфигурация алгоритма - 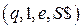 ;
;
4. Сам алгоритм работает так. Начинаем с попытки применить шаг 1.
Шаг 1. Попытка свертки
 ,
,
где правило 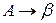 принадлежит
принадлежит 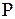 и имеет номер
и имеет номер 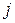 ,
,  - первая альтернатива для нетерминала
- первая альтернатива для нетерминала 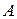 и является суффиксом цепочки
и является суффиксом цепочки  . Номер этого правила записывается в
. Номер этого правила записывается в 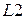 . Пока применим продолжаем Шаг 1, иначе, переход к шагу 2;
. Пока применим продолжаем Шаг 1, иначе, переход к шагу 2;
Шаг 2. Перенос
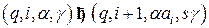 ,
,
если  . Затем перейти к шагу 1.
. Затем перейти к шагу 1.
Если  перейти к шагу 3.
перейти к шагу 3.
Здесь при выполнении этого шага 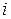 -й входной символ переносится в верхнюю часть магазина
-й входной символ переносится в верхнюю часть магазина 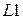 , позиция входного указателя увеличивается и в магазин
, позиция входного указателя увеличивается и в магазин 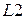 записывается
записывается 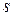 , чтобы указать, что сделан перенос;
, чтобы указать, что сделан перенос;
Шаг 3. Допускание
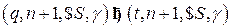
Достигнут конец входной цепочки и найдена правовыводимая цепочка, совпадающая с входной. Обращенный правый разбор 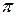 входной цепочки
входной цепочки 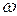 восстанавливается по цепочке
восстанавливается по цепочке 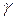 с помощью гомоморфизма
с помощью гомоморфизма  , где
, где  . После этого остановиться.
. После этого остановиться.
Если шаг 3 неприменим, то перейти к шагу 4;
Шаг 4. Переход в состояние возврата

при условии, что 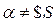 . Переход к шагу 5;
. Переход к шагу 5;
Шаг 5. Возврат.
a.
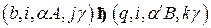 ,
,
если 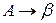 правило из
правило из 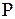 с номером
с номером 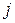 , а следующим правилом в упорядочении, правая часть которого (правила) является суффиксом цепочки
, а следующим правилом в упорядочении, правая часть которого (правила) является суффиксом цепочки  , является правило
, является правило  с номером
с номером 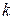 . (Заметим, что
. (Заметим, что 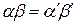 ). Затем перейти к шагу 1.
). Затем перейти к шагу 1.
Примечание. Здесь происходит возврат к предыдущей свертке и делается попытка свертки с помощью следующей альтернативы;
b.
 ,
,
если 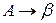 правило из
правило из 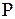 с номером
с номером 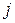 и для цепочки
и для цепочки  не остается никакой другой свертки. Перейти к шагу 5.
не остается никакой другой свертки. Перейти к шагу 5.
Примечание. Если других сверток не существует, надо «взять назад» данную свертку и продолжать возврат, оставляя входной указатель на позиции  ;
;
c.
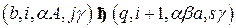 ,
,
если 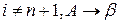 правило из
правило из 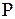 с номером
с номером 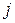 и для цепочки
и для цепочки  не остается никакой другой свертки. Здесь символ
не остается никакой другой свертки. Здесь символ 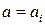 переносится в магазин
переносится в магазин 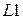 , а символ
, а символ 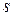 поступает в
поступает в 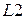 . Перейти к шагу 1.
. Перейти к шагу 1.
Примечание. Мы вернулись к предыдущей свертке и, так как других сверток нет попробуем сделать перенос;
d.
 ,
,
если наверху магазина 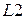 находится символ переноса
находится символ переноса 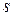 .
.
Примечание. Здесь в позиции 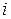 исчерпаны все альтернативы и надо «взять назад» операцию переноса. Входной указатель сдвигается влево, терминальный символ устраняется из
исчерпаны все альтернативы и надо «взять назад» операцию переноса. Входной указатель сдвигается влево, терминальный символ устраняется из 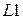 , а символ переноса
, а символ переноса 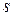 - из
- из 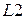 .
.
Если этот шаг не выполним, объявить об ошибке.
Пример №1
Задание.
Пусть задана КС-грамматика 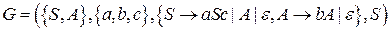 . Требуется построить обращенный правый разбор для цепочек вида
. Требуется построить обращенный правый разбор для цепочек вида

|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2022; Нарушение авторских прав?; Мы поможем в написании вашей работы!