Практически любую задачу можно свести к задаче, решаемой нейросетью

В табл.2 показано, каким образом следует сформулировать в терминах нейросети задачу распознавания рукописных букв.

Поясним, зачем требуется выбирать выход с максимальным уровнем сигнала. Дело в том, что уровень выходного сигнала, как правило, может принимать любые значения из какого-то отрезка. Однако, в данной задаче нас интересует не аналоговый ответ, а всего лишь номер категории (номер буквы в алфавите). Поэтому используется следующий подход - каждой категории сопоставляется свой выход, а ответом сети считается та категория, на чьем выходе уровень сигнала максимален. В определенном смысле уровень сигнала на выходе "А" - это достоверность того, что на вход была подана рукописная буква "A". Задачи, в которых нужно отнести входные данные к одной из известных категорий, называются задачами классификации. Изложенный подход - стандартный способ классификации с помощью нейронных сетей.

Табл.2. Задача распознавания рукописных букв в терминах нейросети

Задача распознавания рукописных букв
Дано: растровое черно-белое изображение буквы размером 30x30 пикселов	Надо: определить, какая это буква (в алфавите 33 буквы)
Формулировка для нейросети
Дано: входной вектор из 900 двоичных символов (900=30x30)	Надо: построить нейросеть с 900 входами и 33 выходами, которые помечены буквами. Если на входе сети - изображение буквы "А", то максимальное значение выходного сигнала достигается на выходе "А". Аналогично сеть работает для всех 33 букв.

Затем можно переходить к следующему вопросу «как строить сеть». Это решается в два этапа:

1) выбор типа (архитектура сети);

2) подбор весов (обучение) сети.

На первом этапе следует выбрать следующее:

· какие нейроны мы хотим использовать (число входов, передаточные функции);

· каким образом следует соединить их между собой;

· что взять в качестве входов и выходов сети.

Лекция 14. НС (продолжение)

Эта задача на первый взгляд кажется необозримой, но необязательно придумывать нейросеть "с нуля" - существует несколько десятков различных нейросетевых архитектур, причем эффективность многих из них доказана математически. Наиболее популярные и изученные архитектуры - это многослойный персептрон, нейросеть с общей регрессией, сети Кохонена и другие. На втором этапе нам следует "обучить" выбранную сеть, то есть подобрать такие значения ее весов, чтобы сеть работала нужным образом. Необученная сеть подобна ребенку - ее можно научить чему угодно. В используемых на практике нейросетях количество весов может составлять несколько десятков тысяч, поэтому обучение - действительно сложный процесс. Для многих архитектур разработаны специальные алгоритмы обучения, которые позволяют настроить веса сети определенным образом. Наиболее популярный из этих алгоритмов - метод обратного распространения ошибки (Error Back Propagation), используемый, например, для обучения персептрона.

В зависимости от функций, выполняемых нейронами в сети, можно выделить три их типа:

1) входные нейроны – на них подается входной вектор, кодирующий входное воздействие или образ внешней среды; вычислительных процедур в этих нейронах не осуществляется, информация передается со входа на выход путем изменения его активации;

2) выходные нейроны – выходные значения которых представляют выход сети;

3) промежуточные нейроны – составляют основу ИНС, преобразования в них выполняются по вышеприведенным формулам.

Выбор структуры ИРС осуществляется в соответствии с особенностями и сложностью задачи. Для решения некоторых отдельных типов задач существуют оптимальные конфигурации. Если же задача не может быть сведена ни к одному из известных типов, разработчику приходится решать проблему синтеза новой конфигурации, причем необходимо руководствоваться следующими принципами:

1) возможности сети возрастают с увеличением числа ячеек сети, плотности связи между ними и числом выделенных слоев;

2) введение обратных связей наряду с увеличением возможностей сети поднимает вопрос о динамической устойчивости сети;

3) сложность алгоритмов функционирования сети (например, введения нескольких типов синапсов) также способствует усилению возможностей сети.

В большинстве случаев оптимальный вариант получается на основе интуитивного подбора, хотя в литературе приведены доказательства того, что для любого алгоритма существует нейронная сеть, которая может его реализовать.

Многие задачи: распознавания образов (зрительных, речевых), управления, прогнозирования, идентификации сложных систем, сводятся к следующей постановке: необходимо построить отображение такое, чтобы в ответ на каждый возможный входной сигнал Х формировался правильный выходной сигнал Y. Отображение задается конечным набором пар («вход», «известный выход»). Число таких пар (обучающих примеров) существенно меньше общего числа возможных сочетаний значений входных и выходных сигналов. Совокупность всех обучающих примеров носит название обучающей выборки.

В задачах разпознавания образов Х – некоторое представление образа (изображение, вектор чисел), Y – номер класса, к которому принадлежит входной образ.

В задачах управления Х – набор контролируемых параметров управляемого объекта, Y – код, определяющий управляющее воздействие, соответствующее текущим значениям контролируемых параметров.

В задачах прогнозирования в качестве входных сигналов используются временные ряды, представляющие значения контролируемых переменных на некотором интервале времени. Выходной сигнал – множество переменных, которое является подмножеством переменных входного сигнала.

Вообще говоря, большая часть прикладных задач может быть сведена к реализации некоторого сложного многомерного функционального преобразования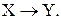

В результате построения такого преобразования (отображения) необходимо добиваться того, чтобы обеспечивалось формирование правильных выходных сигналов в соответствии:

1) со всеми примерами обучающей выборки;

2) со всеми возможными входными сигналами, которые не вошли в обучающую выборку.

Отметим, что теоретической основой для построения НС является следующее утверждение: для любого множества пар входных-выходных векторов произвольной размерности существует двухслойная однородная нейронная сеть с последовательными связями, с сигмоидальными передаточными функциями и с конечным числом нейронов, которая для каждого входного вектора 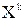формирует соответствующий ему выходной вектор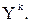

Таким образом, для представления многомерных функций многих переменных может быть использована однородная нейронная сеть, имеющая всего один скрытый слой, с сигмоидальными передаточными функциями нейронов.

Для оценки числа нейронов в скрытых слоях ОНС можно воспользоваться формулой для оценки необходимого числа синаптических весов (в многослойной сети с сигмоидальными передаточными функциями):

где n – размерность входного сигнала, m –размерность выходного сигнала, N – число элементов обучающей выборки.

Число нейронов в двухслойной сети составит: 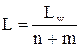или

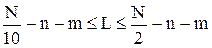
Теорема о полноте. Любая непрерывная функция на замкнутом ограниченном множестве может быть равномерно приближена функциями, вычисляемыми нейронными сетями, если функция активации нейрона дважды непрерывно дифференцируема и нелинейна.

Таким образом, НС являются универсальными аппроксимирующими системами.

Задавшись определенной структурой ИНС, отвечающей какой-либо задаче, разработчик сети должен найти оптимальные значения всех весовых коэффициентов. Этот этап называется обучением ИНС.

Дата добавления: 2014-01-07