Лекция 15. Алгоритмы обучения нейронных сетей

Рассмотрим идею одного из самых распространенных алгоритмов обучения – алгоритма обратного распространения ошибки. Это итеративный градиентный алгоритм обучения, который используется с целью минимизации среднеквадратичного отклонения текущего выхода от желаемого выхода в многослойных нейронных сетях. Этот алгоритм используется для обучения многослойных НС с последовательными связями вида рис.25. Нейроны в таких сетях делятся на группы с общим входным сигналом - слои. На каждый нейрон первого слоя подаются все элементы внешнего входного сигнала. Все выходы нейронов m-го слоя подаются на каждый нейрон слоя m+1. Нейроны выполняют взвешенное суммирование элементов входных сигналов. К сумме элементов входных сигналов, помноженных на соответствующие синаптические веса, прибавляется смещение нейрона. Над результатом суммирования выполняется нелинейное преобразование - функция активации (передаточная функция). Значение функции активации есть выход нейрона.

В многослойных сетях оптимальные выходные значения нейронов всех слоев, кроме последнего, как правило, неизвестны, и трех- или более слойный персептрон уже невозможно обучить, руководствуясь только величинами ошибок на выходах НС. Наиболее приемлемым вариантом обучения в таких условиях оказался градиентный метод поиска минимума функции ошибки с рассмотрением сигналов ошибки от выходов НС к ее входам, т.е. в направлении, обратном прямому распространению сигналов в обычном режиме работы. Этот алгоритм обучения НС получил название процедуры обратного распространения.

В данном алгоритме функции ошибки представляют собой сумму квадратов рассогласования (ошибки) желаемого выхода сети и реального. При вычислении элементов вектора градиента использован своеобразный вид производных функций активации сигмоидного типа. Алгоритм действует циклически и его циклы принято называть эпохами. На каждом этапе на вход сети поочередно подаются все обучающие наблюдения, выходные значения сети сравниваются с целевыми значениями и вычисляется ошибка. Значение ошибки, а также градиента поверхности ошибок используется для корректировки весов, после чего все действия повторяются. Начальная конфигурация сети выбирается случайным образом, и процесс обучения прекращается либо когда пройдено определенное количество эпох, либо когда ошибка достигнет некоторого определенного уровня малости, либо когда ошибка перестанет уменьшаться.

Обучение сети методом ОРО включает в себя три этапа:

· Прямое распространение входного обучающего образа

· Вычисление ошибки и ее обратное распространение

· Регулирование весов

Этот метод основан на вычислении вектора градиента поверхности ошибок, который указывает направление кратчайшего спуска по поверхности из данной точки. Последовательность шагов приводит после ряда итераций к минимуму поверхности ошибок. Основная трудность здесь представляет выбор длины шага. На практике величина шага принимается пропорциональной крутизне склона с постоянной, называемой скоростью обучения. Рассмотрим алгоритм для многослойного прямонаправленного персептрона (МПП) (рис.27).

Рис. 27. Схема трехслойного персептрона

Обозначим через 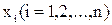входные нейроны; 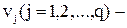нейроны скрытого слоя; 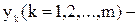выходные нейроны; веса от ячеек входного слоя к нейронам скрытого слоя; 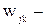веса от нейронов скрытого слоя к выходным нейронам. Индексом р 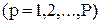обозначим различные образы, предъявляемые на вход. Входные сигналы могут быть бинарными, биполярными или непрерывными.

Поведение сети определяется на основе ряда пар «вход-выход». Каждый обучающий пример состоит из n входных сигналов 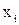и m требуемых выходных сигналов 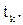Обучение МПП для конкретной задачи эквивалентно нахождению таких значений всех синаптических весов, при которых для соответствующего входа формируется требуемый выход или обучение многослойной сети заключается в регулировании всех весов таким образом, что ошибка между требуемыми выходными 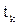и действительными выходными 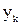сигналами, усредненная по всем обучающим примерам, была минимальна. При предъявлении образа р на вход сети скрытая ячейка j принимает сигнал:

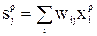
и на своем выходе с помощью функции активации вырабатывает такой сигнал:

Выходная ячейка с номером суммирует сигналы от нейронов скрытого слоя, образуя сигнал, равный:

и после воздействия функции активации формирует выходной сигнал (пороговые значения отброшены, т.к. они всегда могут быть введены в сеть):

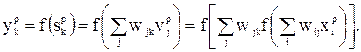
В качестве функции ошибок примем функцию вида:

где требуемое значение выхода.

Подставляя в последнее выражение значение для 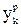, получим:

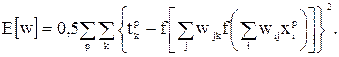
Функция 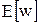является непрерывно дифференцируемой функцией от каждого веса, входящего в него выражения, поэтому можно воспользоваться алгоритмом градиентного спуска для нахождения весов.

Для весов между скрытым и выходными слоями правило градиентного спуска дает:

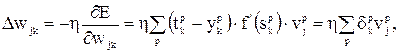
где , 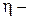коэффициент скорости обучения ().

Для весов между входным и скрытым слоями нужно продифференцировать выражение для 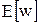, воспользовавшись цепным правилом:

где

Отметим, что уравнения для и 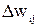имеют одинаковую форму, но различаются значениями параметра 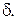В общем случае при произвольном числе слоев правило изменения весов в методе ОРО имеет вид:

где суммирование производится по всем предъявляемым образам; выход и вход относятся к двум концам и 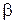синаптического соединения; 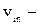активация от скрытой ячейки или реального входы. Значения зависят от рассматриваемого слоя; для последнего слоя эта величина определяется по выражению , а для других слоев – формулой подобной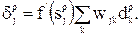

Выражения, определяющие правила изменения весов, записаны в виде сумм по предъявляемым образам, однако обычно образы поступают на вход последовательно: образ р предъявляется на вход, и по окончании прохода «вперед-назад» по сети все веса изменяются перед предъявлянием следующего образа. Это уменьшает функцию ошибок Е на каждом шаге. Если образы выбираются в случайном порядке, то движение по пространству весов происходит стохастически, что позволяет более широко исследовать поверхность ошибок. Альтернативная версия изменения весов (групповое обучение) заключается в минимизации функции ошибки таким образом, что весовые изменения накапливаются по всем обучающим примерам и только затем происходит модификация весов.

Этот алгоритм представляет собой следующую последовательность шагов.

1. Инициировать веса, приняв их малыми случайными величинами.

2. Если условие остановки не выполняется, делать шаги 3-10.

3. Выбирается очередная обучающая пара из обучающего множества; вектор Х подается на вход сети. Для каждой обучающей пары выполнять шаги 4-9.

Дата добавления: 2014-01-07