
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема: Понятие Эпсилон окружности точки
|
|
|
|
1) На числовой прямой.
Эпсон окрестностью точки 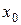 на прямой называется отрезок длины 2
на прямой называется отрезок длины 2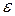 в точке с центром
в точке с центром 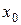 без его граничных точек
без его граничных точек
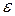
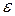
 |
x0 -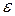 x x0 x0+
x x0 x0+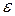
Число 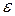 называется радиус окрестности.
называется радиус окрестности.
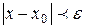 условие принадлежности точки
условие принадлежности точки 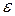 окрестности точки
окрестности точки 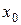
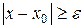 условие не принадлежности точки
условие не принадлежности точки 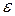 окрестности точки
окрестности точки 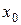
2) на плоскости
 |
y

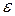 M0
M0
 | |||
 |
0 x
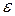 окрестности точки М0 на плоскости называется открытый круг R-
окрестности точки М0 на плоскости называется открытый круг R-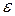 c центром в этой точке
c центром в этой точке
Открытый круг – круг без точек окружности его ограничивающих.
Условия принадлежности и не принадлежности
|
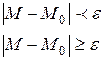
|
3) в пространстве
Рассмотрим ПДСК в пространстве
 z
z
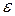


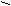

 M0
M0
 |
0 y
x
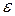 окрестность М0 в пространстве называется отrрытый шар R-
окрестность М0 в пространстве называется отrрытый шар R-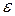 c центром в этой точке.
c центром в этой точке.
Условие принадлежности
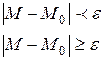
Тема: Предел последовательности (числовой)
Пусть дана 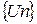
Число, а называется пределом числовой последовательности, если для любого положительного малого заранее заданного числа 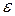 существует № члена последнего, начиная с которого будет выполняться неравенство:
существует № члена последнего, начиная с которого будет выполняться неравенство:
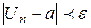
Смысл определения
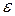 1
1 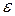 2
2
 |
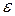 3 а
3 а

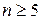
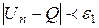



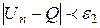

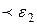

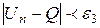
Вывод: Число, а только тогда может называться пределом числовой последовательности, если факт попадания членов последовательности, начиная с некоторого номера (своего для каждой окрестности) в 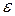 окрестность точки а справедлив для любой заранее заданной и сколь угодно малой окрестности.
окрестность точки а справедлив для любой заранее заданной и сколь угодно малой окрестности.

Докажем, что предел этой числовой последовательности равен 0
Lim Un=Q
n

|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1493; Нарушение авторских прав?; Мы поможем в написании вашей работы!