III. Экономико-математические методы изучения межотраслевых связей

Методом конечного использования.

ВВП = конечное потребление + валовое накопление + сальдо экспорта-импорта):

у₁ + у₂ = ВВП (3)

Данные МОБ применяют при экономико-математических методах исследования межотраслевых связей.

Количественное выражение экономических связей каждой отрасли с другими отраслями может быть представлено в виде системы линейных уравнений.

Таблица 5

Математическая схема МОБ.

	Промежуточное потребление	Конечное использование	Всего использование
	…	j	…	n
Промежуточ. Потребление (отрасли)			…		…
…	…	...	…	…	…	…	…
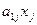
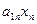
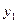
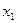
i		…		…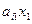
…	…	…	…	…	…	…	…
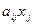
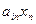
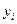
n		…		…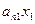
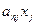
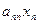
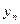
ВДС		…		…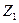
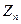
Всего ресурсов		…		…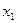

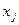
1. Если рассматривать данные МОБ по строкам, то каждую отрасль можно описать в виде следующего уравнения:

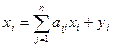
х_i – продукция i-той отрасли;

а_ij – коэффициент прямых затрат продукции i-й отрасли на единицу j-й отрасли; а_ij = х_ij / х_j

х_j – продукция j-й отрасли;

у_i – конечный спрос i-й отрасли (конечное использование)

Данное уравнение характеризует использование продукции каждой отрасли на промежуточное и конечное потребление, накопление и другие нужды.

2. При рассмотрении МОБ по колонкам каждая отрасль может быть представлена уравнением:

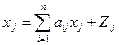
х_j – продукция j-й отрасли;

z_j – валовая добавленная стоимость j-й отрасли.

Уравнение характеризует стоимостной состав выпуска продукции каждой отрасли.

Если представить в матричной форме первое уравнение, то получим:

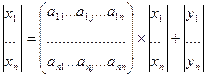или X = AX + Y

Х – вектор выпуска продукции;

A – матрица коэффициентов прямых затрат, позволяющая установить прямые производственные связи между отраслями.

Y – вектор конечного спроса.

С помощью ЭВМ на основе этой матрицы рассчитывается матрица коэффициентов полных затрат, показывающих как прямые, так и косвенные затраты на производство единицы конечной продукции.

Если коэффициенты полных затрат умножить на вектор конечного спроса, то можно получить выпуск продукции по каждой отрасли.

Из формулы X = AX + Y получим Y = X – AX или Y = (E – A) ^х X

Е – единичная матрица.

Далее:

Х = Y × (Е – А) ^–1

(Е – А) ^–1 – матрица коэффициентов полных затрат.

Это основное уравнение МОБ.

Оно применяется главным образом для прогнозирования.

Имея матрицу коэффициентов полных затрат и перебирая различные варианты вектора распределения конечного спроса, можно рассчитать различные варианты прогноза.

Дата добавления: 2014-01-07