Понятие линейного пространства

Рассмотрим множество V элементов x, y, z … и множество всех действительных чисел R. Пусть задан закон, по которому каждой паре x, y элементов множества V ставится в соответствие элемент этого же множества.

Определение 1. Элемент z называют суммой и пишут z = x + y.

Кроме того, пусть задана операция умножения на число, т.е. каждому элементу x и числу ставится в соответствие элемент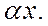

Допустим, что для введённых операций выполняются следующие аксиомы:

1. .

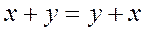
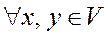2.

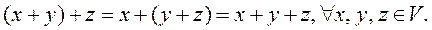
3. В множестве V существует элемент (который называется нулевым и обозначается 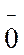) такой, что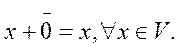

4. Для каждого элемента 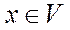существует элемент (который обозначим -x и назовём противоположным x) такой, что .

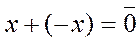5. Для любого .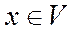

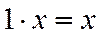Для любых чисел 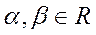и любых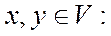

6. .

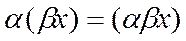7.

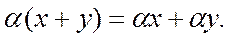
8.

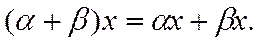
Определение 2.Множество V с операцией сложения и умножения на число, удовлетворяющее указанным аксиомам, называется вещественным линейным пространством. Такое множество V также называют векторным пространством. Элементы из V называются векторами.

Из определения 2 линейного пространства следуют следующие утверждения:

1. В линейном пространстве существует единственный нулевой вектор.

2. В линейном пространстве для каждого вектора x существует единственный противоположный – x.

3. Для элемента – x противоположным будет x.

4. Произведение числа 0 на любой элемент x есть нулевой элемент.

5. Произведение 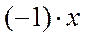равно элементу .

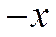6. Произведение любого числа 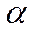на нулевой элемент есть нулевой элемент.

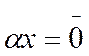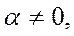7. Если и то .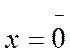

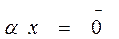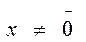8. Если и , то .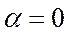

Пример 1.Пусть 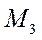– множество свободных векторов. Свободный
вектор - это класс равных между собой векторов, называемых его представителями. Для операций сложения и умножения на число берутся представители классов. Эти операции удовлетворяют аксиомам 1-8, следовательно, 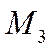является вещественным линейным пространством.

Пример 2.Пусть 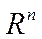– множество, элементами которого являются все возможные упорядоченные наборы n вещественных чисел . Определим сложение и умножение на число:

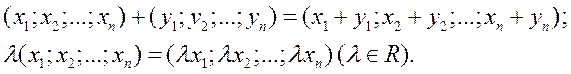
Аксиомы 1-8 выполняются. Значит, множество 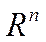с введёнными операциями является линейным пространством.

Пример 3.Рассмотрим множество всех вещественных матриц размеров 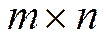, которое обозначим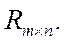

Операции сложения и умножения на число были введены в лекции 4. Эти операции удовлетворяют аксиомам 1-8, значит, множество 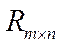с этими операциями является вещественным линейным пространством.

Определение 3.Множество V₁ элементов линейного пространства V называется подпространством пространства V, если выполняются следующие условия:

1.В множестве V₁ операции сложения и умножения на число определяются так же, как в пространстве V.

2.Если 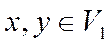, то .

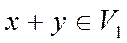3. Если 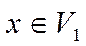, то .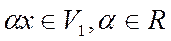

Легко убедиться в том, что всякое подпространство V₁ в свою очередь является линейным пространством, т. е. для V₁ выполняются аксиомы 1-8.

Пример 4.Если в 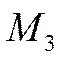из примера 1 рассмотреть множество 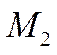векторов, параллельных некоторой плоскости, то 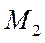будет подпространством .

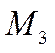Дата добавления: 2014-01-07