Кіріспе 5 страница

Жалпы түрде сызықты жүйені (немесе сызықты арна) екі аргументтің кездейсоқ функциясын көрсететін, кездейсоқ ИХ G(t,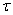) түрінде бейнелеуге болады t (реакцияның бақылану уақытынан) және (тізбектің кірісіне d импульсін бергеннен бастап кеткен уақыт). Мысалы, параметрлері кездейсоқ ішкі әсерлерге ықпал ететін, кез-келген сызықты жүйенің, мысалы температура, қысым, ылғалдылық және т.б. кездейсоқ сызықты арнаны 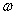және t айнымалыларының кездейсоқ беріліс функциясымен сипаттауға болады

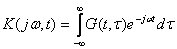. (11.1)

(11.1) сипаттамасы бар кездейсоқ арнаның мағынасындағы Y(t) процесінің корреляция функциясын, X(t) стационарлы.

Процестің кірісіне бергенде, былай анықталады

. (11.2)

мұнда, кездейсоқ арнаның жүйелік сипаттамасы.

Енді, көп кездесетін модельдерге кеңінен тоқталайық. Кездейсоқ кіріс X(t) -ға әсер етуге арналған модель.

, (11.3)

Мұнда, t және g параметрлері флуктурленеді. Қарапайым жағдайда, сымды өткізгіш байланыста осындай флуктуациялар сыртқы шарттың өзгеруінен болады және қатысты кіші аралықта өте баяу жүреді.Толқынның көпсәулелі таралуы кезіндегі радиоарналарда, гидроакустикалық арналарда және де басқаларында флуктуация өте айқын көрінеді.

Сигнал арнаның кірісінен шығысына || жолмен өткенде, күрделі жағдай орын алады. 11.1 суретте әрбір жолдың шығысында сигнал мына түрге ие болады.

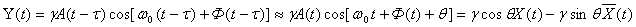мұнда 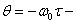арнадағы фазалық ығысу, ал 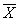(t) мен X(t) Гильберт бойынша түйіндескен процес, бірақ g және t әртүрлі жылдар үшін өзгеше, сонымен қатар аз аралықты флуктурлайды. Мұндай түрдегі сигналдың көпжолды таралуы радио, гидроакустикалық және басқа да арналарға тән.(соның ішінде өткізгіштер).

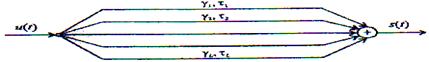
11.1 Сурет - Сигналдың көпжолды таралуы

Әдетте, толқын энергиясы біртексіз ортада таралады және әртүрлі біртексіздіктен шағылады. Бұл біртексіздік кішкене шағылдырушы (шашырау) көлемнің ішінде таралуы мүмкін. Бұл жағдайда және жолдар үшін жүрістің айырмасы [ t мәнінің айырымы] үлкен емес. Егер осындай арнамен өте қысқа импульс жіберетін болса, онда оның шығысындағы импульс қысқа болады. Бұндай арнаны бір сәулелі деп атайды. Бұл жағдайда уақыт бойынша шашырауды (созылуды) тудырмайды, бірақ арнаның беріліс (мультипликативті бөгеуін) функциясының өте тез кездейсоқ өзгерісіне қатысты, тыну құбылысына әкеліп соқтырады.

Тынуы бар бір сәулелі арнаға таржолақты сигнал берілсе, сәуле алдындағы кешігуінің орта квадратты ауытқуы мына шартты қанағаттандырады.

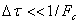, (11.4)

мұнда F_c сигналдық спектр ені, онда сигналдық спектріндегі әртүрлі 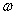жиіліктегі бастапқы фазаның өзгерісі әртүрлі 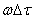немесе бірдей. Сонымен қатар сигнал спектрінің барлық құраушылары бірге тынады, яғни олардың амплитудалары және фазалары бірдей өзгереді. Мұндай тыну ортақ немесе тегіс деп аталады. Егер (11.4) шарты орындалмаса, сигнал спектрінің әртүрлі ауданындағы тыну процесі сәйкес келмейді (жиілік бойынша селективті тыну). Сонда радиобайланыстың көп сәулелі арналарына тән, сигналдық формасының өзгерісі байқалады (кеңістікте шашыраған объектілердің шағылуынан пайда болған сигналдың қабылдау нүктесіне келуі). Байналыс арналарындағы аддитивті бөгеуілдер әрқилы себептерге қатысты туындайды және ескеруге қиын жеке іске асатын әр алуан түрді қабылдауы да мүмкін. Дәл осы бөгеуілдер берілген сигналдың ескеруге тұрмайтын туындысын шақыртады. Әртүрлілігіне қарамайтын электрлік және статистикалық құрылымына қатысты аддитивті бөгеуілдерді 3 негізгі топқа бөледі. Флуктуациялық жиілік және уақыт бойынша бөліну, жиілік бойынша топталған және уақыт бойынша топталған импульсті. Физикалық тұрғыдан, аддитивті флуктуациялық бөгеуілдер әртүрлі топтағы флуктуациялық жүйелерде туындайды, яғни сол немесе басқа физикалық мәндердің параметрлердің олардың орта мәндерінен кездейсоқ ауытқуынан туындауы заряд тасушылардың дискретті табиғатымен шарттасқан электрлік тізбекте шудың көзі ток флуктуациясы болуы мүмкін. Электр тоғының дискретті табиғаты бөлшектік эффект түріндегі жартылай өткізгішті аспаптарда туындайды (берілген схеманың қоректену режимінде туындаған заряд тасушылардың саны өзгереді). Егер екенін ескерсек, 1Гц жиілік жолағына келетін, флуктуациялық тоқтың үлес дисперсиясы

N₀=2eI₀. (11.5)

Радиотехникада бұл қатынас Шоткин формуласы деп аталады. Осы қатынасқа сәйкес, электронды аспаптың балама шулы сұлбасы N₀ жазықтықты спектрі бар ақ шу туғызатын ток көзін сақтайды. Электронды аспаптардың бөлшектік шуында бірнеше жүздеген мегагерцке дейінгі жиілікті тұрақты спектр қуаты болады, ал одан кейін жиіліктің өсуіне сәйкес кішірейеді. Байланыс құрылғыларындағы шудың таралуының себебі флуктуация болып табылады [жылулық қозғалысқа негізделген] заряд тасушылардың бей-берекет жылулық қозғалысына байланысты өткізгіш денелердегі резистор элкетр зарядының көлемдік жазықтығы флуктуациясы шудың пайда болуының ең басты себебі болып табылады. Заряд тасушылардың кездейсоқ жылулық қозғалысы кез-келген өткізгіште соңына қарай потенциалдарың кездейсоқ айырымын тудырады. Мұндай кернеудің орта мәні нольге тең, ал айнымалы құраушысы шуға айналады. Қабылдағыштың кірісінде жылулық шу-орташа нольді кездейсоқ гаустық процесті және қуаттың жазықтық спектрін-Найквист формуласын көрсетеді.

No = 2Wo = 4kTR. (11.6)

Жартылай өткізгіш аспаптар үшін сипаттама болып, аса жоғарғы құбылыстардың әртүрлі тобының қорытындысында туындайтын фликер-шу есептеледі. Жиіліктің кең диапозынындағы спектрлі жазықтығы гиперболоидтық заңға бағынады (1/f пропорционал). Қарапайым жағдайда жиіліктен жоғарғы фликер шуды елемейді. Күннің радиошағылуы және басқа да ғарыштық обьектілерінің әсерінен туатын радиобайланыс жүйесіндегі ғарыштық бөгеуілдер-флуктуациялық шу болып табылады. Радиотехникалық құрылғыдағы шудың көзі. Шығысында электромагниттік өрістің бей-берекет флуктуациясы әсерінен кездейсоқ кернеу туындайтын қабылдау антеннасы болуы мүмкін. Антеннаның шығысындағы, толқынның ұзындығымен салыстырғында кішірек кернеу пайда болады и = El. Егер жердегі табиғи бөгеуілдерді айтсақ, онда бұл шудың қуатты беру белгілі 30 МГц жиіліктен төмен болады. Спектр бойынша жинақталған аддитивті бөгеуілдерге басқа радиостанцияның сигналдарын арнаулы бөгеуілдер, әртүрлі негіздегі жоғарғы жиілікті генератордың сәуле шығаруын (өнеркәсіптік, медициналық) және т.б. жатқызуға болады. Жалпы жағдайда бұл модулденген тербеліс, яғни өзгеретін параметрлері бар квази гармоникалық тербеліс. Бір жағдайларда бұл тербелістер үздіксіз болады (мысалы, тарату және теледидарлық радиостанцияның сигналдары), ал басқа жағдайда олар импульстік сипаттамаға ие (радиотелеграфты станцияның және мәліміттерді беру жүйесінің сигналдары). Жинақталған бөгеулдердің спектр ені көп жағдайда қабылдағыштың өткізу жолағын үлкейтпейді, ал кейде ол жолақтан тар болады. Жайылуы пайдалы сигналдағы сияқты, байланыс сапасын анықтаушы, және флуктуация фазасы және амплитудасының кездейсоқ тербелісі болып табылатын, спектр бойынша жинақталған қысқа толқындардың диапазонындағы бөгеуілдер негізі болып табылады. Импульсті (уақыт бойынша жинақталған) аддитивті бөгеуілдерге жалғыз импульс түріндегі бөгеулдерді жатқызады. Мұнда, үлкен уақыт аралығында бірінен соң бірі, тізбектелген қабылдағыштағы өтпелі құбылыс бір импульсте келесі импульстің келуіне орай сөнеді. Мұндай бөгеуілдерге атмосфералық және индустриалды бөгеуілдерді жатқызады. Егер байқайтын болсақ, ”флуктуациалық бөгеуілдер” және “импульсті бөгеуілдер” өте ұқсас түсініктер. Импульстердің жиілігінің ізділігіне байланысты бірдей бөгеуілдер, кең жолақты өткізгішті қабылдағышқа импульсті сияқты, ал қатысты тар жолақты өткізгішті қабылдағышқа флуктуациялық сияқты әсер етеді. Тәжірибеде импульсті бөгеуілдерді кездейсоқ, қатысты кең жолақты процес ретінде қарастырсақ (кең болған сайын, импульсті бөгеуілдер қысқа) жеке аз, уақыт және амплитуда бойынша кездейсоқ таралған импульстерден тұрады. Мұндай бөгеуілдердің ықтималдылығы, импульстердің амплитудасының таралу ықтималдылығы және Пуассон моделі көмегімен, осы импульстердің аралығындағы уақыттық интервалдардың таралуымен сипатталады. Анодқа 1c келген электрондардың орта санын ν-деп белгілейді. Анодқа келу ықтималдылығы n электронға тең.

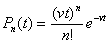. (11.7)

Бұл заңға импульсті бөгеуілдердің нақты моделіне сәйкес келетін, үлкен амплитуда ауданында маңызды мәннің бар болуы сипат. Радиосигналдардың амплитудасының жәй флуктуациясы (тәуліктік, мезгілдік) интерференциялық емес құбылыстарға, ал таралу ортасында сигналдың жұтылуына негізделген.

12 Дәріс. Байланыс арналарының математикалық модельдері

Дәрістің мазмұны:

-аддитивтік, гаусстық шулық арна. Аддитивтік гаусстық шумен және сигналдың анықталмаған фазасымен арна. Дискретті байланыс арналарының моделдері.

Дәрістің мақсаты:

-арнаның математикалық бейнесін беру.

Әдетте кез келген нақты арнаның нақты математикалық бейнесін беру қиын. Оның орнына қысқартылған математикалық модельдер қолданады, олар нақты арнаның барлық маңызды заңдылықтарын шығаруға мүмкіндік береді. Егер байланыс кірісіне аз әсер ететін модельдерді тұрғызу кезінде каналдық ерекшеліктері ескеріліп және екінші ретте детальдары тасталған болса.

Қарапайым және кең қолданылатын арналардың математикалық модельдерін қарастырайық. Себебі олар көбінесе дискретті арналардың сипаттамаларын анықтайтын болғандықтан, үзіліссіз арналардан бастайық.

Арнаның шығысындағы аддитивтік гаусстық шулық сигнал

Z(t) = у u(t - 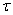) + N(t) = s(t) + N(t), (12.1)

бұл жерде N(f)-нөлдік математикалық күтіліммен және корреляциялық функциямен берілген гаусстық аддитивтік шу. Көбінесе ақ гаусстық шу (БГШ) қарастырылады немесе квази ақ (S(t) сигнал спектрінің жолағында бірқалыпты спектралды тығыздықпен). Жиі талдау кезінде t ескермесе болады, ол арна шығысындағы бастапқы уақыт есептеу өзгерісіне сәйкес келеді. Егер тарату коэффициенті g және t кешігуді белгілі уақыт функцияларымен есептесек, (12.1) моделінің қиындатылған түрі алынады.

Z(t)=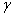(t)u[t-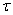(t)]+N(t).

Мұндай модель қанағаттанарлық көптеген өткізу арналарын бейнелейді, тура көріну аралығындағы байланыстағы радиоарналар, сонымен қатар жай жалпы қатаюлармен радиоарналар, ол кезде g және t мәндерін нақты болжауға болады.

Арналық анықталмаған сигналдың фазасымен және аддитивті гаусстық шумен моделінің (12.1) моделінен айырмашылығы, онда кешігу кездейсоқ шама болып табылады. Тар жолақты сигналдар үшін (12.1) өрнегін тұрақты және g кездейсоқ t кезіндегі мына түрде жазуға болады:

,

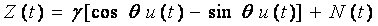бұл жерде 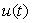--дан Гильберт түрлендірілуі; 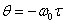-кездейсоқ шама ықтималдық таралуы берілгенмен болжанады, көбінесе 0 ден 2π бірқалыпты интервалында. Егер сигнал фазасы оларда күлтілдесе, бұл модель қанағаттанарлық түрде алдыңғы арналарды да сипаттайды. Орта сигнал қасиеті өтетін, сонымен қатар тіректі генераторлардың фазалық тұрақсыздығынан, мұндай күлтілдеу арнаның тартылуының өзгерісі әсерінен болады.

Сонымен қатар бір сәулелік гаусстық арна ортақ қатаюмен (амплитудалар күлтілдеуі және сигнал фазалары) (12.1) –өрнегімен сипатталады, бірақ 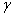көбейткіші, 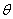фаза сияқты, кездейсоқ процесс деп есептеледі. Басқаша айтқанда, кездейсоқ болып квадраттық компоненттер есептеледі .

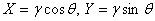Квадратуралық компоненттердің өзгеруі кезінде уақыт бойынша қабылданатын тербеліс

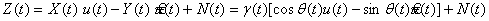. (12.2)

Жоғарыда айтылғандай, бірқалыпты арна тарату коэффициентінің таралуы релелік немесе жалпыланған релелік бола алады. Мұндай арналар сәйкесінше рэлелік немесе жалпыланған рэлелік қатаюмен арналар деп аталады. Арнаның жалпы гаусстық моделінде γ -ң төрт параметрлік жайылуы болады. Қатаюмен бірсәулелік арнаның моделі әртүрлі толқын диапазондарында радиобайланыс арналарын сипаттайды.

Көпсәулелік гаусстық арна жиілік бойынша қатаюмен іріктелген (12.2) моделін жалпылайды:

, (12.3)

бұл жерде N -арнадағы сәулелер саны; 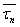- n-ші сәуле үшін орташа уақыт кідірісі. Көпсәулелік ортақ гаусстық модель көптеген радиобайланыс арналарын жақсы сипаттайды. Егер Δτ -ды сәулелер арасындағы кешігу деп есептесек, (12.3) моделі үшін (11.4) шарты орындалмайды.

Дискретті арнаның ішінде әрқашанда үздіксіз арна болады. Үзіліссіз арнаны дискретті арнаға айналдыратын – модем. Сондықтан да берілген модемде үзіліссіз арнаның модельдерінен дискретті арнаның математикалық моделін шығаруға болады. Мұндай жол жиі жемісті болады, ол күрделі моделдерге алып келеді.

Дискретті арнаның қарапайым моделдерін қарастырайық, құрылу кезінде модемнің және үзіліссіз арнаның қасиеттері ескерілмеген.

Дискретті арнаның моделі оның кірісінде көптеген мүмкін сигналдардың есебінен тұрады және берілген кірісте шығыс сигналының шартты ықтималдықтарының таралуы. Бұл жерде кіріс және шығыс сигналы n кодтық символдардың реті болып табылады. Сондықтан да мүмкін кіріс сигналдарын анықтау үшін m әртүрлі символдарды (код негізі) көрсету жеткілікті, сонымен қатар әр символдың Т тарату ұзақтығы. Көптеген қазіргі заманғы арналарда орындалатындай, Т шамасын барлық символдар үшін бірдей деп есептейік. v = 1/T шамасы уақыт бірлігінде берілетін символ санын анықтайды (техникалық жылдамдық бодпен өлшенеді). Арна кірісіне түскен әрбір символ, шығыста бір символдың пайда болуына себепші болады, сондықтан да арна кірісінде және шығысында техникалық жылдамдық бірдей.

Жалпы жағдайда кез келген n үшін мынадай ықтималдылық болуы қажет, егер арна кірісіне кез келген берілген реттілікті кодтық символдарды бергенде шығыста кейбір кездейсоқ реттілік В^{[ n ]} жүзеге асады. Кодтық символдарды 0-ден m-1-ге дейінгі сандармен белгілейік. Бұл бізге олармен арифметикалық операциялар жасауға мүмкіндік береді. Барлық n-реттіліктер (векторлар), саны m-не тең болатын, n-өлшемді ақырғы векторлық кеңістік тудырады, егер “қосуды” m модулі бойынша разрядтық қосу деп есептесек және скалярға көбейтуді анықтау дұрыс.

Тағы да бір пайдалы анықтауышты енгізейік. Қабылданған және таратылған векторлар арасындағы разряд бойынша айырма қателіктер векторы деп атайық. Бұл мынаны білдіреді, канал арқылы дискретті сигналдың өтуін қателік векторымен кіріс векторының қосылуы деп қарастыруға болады. Қателік векторының дискретті арнадағы рөлі шамамен үзіліссіз арнадағы бөгеуілдің рөлі сияқты. Осылайша, векторлық кеңістіктегі қосындыны қолдана отырып, кез-келген дискретті арнаның моделі үшін келесіні жазуға болады.

.

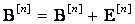бұл жерд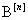е және 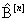- арна кірісіндегі және шығысындағы n символ ішіндегі кездейсоқ реттіліктер; 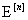- жалпы жағдайда 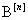тәуелді болатын, кездейсоқ қателік векторы. Егер оның компоненттері 0 және 1 мәндерін қабылдаса онда қателік векторының мағынасы екілік арналар жағдайында (m=2) қарапайым болады. Қателік векторындағы нөлге тең емес символдардың саны оның салмағы деп аталады. Нақтылай айтқанда, модем, бөгеуілдерді және үзіліссіз арнаның тежелуін қателік ағынына түрлендіреді. Ең маңызды және қарапайым дискретті арналардың моделдерін қарастырып өтейік.

Жадысыз симметриялы тұрақты арна дискреттік арна сияқты әрбір берілген кодтық символ p ықтималдылық қателікпен қабылдануы мүмкін және 1-p дұрыс ықтималдылықпен анықталады. Егер қателік болса, берілген символ орнына бірдей ықтималдылықпен кез келген басқа символ қабылдай алады. Осылайша, егер 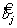беріліп, 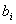символы қабылдау ықтималдылығы

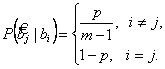(12.4)

“Жадысыз” термині мынаны білдіреді, символдық қателік ықтималдылығы оған дейінгі қандай символдар берілгендігіне және олар қалай қабылданғанша тәуелді емес. Кез-келген n-өлшемді қателік векторының мұндай каналда ықтималдылығы

,

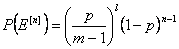бұл жерде l қателік векторындағы нөлге тең емес символдар саны (қателік векторының салмағы). l қателік болғандығының ықтималдылығы, n ұзындығында қалай болса солай орналасқан, Бернулли формуласымен анықталады.

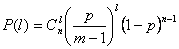^, (12.5)

бұл жерде 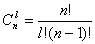биноминалды коэффициент, ол n ұзындық блогындағы әртүрлі қателік байланыстарының санына тең.

Бұл модельді сонымен қатар биноминальды орта деп те атайды.

Модемді нақты анықтағанда пайда болатын арнаны қанағаттанарлықтай сипаттайды. Егер үзіліссіз арнада қатаю болмаса, ал аддитивті шу ақ болса.

Бұл жерде мынаны көру қиын емес, (12.5) моделіне сәйкес p<<1 болғанда ұзындығы n болатын (l >1) екілік кодтық комбинациясының қателігінің пайда болуының ықтималдылығы

.

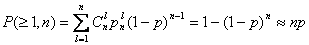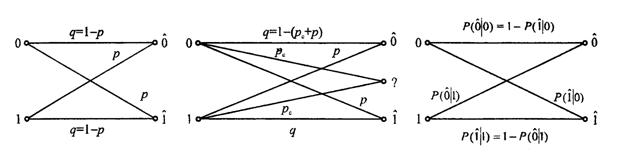
Өтпелі ықтималдықтары екілік симметриялық арнада схемалық түрде 12.1 суретінде көрсетілген.

Жадысыз өшірумен тұрақты симметриялы арна алдыңғысынан айырмашылығы жиі “?” таңбасымен белгіленетін, арна шығысында алфавит қосымша (m+1)-ші символдан тұрады. Бұл символ 1-ші шешуші схема (демодулятор) берілген сигналды сенімді айыра алмаса пайда болады. Мұндай шешімді қабылданбауының немесе p _c символдың өшірілуінің ықтималдылығы бұл моделде тұрақты және берілетін символға тәуелсіз. Өшіруді енгізудің арқасында қателік ықтималдылығын азайтуға мүмкіндік болады, кейде оны нөлге тең деп те есептейді. 12.2 суретте модельдің өтпелі ықтималдықтары схемалық түрде көрсетілген.

Жадысыз симметриялы емес арна алдыңғы модельдер сияқты сипатталады, онда қателіктер бір-біріне тәуелсіз пайда болады, бірақ қателік ықтималдығы қандай символ берілетіндігіне байланысты. Екілік симметриялы емес арнада 1 символын қабылдауының P(1/0) ықтималдылығы 0 символын беру кезінде P(0/1) ықтималдығына тең емес 0 қабылдау 1 беру кезінде (12.3 суретті қара).

Бұл моделде қателік векторының ықтималдылығы қандай символ реттілігі берілетіндігіне тәуелді.

12.1 Сурет - Екілік симметриялы арнадағы өтпелі ықтималдықтары	12.2 Сурет - Өшірумен екілік симметриялық арнадағы өтпелі ықтималдықтар	12.3 Сурет - Екілік симметриялы емес арнадағы өтпелі ықтималдықтар

13 Дәріс. Дискретті-үздіксіз арнаның моделі. Дискретті хабарды алудың ережесі және сапа критериі. Дискретті хабарды беру жүйесінің бөгеуілге тұрақтылық теориясы

Дәрістің мазмұны:

-дискретті-үздіксіз арнаның моделі. Котельников критериі. Толық белгілі сигнал кезіндегі қабылдаудың тиімді алгоритмі (когерентті қабылдау).

Дәрістің мақсаты:

-арнаның математикалық сипаттамасын беру.

b_i тәуелсіз белгісі бар дискретті-үздіксіз арна кірісінде және шығысында Z(t) үздіксіз сигналымен P(b_i) сигналдарының ықтималдығымен және символын беру шарты кезінде Z(t) іске асатын w[] өту жолағымен сипатталады. Бұл жазықтықты шындыққа жақын функция деп атайды. Дискретті-үздіксіз арнаны шындыққа жақын функциясының орнына b_i символын беретін P(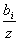) апостериорлы ықтималдығымен сипаттауға болады.

Байес формуласына сәйкес P (),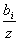

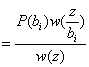мұнда

Дата добавления: 2014-01-07