
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кіріспе 6 страница
|
|
|
|
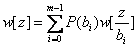 (13.1)
(13.1)
қабылданған тербелістің жазықтығы.
P(bi) - bi cимволын берудің априорлы ықтималдығы яғни, бақылауға және анализге дейін орын алатын ықтималдылық және кодтау ережесімен және хабар көзінің статистикасымен анықталады.
Алдымен кең таралған Котельников критериін немесе идеалды бақылаудың критериін қарастырайық. Соған сәйкес демодулятордың сапасы, символды дұрыс қабылдаудың сөзсіз ықтималдығымен орташа бағаланады. [0,1] кесіндісіндегі демодулятордың кірісіне Z(t) сигналының кейбір элементі келсін. Бұл кезде демодулятор 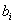 символы берілді деп шешім шығарады, яғни
символы берілді деп шешім шығарады, яғни 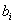 бағасын береді деп тұжырымдаймыз.
бағасын береді деп тұжырымдаймыз.
Бұл шешімнің дұрысытығының ықтималдығы 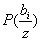 шартының ықтималдығына тең. Z(t) сигналының элементінің іске асуы шарты кезінде
шартының ықтималдығына тең. Z(t) сигналының элементінің іске асуы шарты кезінде 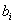 символы шын мәнісінде берілді. Бұны
символы шын мәнісінде берілді. Бұны 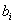 символының апостериолы ықтималдығы деп аталады, яғни сигналын талдағаннан және бақылағанннан кейін жиналған тәжірибеден жинақталған ықтималдылық
символының апостериолы ықтималдығы деп аталады, яғни сигналын талдағаннан және бақылағанннан кейін жиналған тәжірибеден жинақталған ықтималдылық
Басқа сөзбен айтқанда, идеалды бақылаушының критериі, апастериорлы ықтималды максимумның ережесімен тұрғызылған-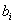 шешуі шешуші схемамен қамтамасыз етіледі.
шешуі шешуші схемамен қамтамасыз етіледі.
Бұл жүйе m теңсіздігінен орындалған жағдайда ғана қолданылады.
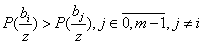 . (13.2)
. (13.2)
Екілік жүйенің сигналдары үшін жоғарыдағы шарт мына теңсіздікті қанағаттандырады.
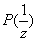
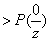 . (13.3)
. (13.3)
(13.3) теңсіздігі орындалса, 1 символы тіркемді, ал керісінші жағдайда – 0 (13.1)-ді (13.2)–ге қойып және w(z)-і функциясы болып табылатындай, ықтималдықтың сөзсіз шарты екенін ескеріп, идеалды бақылаудың критериін өлшеуді былай жазуға болады.
P(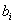 )w(
)w( ) >P(
) >P(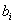 )w(
)w( ), j=0,1,…,m-1,j≠1.
), j=0,1,…,m-1,j≠1.
Бұл алгоритмді іске асыратын қабылдағыш, Котельников қабылдағышы деп аталады. Екілік жүйелер үшін шарт мына теңсіздікті қанағаттандырады.
P(1)w(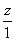 )>P(0)w(
)>P(0)w(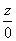 ). (13.4)
). (13.4)
Егер осы шарт орындалса символ тіркеледі, ал орындалса- идеалды бақылау критерий ережесі бойынша шешуші сұлбаны тұрғызу үшін, P(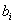 ) символының априорлы ықтималдығын сонымен бірге w[
) символының априорлы ықтималдығын сонымен бірге w[ ], j- шартты жазықтықты анықтайтын-модулятордың және арнаның қасиетін білу қажет.
], j- шартты жазықтықты анықтайтын-модулятордың және арнаның қасиетін білу қажет.
Котельников критериін басқаша да жазуға болады, 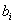 символы берілді және қабылданады, егер j≠1 болса m-1 теңсіздігі
символы берілді және қабылданады, егер j≠1 болса m-1 теңсіздігі
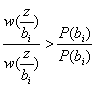 . (13.5)
. (13.5)
Осы теңсіздіктің сол бөлігіндегі қатынас екі гепотездің шындыққа жақын қатынасы деп аталады. Символы және 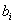 символы берілгендігі туралы оны Λ ij деп белгілейді.
символы берілгендігі туралы оны Λ ij деп белгілейді.
Барлық m символы шындыққа жақын берілген жағдайда, яғни P(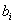 )=
)=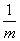 , (13.5) ережесі қысқарады.
, (13.5) ережесі қысқарады.
Λij>1, i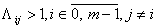 . (13.6)
. (13.6)
Кейде 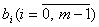 символын беру туралы гипотезді және ешқандай сигнал берілмегені туралы қосымша гипотезаны еңгізеді, яғни Z(t)=n(t) -таза бөгеуіл. Шындыққа жақын қатынасты
символын беру туралы гипотезді және ешқандай сигнал берілмегені туралы қосымша гипотезаны еңгізеді, яғни Z(t)=n(t) -таза бөгеуіл. Шындыққа жақын қатынасты 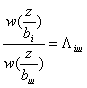 қарапайым түрде Λi деп белгілейді. Сонда (13.6) ережесін мына түрде жазуға болады
қарапайым түрде Λi деп белгілейді. Сонда (13.6) ережесін мына түрде жазуға болады
Λi > Λj барлығы үшін j ≠ i. (13.7)
Шындыққа жақын максималды ережесі, барлық символдар шындыққа жақын берілген жағдайда идеалды бақылаудың критериін іске асырады. Ережесі екілік жүйелер үшін мына теңсіздікті қанағаттандырады
Λ1>Λ 0. (13.8)
Байланыс техникасында, максималды шындыққа жақын (13.7) (13.8) ережесін қанағаттандырады, егер барлық символдар тең ықтималды берілсе, шындыққа жақындықтың максималды ережесі идеалды бақылаудың критериін іске асырады. Дегенмен шешудің бұл ережесін белгілі және белгісіз, бірақ символдардың бірдей априорлы ықтималдылықтарында қолданады. Әрине, ол бұл жағдайда дұрыс қабылдаудың ықтималдығының максимумын қамтамассыз етпейді.
Шешуші сұлбаны, максималды апостериорлы ықтималдылық ережесімен тұрғызылган сұлбамен ауыстырып қате ықтималдылығын азайтуға болар еді. Онда ықтималдылық символдардың қабылдау ауданын кеңейту керек еді. Қорытындысында аз берілетін символдардың көп берілетін символдарға қарағанда сенімділігі төмен.
Бірақ аз берілетін сигналдар, жекеге қарағанда ақпаратты көп тасиды. Сондықтан максималды шындыққа жақын ережесінен максималды апостериорлы ықтималдылығында өту қатенің ықтималдылығын азайтқанмен демодуляция кезінде ақпараттың жоғалуына әкеліп соқтырады.
Арнадағы бұрмалану қатаң түрде детерменирленген және кездейсоқ деп басында ақ деп берілген, спектрлі жазықтығы бар, гаусстың аудитивті ШУА есептеледі. Бұл дегеніміз, символын беру кезінде қабылданған тербелісті мына модельмен сипаттауға болады.
z(t)=si(t)+n(t), 0 ≤ t ≤ T, (13.9)
мұнда барлық белгілі si(t)= γf(t-τ-kT,bk(i)) = γui(t-τ).
Бұл шартта 0….T тактілі интервалында тиімді сигналды талдайтын демодулятор жұмысының алгоритімін анықтайық. Ол үшін нөлдік гипотезаға қатысты барлық мүмкін болатын мәндер үшін шындыққа жақын қатынасты табу керек. Сигнал спектрі енінің шексіздігі, есепті қиындатады. Сондықтан сигналдардың кеңістігі шексіз өлшемді. Бұндай сигналдар үшін (шексіз өлшемді векторлар) ықтималдылық жазықтығы болмайды. Алайда, кез келген сигнал қимасы үшін өлшемді ықтималдылық жазықтығы бар болады. Алғашында ақ шу, кейбір жиілік жолағында болса біржақты спектрлі қуат жазықтығын иеленетін шумен ауыстырайық.
Қосымша гепотезаны қарастырайық, яғни нөлдік стационарлы шу деп есептейік. Интервалында тең тұратын қима арқылы аламыз.
Есептеуі бұл қимада квази ақ гасустік шу үшін тәуелсіз. Символы берілген гипотезаға сәйкес. Ақ шу үшін бастапқы есепке қайта оралайық. Ол үшін F жолағын кеңейтеміз, онда n қиманың саны шексіздікке, ал ∆t –нөлге ұмтылады. Қабылдау ережесі, мына теңсіздік жүйесін тексеруге сәйкес келеді.
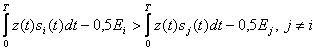 , (13.10)
, (13.10)
мұнда, күтуші сигналының энергиясы теңдігі шығыс тербелістің алдында тиімді қабылдағышты анықтайтын, операцияны анықтайды. (Қабылдау алгоритімі)
Екілік жүйелер үшін алгоритімі бір теңсіздікті тексереді. Теңсіздігі орындалғанда символы тіркеледі, ал қарама-қарсы жағдайда Скаляр туындыны есептейтін қондырғы немесе корреляциялық интеграл активті фильтр немесе коррелятор деп аталады. Сондықтан алгоритімін іске асыратын қабылдағыш, корреляциялық деп аталады.
Суретте қатынасқа сәйкес қабылдағыш құрылғының құрылымдық сұлбасы көрсетілген:
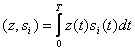 . (13.12)
. (13.12)
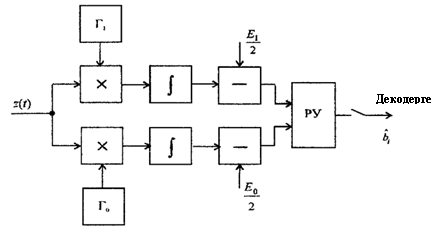
14.1 Сурет - Қабылдағыш құрылғының құрылымдық сұлбасы
Егер сигналдарының іске асуы бірдей энергияға ие болса қабылдау алгоритмі қысқаратылады және мына түрге ие болады (есептеу құрылғысы қажет болмай қалады)
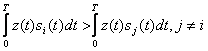 . (13.13)
. (13.13)
Егер демодулятордың кірісіне келетін сигналды кез-келген санға көбейтсек, шешу ережесі өзгермейді. Сигналдың барлық іске асуы тек энергияға ие болатын жүйе және мынасымен ерекшеленеді. Қабылдаудың тиімді алгоритмі онда келген сигналдың масштабын білуді қажет етпейді. Басқаша айтқанда арнаның беру коэффиценті флуктурленіп, тынуы егер арналар үшін маңызды, тең энергиялы сигналдар жүйелерінің кең таралуына себепші болады. Екілік жүйелер үшін теңдеуін қарапайым түрде жазуға болады.
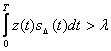 , (13.14)
, (13.14)
мұнда sΔ(t)=s1(t)-s0(t) - әртүрлі жиіліктегі сигнал;
λ = 0,5(E1-E0 ) - табалдырықты деңгей.
Энергиясына тең сигналдар жүйесі үшін. Бұл, сұлбаның іске асуын жеңілдетуі. Іске асыру үшін суреттің сұлбасындағы тек бір ғана тармақ қажет болады.
14 Дәріс. Келісілген фильтрмен тиімді қабылдағыш
Дәріс мазмұны:
-толық белгілі сигналдардағы (когерентті қабылдау) келісілген фильтірге қабылдаудың тиімді алгоритмін жүзеге асыру.
Дәріс мақсаты:
-тиімді демодуляторды синтездеу.
(13.12) скалярлы көбейтіндісін алдыңғы параграфта сипатталған активті фильтрмен ғана емес, сонымен қатар тұрақты параметрлерімен, сызықты фильтр көмегімен де сипатауға болады. Егер фильтр кірісіне Z(t) қабылдау сигналын берсек, онда фильтр шығысындағы кернеу t=T уақыт мезетінде,
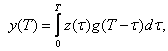
бұл жерде g(τ) -фильтрдің импульстік сипаттамасы. t=T мезетінде y(T) (13.12) скалярлық көбейтіндісіне тең болатындай етіп алайық. Бұл келесі келісіммен болады:
g(T-τ) = si(τ) немесе g(t) = si(T-τ). (14.1)
Жалпы жағдайда S(t) сигналы үшін келісілген фильтрді тұрақты параметрлермен сызықты пассивті фильтр деп атайды және НС
g(t)=as(t0-t), (14.2)
бұл жерде а, t0-тұрақтылар. g(t) функциясы 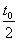 нүктесі арқылы өткізілген оске қатысты айналық бейнесі S(t) болып табылады. Фильтрдің физикалық іске асуы үшін t<0 кезінде g(t)=0 болуы қажетті және жеткілікті. Дербес жағдайда, S(t) сигнал үшін, t=0 мезетінде фильтр кірісіне түсетін және T мезетінде аяқталатын, келісілген фильтрдің физикалық іске асуының шарты орындалады, 14.1-суретінде көрсетілгендей, егер t0 тұрақтысы (санау мезеті) мына шартты қанағаттандырса
нүктесі арқылы өткізілген оске қатысты айналық бейнесі S(t) болып табылады. Фильтрдің физикалық іске асуы үшін t<0 кезінде g(t)=0 болуы қажетті және жеткілікті. Дербес жағдайда, S(t) сигнал үшін, t=0 мезетінде фильтр кірісіне түсетін және T мезетінде аяқталатын, келісілген фильтрдің физикалық іске асуының шарты орындалады, 14.1-суретінде көрсетілгендей, егер t0 тұрақтысы (санау мезеті) мына шартты қанағаттандырса
t0-T ≥ 0 немесе t0 ≥ T.
ИС-мен келісілген фильтрдің беріліс функциясы (жиіліктік сипаттамасы) Фурье түрлендірілуімен анықталады:

14.1 Сурет - S(t) сигналы және g(t) бұл сигналмен келісілген сызықты фильтрдің импульстік сипаттамасы
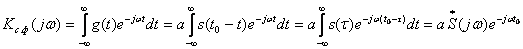 , (14.4)
, (14.4)
Бұл жерде 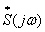 - S(t) сигналдың спектральді тығыздығымен кешенді түйіндескен функция. Осыған сәйкес нақтылықпен дейін АЖС келісілген фильтрдің а коэффициентіне дейін S(t) сигналының амплитудалық спектрімен анықталады (яғни, фильтр сигнал энергиясына үлкен үлес беретін жиіліктерді жақсы жібереді), ал оның фаза жиіліктік сипаттамасы (t0 кідірісімен анықталатын ωt0 - қосылғышын ескермеген жағдайда) сигналының фазалық спектрінің таңбасына қарама-қарсы. Осыған байланысты, t0 мезетінде қабылданатын сигналдың барлық спектр құраушылары фазада жиналады және максималды әсер береді. (14.1) формуласына сәйкес T уақыт мезетінде келісілген фильтр шығысындағы кернеу активті фильтрдің интеграторының шығысындағы сигналға пропорционал 13.1 суретте көрсетілген. Сондықтан да демодулятор, (13.11) алгоритмін жүзеге асыратын келісілген фильтрлер негізінде орындала алады. Мұндай демодулятордың құрылымдық сұлбасы екілік жүйе үшін 14.2 суретте көрсетілген, бұл жерде СФ,- Si(ƒ) сигналымен келісілген фильтр.
- S(t) сигналдың спектральді тығыздығымен кешенді түйіндескен функция. Осыған сәйкес нақтылықпен дейін АЖС келісілген фильтрдің а коэффициентіне дейін S(t) сигналының амплитудалық спектрімен анықталады (яғни, фильтр сигнал энергиясына үлкен үлес беретін жиіліктерді жақсы жібереді), ал оның фаза жиіліктік сипаттамасы (t0 кідірісімен анықталатын ωt0 - қосылғышын ескермеген жағдайда) сигналының фазалық спектрінің таңбасына қарама-қарсы. Осыған байланысты, t0 мезетінде қабылданатын сигналдың барлық спектр құраушылары фазада жиналады және максималды әсер береді. (14.1) формуласына сәйкес T уақыт мезетінде келісілген фильтр шығысындағы кернеу активті фильтрдің интеграторының шығысындағы сигналға пропорционал 13.1 суретте көрсетілген. Сондықтан да демодулятор, (13.11) алгоритмін жүзеге асыратын келісілген фильтрлер негізінде орындала алады. Мұндай демодулятордың құрылымдық сұлбасы екілік жүйе үшін 14.2 суретте көрсетілген, бұл жерде СФ,- Si(ƒ) сигналымен келісілген фильтр.
Келісілген фильтрдің ұзақтығы T болатын финитті сигналға әсер, 0 уақыт мезетінде кіріске берілген, тартылуы 2T болатын финитті интервалда ғана болады. Шынында да, егер фильтр кірісіне сигнал берілсе, онымен келісілген, онда келісілген фильтрдің шығысындағы сигналдық құраушылар:
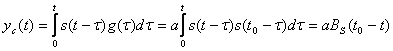 , (14.5)
, (14.5)
бұл жерде Bs{tQ — t} сигналдың S(t) t0 – t аргументінде. Финиттік сигнал үшін ол (0,2T) интервалында анықталған және t=t0=T нүктесінде максимумға ие болады. Келісілген фильтрдің кірісіндегі және шығысындағы пайдалы сигналдың фомасының бір бірінен айырмашылығы бар екендігін сызып көрсетейік. Келісілген фильтрдің есебі шумен тежелген, сигналдың қалпына келмеген формалары болып табылады, ал бір есепті алу ол бойынша белгілі формадағы сигнал фильтрінің кірісінде бар немесе жоқ екендігін болжауға болады.
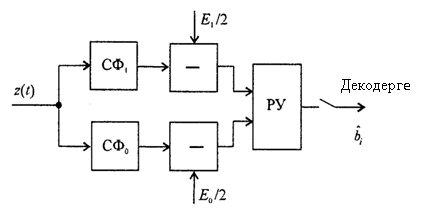
14.2 Сурет
g(t) импульстік сипаттамамен кез келген сызықты тұрақты фильтр өзінің шығысында t0≥T уақыт мезетінде шу дисперсиясына сигналдың пиколық қуатына қатынасы:
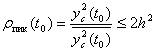 , (14.6)
, (14.6)
бұл жерде 2h2~ келісілген сигналдың pmax(t0) мәні (h2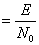 ұзақтығы сигнал энергиясының оң жиіліктердегі шудың спектральды тығызығына қатынасы). Келісілген сүзгілердің жүзеге асу мүмкіндіктерін қарастырайық. Финиттік сигнал үшін еркін S(t) түрдегі келісілген сүзгіні тежелмейтін ұзын жол негізінде тұрғызуға болады, T уақытқа сигнал тежелуін қамтамасыз ететін, шексіз шықпа тығыздығымен. Тәжірибеде ∆
ұзақтығы сигнал энергиясының оң жиіліктердегі шудың спектральды тығызығына қатынасы). Келісілген сүзгілердің жүзеге асу мүмкіндіктерін қарастырайық. Финиттік сигнал үшін еркін S(t) түрдегі келісілген сүзгіні тежелмейтін ұзын жол негізінде тұрғызуға болады, T уақытқа сигнал тежелуін қамтамасыз ететін, шексіз шықпа тығыздығымен. Тәжірибеде ∆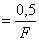 қалыптасуымен дискретті нүктелерде шықпаларды алуға болады, бұл жерде F-сигнал спектрінің тиімді ені.
қалыптасуымен дискретті нүктелерде шықпаларды алуға болады, бұл жерде F-сигнал спектрінің тиімді ені.
Шындығында, 14.3 суретте көрсетілген сұлба арқылы берілген нақтылықпен S(t) кез келген сигналды синтездеуге болады, көрсетілген қисық Котельников қатарымен:
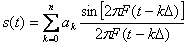 ,
,
мұнда ak=s(kΔ); Δ=1/(2F);
F-сигнал спектрінің ені.
Оның кірісіне 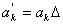 салмақпен ∆ уақыт интервалы арқылы δ - импульс реттілігін бере отырып, мұндай сигналды өткізу жолағы F болатын идеалды ФНЧ(ТЖС) шығысында алуға болады. Бұл суретінің сұлбасындағы әйгілі жақындаумен іске асады. Егер жол кірісіне бастапқы мезетте 1 қысқа импульс берілсе, δ - функциясын аппроксимациялайтын, онда ∆ интервалға таралған дәл осындай шықпалардан импульстер алынады, олар a k тартылған блоктардан өте отырып кезек-кезек ФНЧ (Тжс) кірісіне түседі. Тартылған блоктар аттенюаторлар немесе күшейту коэффициенті | a’k | болатын күшейткіштер, сонымен қатар теріс -инверторлардан тұрады.
салмақпен ∆ уақыт интервалы арқылы δ - импульс реттілігін бере отырып, мұндай сигналды өткізу жолағы F болатын идеалды ФНЧ(ТЖС) шығысында алуға болады. Бұл суретінің сұлбасындағы әйгілі жақындаумен іске асады. Егер жол кірісіне бастапқы мезетте 1 қысқа импульс берілсе, δ - функциясын аппроксимациялайтын, онда ∆ интервалға таралған дәл осындай шықпалардан импульстер алынады, олар a k тартылған блоктардан өте отырып кезек-кезек ФНЧ (Тжс) кірісіне түседі. Тартылған блоктар аттенюаторлар немесе күшейту коэффициенті | a’k | болатын күшейткіштер, сонымен қатар теріс -инверторлардан тұрады.
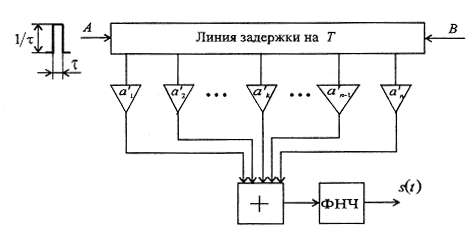
14.3 Сурет
14.3 суреттің сұлбасы импультің реакциясы S(t) болатын трансверсальды деп аталатын сызықты сүзгіні береді. Оңай көруге болады, егер кіріс импульсті А нүктесіне емес, В нүктесіне берсек, онда S(t) айналық бейнесін беретін, сигнал синтезделеді. Сондықтан да сол схема В нүктесінде кіріскен сүзгі болып табылады, S(t)-мен келісілген.
Активті сүзгі кезінде тактілік интервалмен салыстырғанда есеп алудың нақты еместігінің төмен болуы, ал келісілген сүзгі кезінде –радиоимпульсті (когерентті есеп деп аталатын) жоғары жиілікпен толтыру периодымен салыстыруды қажет ету жеткілікті. Келісілген сүзгіде когерентті есептеудің қамтамасыз ету қиындығы, активті сүзгіде когерентті тіректі генераторларды жүзеге асыру қиындығымен бірдей деуге болады.
Келісілген сүзгіге қатысты маңызды бір жағдайды белгілеп қояйық. Оның кірісіне Z(t) тербеліс берілсін, ол сүзгі финиттік сигналмен келісілген болсын. Онда оның шығысында сигнал t уақыт мезетінде
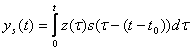 . (14.7)
. (14.7)
Сүзгі шығысында, түйіскен сигналмен келісілген, z(t) тербелісі мынаны береді
 . (14.8)
. (14.8)
(14.7) және (14.8) сигналдары таңбаға дейінгі дәлдікпен Гильберт бойынша түйіскен. Сүзгі шығысындағы орама s(t) сигналымен келісілген.
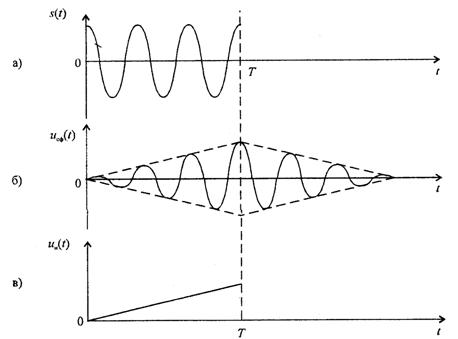
а) кірістегі импульс;
б) келісілген сүзгі шығысындағы импульс;
в) активті сүзгі интеграторының шығысындағы кернеу.
14.4 Сурет -Тікбұрышты радиоимпульс кірісіне бергенде корреляциялық схеманың және келісілген сүзгі шығысындағы сигналдар
15 Дәріс. Тиімді когерентті қабылдаудың бөгеуілге тұрақтылығы. Шеннон теоремасы
Дәрістің мазмұны:
-тиімді когерентті қабылдаудың бөгеуілге тұрақтылығы. Шеннон теоремасы.
Дәрістің мақсаты:
-аддетивті БГШ бар, екілік жүйелер үшін арнадағы потенциалды бөгеуілге тұрақтылықты анықтау, қабылдау кезінде екі күтуші сигнал да анық болса: S1(t) және S0(t), онда бұл сигналдардың априорлы ықшамдылықтары бірдей.
Z(t) келген сигналы кездейсоқ болады. Біріншіден берілген сигналдың іске асуы алдын ала белгісіз, ал екіншіден ол N(t) кездейсоқ бөгеуілін қамтамасыз етеді. Бұл жағдайда (5.26) сәйкес тиімді қабылдаудың алгоритмі
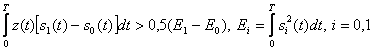 . (15.1)
. (15.1)
(15.1) теңсіздігін орындау кезінде тиімді қабылдағыш S1(t) сигналына сәйкес, 1 символын ал қарама-қарсы жағдайда S0(t), сигналына сәйкес-0 символын тіркейді. Егер шын мәнісінде 1 символы берілсе, онда Z(t)=S1(t)+N(t) қате ықтималдылығы (15.1) теңсіздігінің орындалмау ықтималдылығымен анықталады, яғни кері теңсіздіктің орындалу ықтималдылығымен. Егер –нөлдік орташа және қуатының біржақты спектрлік жазықтығы бар ақ стационарлы шу болса, Q функция арқылы қате ықтималдылығын мына түрде жазуға болады:
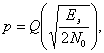 (15.2)
(15.2)
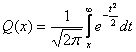 табулирленген және қатенің қосымша функциясы деп аталынады.
табулирленген және қатенің қосымша функциясы деп аталынады.
NQ бөгеуілдің берілген интенсивтілігінде, екілік жүйенің потенциалды бөгеуілге тұрақтылығы сигналдың балама энергиясына ғана тәуелді:
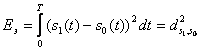 . (15.3)
. (15.3)
Ол Гильберт кеңістігіндегі сигналды нүктелердің ара қашықтығының квадратына тең. Бөгеуілге тұрақтылық пайдаланылатын сигналдардың түріне қатыссыз қолданылатын сигналдардың толығырақ айтсақ, балама энергиясы көп болатын жүйелерде жоғары (қатенің ықтималдылығы аз). Соңғысы, жеке жағдайда оңай да, (аз базалы синусоиданың қиындыларымен) қиын да болуы мүмкін.
15.1 суретте екі өлшемді кеңістікте екілік жүйе үшін сигналдардың нүктесі көрсетілген.
15.1, а сурет- АМ кезінде:
s0(t)=0, 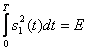 .
.
15.1, б сурет ортогональді сигналы
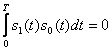 ,
, 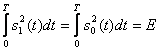
бар жиілік модуляциясы.
15.1, в сурет
s1(t)=-s0(t)
қарама-қарсы сигналы бар. ФМ суретте көрсетілгендей, екілік АМ салыстырғанда екілік ЖМ сигналдың балама энергиясы Eэ=||s1- s0||2 2 есе үлкен, ал екілік ФМ үшін-4 есе үлкен.
(15.3) қатынасы, S1(t) және S0(t) сигналдарының тиімді таңдауын жасауға мүмкіндік береді немесе сигналдың берілген E энергиясында максималды бөгеуілге тұрақтылық мүмкінділік қамтамасыз етеді U1(t) және Y0(t)
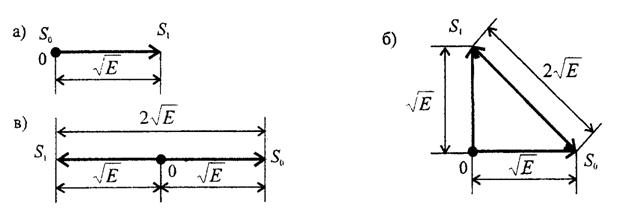
15.1 Сурет - Екі өлшемді кеңістікте екілік жүйе үшін сигналдардың нүктесі
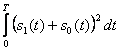 интегралы тек қана теріс емес мәндерді қабылдайды, сондықтан да оның минимумына 0-ге тең және s1(t)=-s0(t) шарты кезінде орындалады. Тұрақты параметрлері екілік жүйеде және аддитивті БГШ кезінде ең тиімді қарама-қарсы сигналды жүйе болып есептеледі. Бұл жүйені мысалға, екі полярлы импульстер және сигналдардың фазасының айырымы ∆φ=π болатын екілік фазалық модуляцияның сигналдары қанағаттандырады. Барлық Eэ=4E сияқты жүйелер үшін және қателіктің ықтималдылығы:
интегралы тек қана теріс емес мәндерді қабылдайды, сондықтан да оның минимумына 0-ге тең және s1(t)=-s0(t) шарты кезінде орындалады. Тұрақты параметрлері екілік жүйеде және аддитивті БГШ кезінде ең тиімді қарама-қарсы сигналды жүйе болып есептеледі. Бұл жүйені мысалға, екі полярлы импульстер және сигналдардың фазасының айырымы ∆φ=π болатын екілік фазалық модуляцияның сигналдары қанағаттандырады. Барлық Eэ=4E сияқты жүйелер үшін және қателіктің ықтималдылығы:
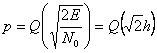 , (15.4)
, (15.4)
мұнда 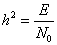
 демодулятордың кірісіндегі сигналдың энергиясының, флуктуациялық бөгеуілдің спектрлі жазықтың қуатына қатынасы.
демодулятордың кірісіндегі сигналдың энергиясының, флуктуациялық бөгеуілдің спектрлі жазықтың қуатына қатынасы.
Энергияға тең ортогональ сигналды жүйе үшін (мысалға екілік жүйесі үшін белгілі шарт кезінде) 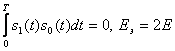 және қателіктің минималды ықтималдылығы болады:
және қателіктің минималды ықтималдылығы болады:
p = Q(h). (15.5)
(15.5) және (15.4) салыстыра келе, мынадай қорытындыға келеміз ортоганальды сигналды жүйеден тиімді жүйеге өту қарастыратын арнада таратқыштың орташа қуаты екі есе азайғанда, байланыстың сапасын тұрақтандырады яғни, екі есе энергиялық ұтыс береді. Бұл қорытындыны 15.1 суреттен де көруге болады. s0(t)=0 және 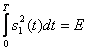 деп есептеп, пассивті үзілісті екілік жүйеде, қатенің минималды ықтималдылығын аламыз:
деп есептеп, пассивті үзілісті екілік жүйеде, қатенің минималды ықтималдылығын аламыз:
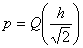 . (15.6)
. (15.6)
Бұл жерден көретініміз, АМ жүйесінен ЖМ жүйесіне өту кезінде максималды қуат бойынша энергиядан ұту екіге тең ал ФМ жүйесіне өту кезінде 4-ке тең.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1008; Нарушение авторских прав?; Мы поможем в написании вашей работы!