Если же, то внешнее поле может перебросить электрон через запрещенную зону и тогда электрон станет свободным. Такие вещества называются полупроводниками

Если ширина запрещенной зоны, то средняя скорость электронов будет равна нулю независимо от того, есть внешнее поле или его нет, поскольку переход из валентной зоны в зону проводимости требует в этом случае значительных энергетических затрат. Такие вещества называются диэлектриками или изоляторами.

Квадрат модуля этой функции не будет зависеть от координат электрона, а это означает, что электрон с равной вероятностью может быть в любом месте кристалла. Такой электрон называется свободным или коллективизированным.

Если внешнее поле отсутствует, то средняя скорость свободных электронов равна нулю из-за хаотичности распределения электронов по скоростям. При наличии внешнего поля произойдет перераспределение электронов по состояниям и скоростям, следовательно, средняя скорость электронов станет отличной от нуля, т.е. электроны будут вовлечены в направленное движение.

Такие вещества называются проводниками или металлами.

Для металлов валентная зона является полупустой, т.е. можно считать, что она совпадает с зоной проводимости. Наличие в этой зоне свободных состояний дает возможность внешним электронам легко перераспределяться по состояниям.

По современным представлениям внешние электроны атомов в металле не принадлежат какому-то одному атому, а являются коллективизированными, т.е. принадлежат всему кристаллу, их называют электронным газом.

Поведение электронного газа в сильной степени зависит от соотношения между температурой кристалла и температурой Ферми.

Различают два предельных случая:

1. Если температура кристалла много меньше температуры Ферми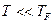, т.е.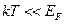, электронный газ называется вырожденным и он подчиняется квантовой статистике Ферми-Дирака..

2. Если же , т.е. 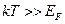, электронный газ называется невырожденным и он подчиняется классической статистике.

Температура Ферми для металлов составляет несколько десятков тысяч кельвин, поэтому даже при температуре близкой к температуре плавления металла электронный газ в металле является вырожденным и подчиняется квантовой статистике.

В полупроводниках концентрация свободных электронов много меньше, чем в металлах, соответственно уровень Ферми мал, поэтому уже при комнатной температуре электронный газ во многих полупроводниках оказывается невырожденным и подчиняется классической статистике.

В узлах кристаллической решетки расположены положительные ионы. Свободные электроны двигаются в пространстве между ионами, создавая взаимодействие, которое не позволяет ионам удалиться друг от друга. Это разновидность гетерополярной связи, которую называют металлической.

Свободный электрон в металле подобен частице в ящике с непроницаемыми стенками. При попадании на границу металлического кристалла плоская волна, описывающая движение свободного электрона, отражается и движется в противоположном направлении. При наложении падающей и отраженной волн образуется стоячая волна.

Решение квантовомеханической задачи о движении электронов в кристалле приводит к выводу, что в случае идеальной кристаллической решетки электроны проводимости не испытывали бы при своем движении никакого сопротивления и электропроводность металла была бы бесконечно большой. Однако этого никогда не бывает. Нарушения строгой периодичности в решетке бывают обусловлены наличием примесей или вакансий (отсутствие атомов в узлах решетки), а также тепловыми колебаниями решетки.

Рассеяние электронов на атомах примеси приводит к возникновению электросопротивления. Чем чище металл и ниже температура, тем меньше электросопротивление.

Удельное электрическое сопротивление металлов можно представить в виде суммы двух слагаемых

,

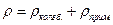где 1-ое слагаемое – это сопротивление, обусловленное тепловыми колебаниями решетки, оно уменьшается с понижением температуры и обращается в нуль при Т=0 К.

2-ое - обусловлено рассеянием электронов на атомах примеси не зависит от температуры и образует остаточное сопротивление металла.

Среднюю скорость свободных электронов в металле называют дрейфовой скоростью:

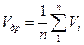, где n- концентрация электронов в металле.

В отсутствии внешнего поля дрейфовая скорость равна нулю и электрический ток в металле отсутствует. При наложении внешнего поля напряженностью E дрейфовая скорость становится отличной от нуля – в металле возникает электрический ток.

Количественной характеристикой электрического тока является вектор плотности тока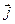

,

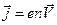где n- концентрация свободных электронов, 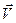- скорость направленного движения носителей тока.

Воздействие кристаллической решетки на движущейся электрон можно определить как некоторую силу сопротивления, препятствующую его движению:

,

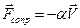где 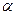- положительный коэффициент.

Со стороны внешнего поля на электрон действует сила:

.

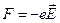Движение электрона в постоянном электрическом поле носит стационарный характер, следовательно:

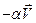
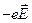= 0

Скорость направленного движения электрона пропорциональна напряженности внешнего поля ,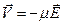

где 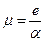называется подвижностью электрона.

В результате получим закон Ома в дифференциальной форме:

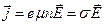
где 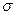- удельная проводимость.

в) сверхпроводимость.

В 1911 году Камерлинг обнаружил, что электрическое сопротивление ртути при Т = 4, 15 К скачкообразно обращается в нуль. Это явление было названо сверхпроводимостью.

Температура, при которой происходит переход в сверхпроводящее состояние, называется критической температурой .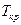

Экспериментально сверхпроводимость можно наблюдать двумя способами:

1. Включить в общую электрическую цепь, по которой течет ток, звено из сверхпроводника, находящегося при температуре ниже критической. В момент перехода в сверхпроводящее состояние разность потенциалов на концах этого звена обращается в ноль.

2. Можно поместить кольцо из сверхпроводника в магнитное поле, направленное перпендикулярно плоскости кольца. Затем, охладив кольцо до температуры ниже 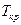, выключить поле. В результате в кольце возникает незатухающий индукционный ток, который циркулирует по кольцу бесконечно долго.

В 1959 году Коллинз не обнаружил уменьшение силы тока в таком кольце, наблюдая за ним в течение 2,5 лет.

Сверхпроводимость представляет собой явление, в котором квантовомеханические эффекты обнаруживаются не в микроскопических, а в макроскопических масштабах.

Теория сверхпроводимости очень сложна, поэтому ограничимся её изложением на уровне научно-популярной литературы.

Разгадка сверхпроводимости заключается в том, что электроны в металле кроме кулоновских сил отталкивания испытывают особый вид взаимного притяжения, которое в сверхпроводящем состоянии преобладает над отталкиванием. В результате электроны объединяются, в так называемы, куперовские пары.

Электроны, входящие в такую пару имеют противоположно направленные спины, поэтому общий спин пары равен нулю. Такая пара представляет собой бозон.

Бозоны склонны накапливаться в основном энергетическом состоянии, из которого их довольно сложно перевести в возбужденное состояние, следовательно, куперовские пары, придя в согласованное движение, остаются в этом состоянии неограниченно долго. Согласованное движение куперовских пар и есть ток сверхпроводимости.

В куперовские пары объединяются не все электроны проводимости. При температуре отличной от абсолютного нуля имеется некотороя вероятность того, что пара будет разрушена. Поэтому всегда наряду с куперовскими парами в кристалле всегда имеются и нормальные электроны, движущиеся по кристаллу обычным способом. Чем ближе температура к критической, тем доля нормальных электронов растет, обращаясь в единицу при 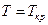. Поэтому при температуре выше критической сверхпроводящее состояние невозможно.

В 1986-1987 годах был обнаружен ряд высокотемпературных сверхпроводников с критической температурой порядка 100К. Все открытые до сих пор сверхпроводники принадлежат к группе металлооксидной керамики.

г) Рассмотрим теперь вещество, у которого энергия Ферми лежит в запрещенной зоне между валентной зоной и зоной проводимости.

Рис. 35.

Если энергия состояния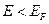,то для всех зон кроме валентной функция Ферми-Дирака будет равна единице. Если энергия состояний 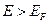, то для всех зон кроме зоны проводимости 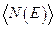будет равна нулю.

Отличными от нуля в 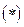будут два слагаемых, и они будут соответствовать валентной зоне и зоне проводимости.

.

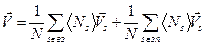Полупроводники отличаются от диэлектриков только шириной запрещенной зоны и тепловое движение в них способно перебросить электрон из валентной зоны в зону проводимости.

Дата добавления: 2014-01-07