Дифференцируемость и непрерывность. Касательная и нормаль к графику функции

Касательная и нормаль к графику функции.

Определение производной. Механический, геометрический, экономический смысл производной.

Лекция 1. Дифференциальное исчисление функции одной переменной.

1.1. Определение производной. Механический, геометрический, экономический смысл производной.

Пусть функция 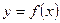определена на множестве 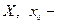внутренняя точка множества X, то есть принадлежит множеству с некоторой своей окрестностью. Аргументу 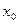дадим приращение 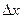, при этом функция получит приращение

Определение. Производной функции в точке 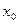называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к 0, то есть

При этом используются обозначения:

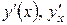– по Лагранжу; 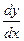– по Лейбницу; – по Ньютону.

Запись 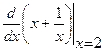следует понимать как производную функции в точке .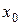

Физический смысл производной заключается в том, что

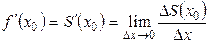– мгновенная скорость прямолинейного движения в момент времени . В самых различных задачах (в том числе и экономических) производная функции интерпретируется как скорость изменения величины y относительно величины x.

Геометрический смысл производной: рассмотрим график функции 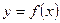, MM₀ – секущая.

Определение. Касательной к графику функции 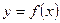в точке M₀ называется предельное положение секущей MM₀, когда точка M движется к точке M₀ по графику функции .

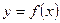Также: 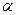– угол наклона касательной к оси оx, 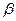– угол наклона секущей к оси оy.

Если .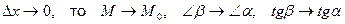

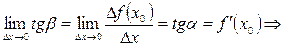
Рассмотрим : ; 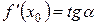– производная функции в точке 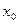есть тангенс угла наклона касательной к графику функции 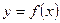в точке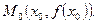

Замечание. 1) Если существует конечная производная 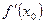, то к графику функции 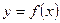в точке 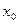можно провести единственную касательную;

2) Если , то касательная к графику функции 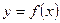в точке 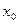параллельна оси оx.

3) В точке 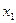касательная не существует и производная функции также не существует.

Дата добавления: 2014-01-07