Теорема Ролля

Теорема.

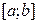Пусть функция непрерывна на , дифференцируема на и на концах отрезка в точках a и b принимает одинаковые значения , тогда 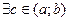, в которой .

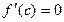Доказательство. Если , то 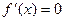, то есть в качестве точки c можно взять любую точку, принадлежащую .

Если не тождественна константе, то с учетом условия о непрерывности на 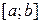по теореме Вейерштрасса можно утверждать, что принимает на этом отрезке наибольшее и наименьшее значения в точках 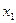и , у которых хотя бы одна попадёт внутрь . Пусть , . Так как функция дифференцируема на 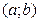, то она дифференцируема в точке 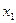и по теореме Ферма , то есть в качестве точки c можно взять точку .

Геометрический смысл теоремы Ролля.

На найдется хотя бы одна точка, в которой касательная параллельна оси 0X.

Алгебраический смысл теоремы Ролля.

Между двумя последовательными корнями дифференцируемой функции

лежит хотя бы один корень её производной.

Замечание.

Все три требования теоремы Ролля существенны. При нарушении

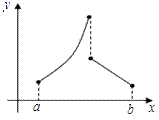хотя бы одного из них заключение теоремы может оказаться неверным.

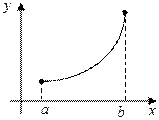
Дата добавления: 2014-01-07