Методы нормирования погрешностей средств измерений

Для того, чтобы ориентироваться в метрологических свойствах конкретного средства измерения, чтобы заранее оценить погрешность, которую внесёт данное СрИз в результате измерения, пользуются нормированными значениями погрешности, под которыми понимают погрешность, являющуюся предельной для данного типа СрИз. При этом погрешности отдельных экземпляров СрИз одного и того же типа могут различаться, но не должны превышать указанные для них нормы. Таким образом, нормируется основная и дополнительные погрешности, которые заносятся в паспорт каждого экземпляра средств измерений.

Основной метрологической характеристикой средства измерения является класс точности, который определяет гарантированные значения основной и дополнительных погрешностей, а также другие свойства СрИз, влияющие на точность. Основные способы установления пределов допускаемых погрешностей и обозначения классов точности СрИз установлены ГОСТ.8.401-80 “ГСИ. Классы точности средств измерений”. Основная погрешность СрИз нормируется четырьмя различными способами, что обусловлено разным соотношением аддитивной и мультипликативной составляющих в общей погрешности СрИз.

1. При чисто мультипликативной полосе погрешностей СрИз абсолютная погрешность D_м возрастает прямо пропорционально текущему значению измеряемой величены Х. Поэтому относительная мультипликативная погрешность или погрешность чувствительности такого СрИз d_s=D_м/C оказывается величиной постоянной при любом значении Х и используется для нормирования погрешностей такого СрИз и указания класса точности: класс точности при этом указывается в виде значения d_s, выраженного в процентах. Абсолютная погрешность определяется по формуле 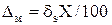. Для этого случая, кроме значения d_s, указываются границы рабочего диапазона измеряемой величины, в пределах которых такая оценка оказывается справедливой.

2. При чисто аддитивной полосе погрешностей остаётся неизменной при любых значениях Х граница абсолютной погрешности нуля D₀. Так как нормировать абсолютные значения погрешности неудобно, то нормируют приведённое значение этой погрешности g₀=D₀/C_N, где C_N - нормирующее значение. Значение приведённой погрешности g₀, выраженное в процентах, используется для обозначения класса точности таких средств измерений. Текущее значение относительной погрешности d=D₀/C растёт обратно пропорционально Х (рис.1.17) и при Х=D₀ d=100%.

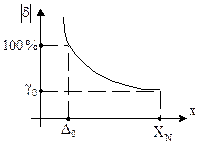
Рис.1.17

Такое значение измеряемой величины, когда Х=D₀ и d=100%, называется порогом чувствительности средства измерения.

3.При одновременном присутствии аддитивной и мультипликативной составляющих текущее значение абсолютной погрешности определяется двучленной формулой

D(C)=D₀+d_sC,

где D₀- аддитивная, а d_sC- мультипликативная составляющие абсолютной погрешности (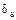в этом случае указывается в относительных единицах).

Разделив все члены этого уравнения на предел измерения Х_к, получим приведённую погрешность g_пр для этого случая

,

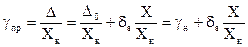где g_н=D₀/Х_к называется приведённой аддитивной погрешностью в начале диапазона. Относительное значение погрешности при этом будет равно

.

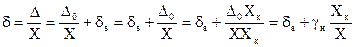Отсюда следует, что при Х=Х_к эта погрешность будет равна d(Х_к)=g_к=d_s+g_н. Класс точности таких приборов указывается двумя числами, записываемыми через косую черту g_к/g_н, где g_к- приведённая погрешность (в процентах) в конце диапазона, а g_н- приведённая погрешность в начале диапазона.

4. ГОСТ 8.401-80 разрешает использовать специальные формулы нормирования погрешностей. Например, в измерительных приборах с очень широким диапазоном измерения полоса погрешностей выражается трехчленной формулой

,

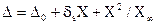где C_¥- постоянное значение, присущее данному измерительному прибору, при котором погрешность достигает 100% из-за потери чувствительности к изменению больших значений измеряемой величены. Предельное значение относительной погрешности будет равно

.

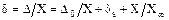Согласно ГОСТ 8.401-80 для указания нормированных значений погрешностей d_s,g_н,g_к не могут использоваться произвольные цифры. Выражение в процентах они могут иметь значения 6-4-2.5-1.5-1.0-0.5-0.2-0.1-0.05-0.02-0.01-0.005-0.002-0.001 и т.д. Если же для указания погрешности используются специальные формулы, то могут использоваться и другие числа.

Значение класса точности прибора маркируется на его шкале. При этом используются следующие условные обозначения.

Если класс точности (КТ) прибора установлен по значению погрешности чувствительности d_s (погрешность чисто мультипликативная), то обозначаемое на шкале значение класса точности обводится кружком.

Например, в кружке обозначает, что d_s=±1.5%.

Если полоса погрешностей принята аддитивной и прибор нормируется по приведённой аддитивной погрешности g₀(таких приборов большинство), то класс точности указывается без каких-либо подчеркиваний. Например,1.5 обозначает, что g₀=±1.5%.

Обозначение класса точности в виде дроби 0.02/0.01 указывает, что погрешность прибора нормирована по двухчленной формуле с g_н=±0.01% и g_к=±0.02%.

Для трехчленной формулы погрешности в паспорте этого прибора указывают нормированные значения D₀,d_s и C_¥.

Таким образом, обозначение КТ прибора даёт достаточно полную информацию для вычисления предельной оценки погрешности результатов измерения.

При нормировании погрешностей сложных СрИз двухчленной формулой ГОСТ 8.401-80 предусматривает несколько иное её написание через значения g_н и g_к. Так как g_s=g_к-g_н, то

.

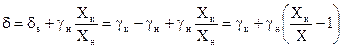В технической литературе часто g_к обозначают через с, а g_н- через d. Тогда эта формула приобретает вид

;

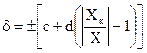например, 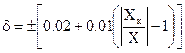означает, что класс точности этого Ср.Из. 0.02/0.01.

Результат измерения имеет ценность лишь тогда, когда можно оценить его интервал неопределённости, т.е. степень достоверности. Поэтому согласно ГОСТ 8.011-72 ”Показатели точности измерений и формы представления результатов измерения” сообщение о любом результате измерений должно сопровождаться указанием его погрешности. Вычисляться должна как абсолютная, так и относительная погрешность результата измерения, так как первая из них нужная для округления результата и его правильной записи, а вторая – для однозначной сравнительной характеристики его точности.

Для разных способов нормирования погрешностей СрИз эти вычисления производятся по разному, поэтому рассмотрим три характерных случая.

1. Класс точности указан в виде числа d_s, заключённого в кружок. Тогда относительная погрешность результата в процентах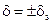, а абсолютная погрешность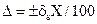

2. Класс точности указан одним числом 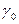(без кружка). Тогда абсолютная погрешность результата измерения 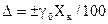, где 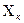- предел измерения, на котором он производится, а относительная погрешность 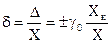. В этом случае должен быть зафиксирован и предел измерения 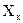, иначе в последствии нельзя будет вычислять погрешность результата.

3. Класс точности прибора указан двумя числами в виде 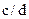(). В этом случае удобно сначала вычислять относительную погрешность d, а затем найти абсолютную как.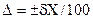

В ряде случаев для приборов, у которых значение погрешности указывается двухчленной формулой, требуется определить раздельно значения аддитивной и мультипликативной составляющих.

Преобразуя формулу для относительной погрешности, можно получить:

аддитивная составляющая абсолютной погрешности ;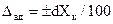

мультипликативная составляющая абсолютной погрешности ;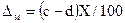

аддитивная составляющая относительной погрешности ;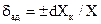

мультипликативная составляющая относительной погрешности .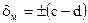

Рассчитывая значения погрешности, особенно при использовании электронного калькулятора, значения погрешностей получают с большим числом знаков. Однако исходными данными для расчета являются нормированные значения погрешности СрИз, которые указываются с одной или двумя значащими цифрами.

Вследствие этого в окончательном значении рассчитанной погрешности должны быть оставлена только первые одна-две цифры.

Существует три правила округления рассчитанного значения погрешности и полученного экспериментального результата измерения.

Погрешность результата измерения указывается двумя значащими цифрами, если первая из них 1или 2, и одной, если первая есть 3 и более.

Результат измерения округляют до того же десятичного разряда, которым оканчивается округлённое значение абсолютной погрешности.

Округление производится лишь в окончательном ответе, а все предварительные вычисления производятся с одним-двумя лишними знаками.

Например: 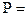38,64 Вт, D=±1.24 Вт

Результат 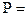(38.6±1.2) Вт, 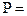0.95

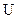=123.6мВ, D=±6.17мВ

Результат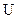=(124±6)мВ, 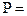0.9

Дата добавления: 2014-01-07