
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Внутренние силы и моменты
|
|
|
|
Внутренними силами (моментами) для машины являются силы (моменты) взаимодействия между деталями ее механизмов. Это отличает внутренние силы от внешних сил взаимодействия между внешней средой и машиной.
Из внутренних сил основное влияние на условия движения машины оказывают момент двигателя и силы (моменты) сопротивления в агрегатах машины: силовой установке, силовой передаче и ходовой части.
Наличие внутренних сопротивлений обусловливает потери энергии в механизмах, из-за которых уменьшается энергия, используемая для преодоления внешних сопротивлений.
Иногда в подвеске расходуется до 20 – 30 % от общего расхода энергии при движении.
Потери мощности в силовой установке.
Движение автомобиля обусловлено подводом крутящего момента двигателя к его колесам через агрегаты трансмиссии.
В настоящее время на колесных машинах в основном применяются двигатели внутреннего сгорания, дизельные или карбюраторные (бензиновые). Мощность этих двигателей принято оценивать скоростными характеристиками, представляющими зависимость эффективной мощности или крутящего момента на коленчатом валу при установившемся режиме работы от частоты вращения коленчатого вала двигателя. Скоростная характеристика, полученная при полной подаче топлива, называется внешней скоростной характеристикой.
Внешние, скоростные характеристики определяются на специальных тормозных стендах. Поскольку внешняя характеристика определяет предельные режимы работы двигателя, именно она является наиболее существенной при оценке тягово-скоростных свойств автомобиля. Как правило, скоростные характеристики приводятся в различной справочной и технической литературе.
Общий вид внешней, скоростной характеристики представлен на рис.2.9.
 Рис.2.9.
Рис.2.9.
В случае отсутствия последней, зависимость крутящего момента или мощности двигателя при полной подаче топлива от частоты вращения коленчатого вала можно определить по эмпирической формуле (С. Л. Лейдермана).

где  - текущее значение мощности двигателя, кВт;
- текущее значение мощности двигателя, кВт;
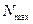 - максимальная мощность двигателя, кВт;
- максимальная мощность двигателя, кВт;
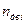 - текущая частота вращения коленчатого вала двигателя, мин-1;
- текущая частота вращения коленчатого вала двигателя, мин-1;
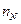 - частота вращения коленчатого вала двигателя при N max, мин-1;
- частота вращения коленчатого вала двигателя при N max, мин-1;
 - опытные коэффициенты.
- опытные коэффициенты.
Для карбюраторных двигателей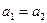
 , для двухтактных дизелей
, для двухтактных дизелей  0,87,
0,87, 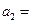 1,13,
1,13, 
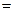 1,0;
1,0; для четырехтактных двигателей
для четырехтактных двигателей  0,53,
0,53, 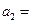 1,56,
1,56, 
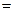 1,09
1,09
При использовании в расчетах формулы С. Л. Лейдермана берется частота вращения коленчатого вала двигателя, а, задаваясь промежуточными текущими значениями его частоты вращения, получают мощность двигателя.
Когда характеристика двигателя снимается на стенде, то часть оборудования и приборов (воздухоочиститель, насос рулевого усилителя и др.) на него не устанавливаются. Поэтому условия работы двигателя, установленного на автомобиле, отличаются от стендовых, т.е. он работает с другими впускными и выпускными системами, устанавливается все необходимое оборудование, приборы и механизмы, на привод которых затрачивается энергия (мощность). Поэтому мощность установленного двигателя будет меньше. Если вентилятор системы охлаждения работает на стенде, то потребляемая им мощность значительно меньше, чем в действительных условиях на автомобиле. Это объясняется большим сопротивлением реальных воздушных траков (особенно на специальных машинах). Кроме этого, двигатель работает в другом температурном режиме. При использовании для тягово-скоростных расчетов значения мощностей, полученных из внешних характеристик, уменьшаются путем умножения на коэффициент потерь (Кс), зависящий от типа двигателя и автотранспортного средства. В приближенных расчетах можно принимать Кс = 0,85 – 0,9, т.е. потери на привод различных механизмов и узлов, устанавливаемых на автомобиль, и получающих привод от двигателя составляют 10 – 15%.
Для более точных расчетов можно пользоваться следующими данными, характеризующими потери мощности в процентах на привод различных механизмов и узлов:
масляный насос - 1,0 – 1,5;
водяной насос - 2,0 – 4,0;
вентилятор - 4,0 – 8,0;
генератор - 0,3 – 0,4;
воздушный фильтр - 1,0 – 1,5;
компрессор - 3,0 – 6,0;
насос рулевого усилителя - 2,0 – 4,0.
Необходимо иметь в виду, что большие значения относятся к двигателям с меньшей мощностью.
Учитывая все вышесказанное можно сделать вывод, что мощность, расходуемая двигателем на совершение полезной работы (без учета потерь в агрегатах трансмиссии и ходовой части) составит:

Потери мощности в агрегатах трансмиссии. КПД трансмиссии.
Наибольшие потери мощности имеют место в коробках передач, раздаточных коробках, главных передачах и колесных редукторах. Потери мощности в отдельных механизмах трансмиссии в целом могут быть найдены экспериментально на специальных испытательных стендах или путем испытаний автомобилей.
Исследованиями установлены некоторые общие закономерности изменения КПД трансмиссий в зависимости от типа агрегата и режима его работы.
Экспериментальными исследованиями показано, что потери мощности в трансмиссии можно представить двумя составляющими: потерями. Обусловленными наличием трения в узлах, передающих нагрузку (трение в зацеплении шестерен, в карданных сочленениях, в подшипниках) и потерями, вызванными разбрызгиванием масла в картерах (гидравлические потери), причем к этой же группе можно отнести потери мощности на трение в сальниках.
Первая группа потерь характерна тем, что при увеличении передаваемого через трансмиссию крутящего момента потери на трение возрастают медленнее, чем возрастает передаваемый трансмиссией крутящий момент. Вследствие чего несколько увеличивается КПД механизмов.
Гидравлические потери практически не зависят от передаваемого момента, а определяется только частотой вращения валов, шестерен, вязкостью и объемом масла в картерах. При увеличении частоты потери мощности на перемешивание и разбрызгивание масла в картерах возрастает более интенсивно, чем передаваемая мощность и КПД редукторного механизма уменьшается. КПД возрастает при уменьшении вязкости масла, уменьшении его уровня (объема) и повышении его температуры. Поэтому за уровнем масла в процессе эксплуатации необходимо постоянно следить.
С точки зрения уменьшения потерь мощности целесообразно иметь агрегаты с сухим картером и принудительной подачей масла к трущимся поверхностям.
Большое значение на потери мощности оказывает тип зацепления шестерен и количество полюсов зацепления, как силовых (нагруженны) так и холостых.
Для расчетов можно использовать экспериментально установленные значения КПД шестеренчатых зацеплений. Считается, что пара цилиндрических шестерен пе5редает крутящий момент (мощность) с КПД:
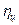 = 0,98 и конических
= 0,98 и конических 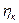 = 0,87.
= 0,87.
Гидравлические потери можно определить, замеряя момент необходимый для прокручивания незагруженного редуктора. А гидравлические потери во всей трансмиссии обычно определяют экспериментально совместно с потерями в подшипниках ведущих колес, прокручивая трансмиссию с заданной скоростью при вывешанных колесах. Если известен момент (Мх), потребный для прокручивания незагруженной трансмиссии, ее КПД можно найти по формуле.
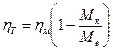 (3)
(3)
где 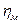 - КПД шестеренчатых зацеплений, через которые передается момент двигателя при полной подаче топлива, необходимый для движения автомобиля в заданных условиях.
- КПД шестеренчатых зацеплений, через которые передается момент двигателя при полной подаче топлива, необходимый для движения автомобиля в заданных условиях.
КПД редукторных механизмов зависит от режимов работы. Например, на низших передачах в коробке передач крутящий момент передается, как правило, через две пары шестерен, ее КПД будет ниже, чем на прямой передаче.
В главной передаче, при движении на низших передачах, передается большой крутящий момент, а частота вращения валов малая, поэтому ее КПД будет выше, чем при движении на больших скоростях. Поэтому, при расчетах можно считать, что общий КПД трансмиссии не зависит от режима ее работы.
Для расчетов рекомендуется следующие значения КПД отдельных механизмов:
коробки передач 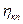 = 0,96 – 0,98
= 0,96 – 0,98
раздаточные коробки  = 0,93 – 0,97
= 0,93 – 0,97
колесного редуктора  = 0,96 – 0,98
= 0,96 – 0,98
карданного шарнира  = 0,995 (но при углах более 8 – 100 КПД резко снижается).
= 0,995 (но при углах более 8 – 100 КПД резко снижается).
главной передачи  = 0,93 – 0,97
= 0,93 – 0,97
Общий КПД трансмиссии равен произведению КПД агрегатов, через которые последовательно проходит мощность (передается крутящий момент).

При работе двигателя по внешней скоростной характеристике КПД механической трансмиссии можно считать равным ηТ = 0,8 – 0,92 (меньшие значения относятся к полно приводным автомобилям, а большие к легковым).
УРАВНЕНИЯ ДИНАМИКИ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ АВТОМОБИЛЯ.
При движении автомобиля следует учитывать большое количество факторов, влияющих на положение автомобиля в пространстве. От них зависит взаимодействие автомобиля с дорогой и его возможности по совершению транспортной работы.
Закономерности динамики автомобиля описываются уравнениями динамики прямолинейного движения.
Уравнения динамики прямолинейного движения автомобиля устанавливают зависимость между внешними и внутренними силами и позволяют определять величины неизвестных сил, когда задано необходимое число известных.
Таких уравнений два: уравнение равновесия и уравнение мощностей.
1. Первое уравнение динамики – уравнение сил (уравнение равновесия).
Рассмотрим наиболее общий случай движения автомобиля – движение на подъем с ускорением (рис.2. 10).
Для составления уравнения спроектируем на ось Х – Х все внешние силы, действующие на автомобиль.
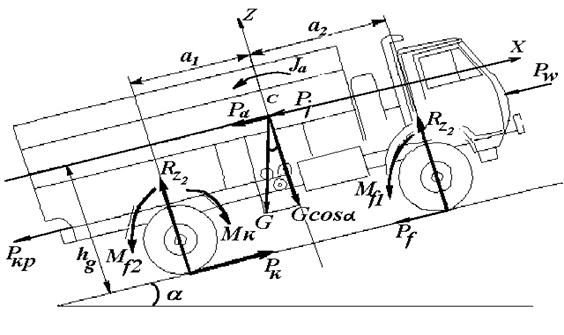
Рис.2.10
Сгруппировав движущие силы сопротивления, получим:
 ,
,
где 

Полученное уравнение является первым уравнением динамики в общем, виде.
Подставим в уравнение значение входящих в него сил. Силу сопротивления воздуха на прицеп учитываем увеличенным значением коэффициента сопротивления воздуха

После простейших преобразований:
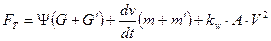
Полученное выражение является уравнением динамики в развернутом виде.
Если автомобиль одиночный, т.е. 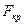 = 0, тогда
= 0, тогда
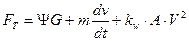
Первое уравнение динамики показывает, какая сила тяги на ведущих колесах должна развиваться, чтобы преодолеть внешние силы сопротивления движению.
В первом уравнении динамики имеется два неизвестных:
сила тяги на ведущих колесах «FТ» и ускорение «( )".
)".
Для решения уравнения необходимо составить второе уравнение, которым и будет второе уравнение динамики или уравнение мощностей.
2.Второе уравнение динамики – уравнение мощностей.
Вывод второго уравнения динамики основан на теореме о кинетической энергии: изменение мощности движущегося тела равно мощности, затраченной на преодоление сил сопротивления, действующих на пути движения.
Таким образом, в случае ускоренного движения можно записать:

где  - мощность двигателя за вычетом потерь на привод вспомогательных агрегатов;
- мощность двигателя за вычетом потерь на привод вспомогательных агрегатов;
 - мощность, затрачиваемая на ускорение вращения деталей двигателя, коленчатого вала, маховика с кожухом сцепления и т.д.;
- мощность, затрачиваемая на ускорение вращения деталей двигателя, коленчатого вала, маховика с кожухом сцепления и т.д.;
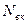 - мощность на ведущих колесах, расходуемая на преодоление внешних сопротивлений;
- мощность на ведущих колесах, расходуемая на преодоление внешних сопротивлений;
 - мощность, затрачиваемая на ускорение вращения колес автомобиля и непосредственно связанных с ними деталей (полуосей, полуосевых шестерен);
- мощность, затрачиваемая на ускорение вращения колес автомобиля и непосредственно связанных с ними деталей (полуосей, полуосевых шестерен);
 - мощность, затрачиваемая на ускорение вращения колес прицепа.
- мощность, затрачиваемая на ускорение вращения колес прицепа.
Выразим значения мощности, затрачиваемой на преодоление внешних сопротивлений NВК через первое уравнение динамики, а мощностей, затрачиваемых на раскрутку вращающихся деталей автомобиля и прицепа через моменты их инерции.
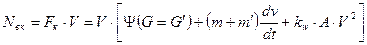


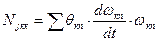
где 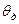 - момент инерции вращающихся деталей двигателя, приведенной к маховику;
- момент инерции вращающихся деталей двигателя, приведенной к маховику;
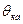 - момент инерции колес автомобиля;
- момент инерции колес автомобиля;
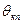 - момент инерции колес прицепа;
- момент инерции колес прицепа;
 - угловые скорости соответственно двигателя, колес автомобиля и колес прицепа.
- угловые скорости соответственно двигателя, колес автомобиля и колес прицепа.
Выразив значения угловых скоростей через скорость движения автомобиля ( ) и подставим эти значения в вышеназванные выражения получим:
) и подставим эти значения в вышеназванные выражения получим:

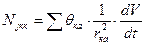

где 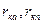 - радиусы колеса соответственно автомобиля и прицепа;
- радиусы колеса соответственно автомобиля и прицепа;
 - передаточное число трансмиссии;
- передаточное число трансмиссии;
 - к.п.д. трансмиссии.
- к.п.д. трансмиссии.
Подставим значения в вышеназванные выражения, и после преобразования получим:
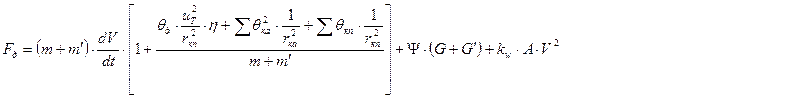
где 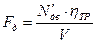 - сила тяги по двигателю
- сила тяги по двигателю
Указанное уравнение называют вторым уравнением динамики (уравнением мощн6ости) в развернутом виде:
Выражение, взятое в скобках, в уравнении часто для сокращения записи заменяют символом «δ» и называют коэффициентом учета вращающихся масс, т.е.


Тогда уравнение мощности примет вид:

Это уравнение в литературе принято называть уравнением тягового баланса, которое показывает расход мощности двигателя на движение автопоезда с дополнительными затратами на разгон автопоезда.
ЛЕКЦИЯ 5
Смысл безразмерного коэффициента учета вращающихся масс состоит в том, что он позволяет все слагаемые, имеющие размерность массы (показывающие меру инерционности) заменить одним слагаемым – массой машины, увеличенной в « » раз.
» раз.
Физический смысл коэффициента учета вращающихся масс состоит в том, что в динамике (с учетом разгона или торможения) автомобиля инерционные составляющие зависят не просто от наличия тех или иных масс. Разгон или замедление, которых приводит к появлению дополнительных сил, а от наличия в составе автомобиля массивных быстровращающихся элементов, которые обладают способностью накапливать кинетическую энергию при разгоне, и отдавать ее при замедлении автомобиля.
Эти быстровращающиеся элементы автомобиля напоминают инерционный двигатель, представляющий собой массивный маховик, запасающий кинетическую энергию на стоянке при его раскрутке и отдающий энергию движущемуся транспортному средству.
Конечно, роль вращающихся масс на реальных автомобилях не столь значительна, как в случае использования инерционного двигателя, но в ряде случаев учет их совершенно необходим.
Так, в случае движения одиночного автомобиля доля энергии, идущая на разгон вращающихся масс относительно больше, чем в случае движения автопоезда.
Для одиночного автомобиля уравнение тягового баланса имеет вид:
 ,
,
где 
Из приведенной формулы видно, что величина коэффициента « » зависит от большого числа параметров, но наиболее существенный вклад обеспечивает величина общего передаточного отношения трансмиссии «
» зависит от большого числа параметров, но наиболее существенный вклад обеспечивает величина общего передаточного отношения трансмиссии «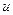 mр».
mр».
Расчет показывает, что при движении на высшей передаче величина « » составляет 1,04 – 1,09 а при переходе на низшие передачи эта величина в некоторых случаях достигает 4 – х единиц.
» составляет 1,04 – 1,09 а при переходе на низшие передачи эта величина в некоторых случаях достигает 4 – х единиц.
Это означает, что при разгонах на высших передачах доля энергии, затрачиваемой на раскрутку вращающихся деталей автомобиля относительно невелика по сравнению с долей энергии, расходуемой на увеличение скорости движения всего автомобиля.
На низших передачах, поскольку кинетическая энергия самого автомобиля сравнительно мала, а затраты на разгон вращающихся деталей практически такие же как и на высших передачах, отношение затрат мощности резко изменяется в связи с чем величина коэффициента возрастает.
Если величины моментов инерции двигателя и колес неизвестны, то для ориентировочных расчетов, а также для контроля правильности определения порядка величины « » можно пользоваться эмпирической формулой:
» можно пользоваться эмпирической формулой:



где 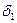 - коэффициент, учитывающий вращающиеся массы колес принимают
- коэффициент, учитывающий вращающиеся массы колес принимают 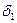 = 0,03 + 0,05
= 0,03 + 0,05
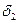 - коэффициент, учитывающий вращающиеся массы элементов трансмиссии двигателя:
- коэффициент, учитывающий вращающиеся массы элементов трансмиссии двигателя: 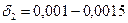
 - передаточное число трансмиссии.
- передаточное число трансмиссии.
Иногда требуется определить коэффициент учета вращающихся масс при движении накатом. В этом случае в формуле расчета « » часть параметров принимают равной нулю (
» часть параметров принимают равной нулю (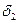 ,
,  ). Тогда на величину коэффициента влияют только параметры колес. В этом случае коэффициент учета вращающихся масс принимают равным - 1,05
). Тогда на величину коэффициента влияют только параметры колес. В этом случае коэффициент учета вращающихся масс принимают равным - 1,05
Такого же порядка берется коэффициент для расчета инерционной силы для прицепа.
При равномерном движении изменение скорости равно нулю, а значит, инерционная сила также равна нулю.

 при
при 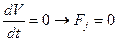
Тогда сила тяги по двигателю равна окружной силе на ведущих колесах
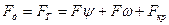
В случае замедленного движения автомобиля, вращающиеся массы двигателя и трансмиссии вследствие своей инерционности стараются поддержать высокую скорость движения, что необходимо учитывать при торможении автомобиля, преодолении препятствий с разгона и т.п.
При разгоне с точки зрения экономичности желательно переходить на высшие передачи, как только позволяют дорожные условия, т.к. доля энергии, затрачиваемая непосредственно на ускорение движения автомобиля на высших передачах выше.
В случае использования на автомобиле непрерывной (но ступенчатой передачи. Например, гидромеханической, величина коэффициента учета масс может находиться несколько иначе, т.к. для непрерывной передачи происходит изменение передаточного отношения в ходе изменения скорости автомобиля.


где 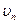 - постоянное передаточное отношение в планетарной или вальной коробке передач, соединенной с гидротрансформатором;
- постоянное передаточное отношение в планетарной или вальной коробке передач, соединенной с гидротрансформатором;
 - передаточное отношение гидротрансформатора;
- передаточное отношение гидротрансформатора;
 - угловая скорость ведущего вала гидротрансформатора;
- угловая скорость ведущего вала гидротрансформатора;
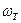 - угловая скорость ведомого вала гидротрансформатора.
- угловая скорость ведомого вала гидротрансформатора.
Производная  характеризует зависимость изменения угловой скорости ведущего вала гидротрансформатора от изменения угловой скорости ведомого вала (т.е. «прозрачность»).
характеризует зависимость изменения угловой скорости ведущего вала гидротрансформатора от изменения угловой скорости ведомого вала (т.е. «прозрачность»).
ДИНАМИЧЕСКАЯ ХАРАКТЕРИСТИКА АВТОМОБИЛЯ.
Режимы движения машины. Тягово–скоростные свойства машины. Тяговые расчеты машин. Поверочный тяговый расчет машины с механической ступенчатой трансмиссией. Тяговая и динамические характеристики машины
Одним из основных путей повышения эффективности использования автомобильной транспортной техники (АТС) является повышение технического уровня конструкции автомобилей и, прежде всего, повышение их тягово – скоростных свойств.
Тягово – скоростные свойства являются одним из наиболее важных эксплуатационных свойств колесных машин, определяющих их целевое назначение, поэтому данная тема в курсе «Теория, конструкция и расчет колесных машин» занимает особое место.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1728; Нарушение авторских прав?; Мы поможем в написании вашей работы!