Стандартная форма характеристического полинома, настроенная на минимум квадратичной интегральной оценки

Квадратичная интегральная оценка предусматривает настройку системы по пере5ходному процессу в целом по следующему принципу:

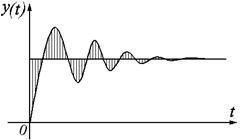
Рис. 2.27.

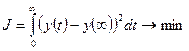(64)

Исходя из этих правил, характеристические уравнения для 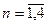имеют вид:

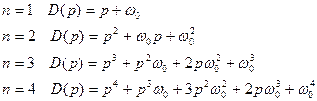(65)

Корни характеристического полинома, настроенные на минимум квадратичной интегральной ошибки, тоже в общем случае являются комплексными корнями с отрицательными действительными частями.

Переходные процессы, соответствующие данным характеристическим уравнениям представлены на рисунке:

Рис. 2.28.

Такие системы, несмотря на минимум в целом квадратичной ошибки, являются более грубыми (σ%≈ 16%)

Пример:

Построить модальный регулятор для объекта (двигатель постоянного тока), обеспечивающим следующие показатели качества: σ %=0%, t_пп=3с.:

Рис. 2.29.

Параметры системы: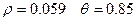

Схема переменных состояния

Рис. 2.30.

Описание в пространстве состояния:

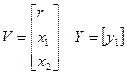
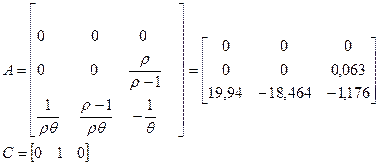
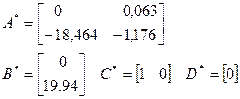
Проверка системы на управляемость:

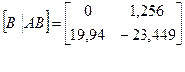
система управляема

Проверка системы на наблюдаемость:

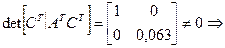система наблюдаема

Наблюдаемость и управляемость являются необходимыми условиями для синтеза.

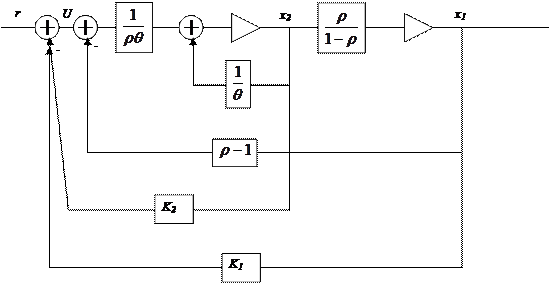
Схема переменных состояния с модальным регулятором

-

Рис. 2.31.

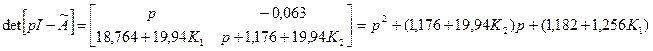Выбираем желаемый характеристический полином в стандартной биномиальной форме, что обеспечивает σ%=0%

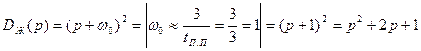
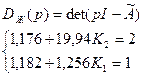
Результаты моделирования САУ с модальным регулятором:

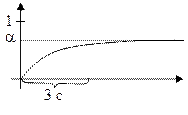
Рис. 2.32.

Дата добавления: 2014-01-07