Приближенное вычисление интеграла Римана

К сожалению, не для любой непрерывной функции можно найти первообразную в виде суперпозиции элементарных функций. Поэтому можно столкнуться с определенным интегралом, для которого применение формулы Ньютона-Лейбница невозможно. Например, .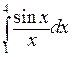

Для таких интегралов приходится применять приближенное интегрирование. Формул приближенного интегрирования довольно много, но все они основаны на ассоциации интеграла с площадью криволинейной трапеции, построенной на основании, совпадающем с отрезком интегрирования. Этот отрезок разбивается на равных частей (для удобства машинного счета) и соответствующие узкие криволинейные трапеции заменяются близкими фигурами, площадь которых легко вычисляется. С ростом площади узких криволинейных трапеций и простейших фигур практически не отличаются друг от друга, поэтому погрешность вычислений можно сделать сколь угодной малой. Мы рассмотрим две простейшие формулы – случаи, когда криволинейные трапеции заменяются прямоугольниками и трапециями.

1. Формула прямоугольников. Для вычисления интеграла 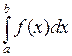отрезок разбивается на равных частей узлами 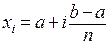. Криволинейная трапеция с основанием заменяется прямоугольником с высотой –либо , либо . Суммируя площади этих прямоугольников с одинаковыми основаниями длины 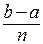, получим либо 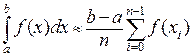, либо .

2. Формула трапеций. Отрезок снова разбивается на равных частей узлами 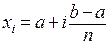. Криволинейная трапеция с основанием заменяется обычной трапецией, причем участок кривой над отрезком заменяется хордой, соединяющей соответствующие точки. Высота такой трапеции равна 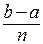, средняя линия равна 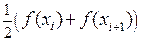. Поэтому, суммируя площади соответствующих трапеций, получим

.

Сосчитаем приведенный выше интеграл 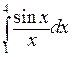двумя способами по формулам прямоугольников с помощью пакета программ MAXIMA. Выберем шаг, равный 3/200.

quad.wxm

Дата добавления: 2014-01-07