
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Местоположение критической точки
|
|
|
|
| Форма пуансона | Положение критической точки b на глубине | Численные значения τ0mаx |
| Круглый плоский с радиусом а Цилиндр с шириной полоски контакта 2а Длинная полоска шириной 2а | 0,637 а 0,78 а а | 0,33Р (Р – среднее) 2Р/πа Р/π (Р – равномерно распределенное давление) |
Следует отметить, что в случае наличия сил трения по поверхности штампа о породу при его перемещении критическая точка b смещается в направлении перемещения пуансона.
Задача Буссинеска позволяет рассчитать нормальные и касательные напряжения в упругом полупространстве под действием статической нагрузки. Однако если пуансон находится в состоянии движения и испытывает трение с окружающей средой, то использование расчетных формул, приведенных выше, оказывается неприемлемым. При поступательном движении пуансона (резца) схема распределения напряжений под действием вертикальной нагрузки существенно иная, чем это следует из задачи Буссинеска. В связи с относительно малыми геометрическими размерами резцов буровых коронок удельное давление на породу под ними можно принять постоянным P(r) = const.
Общая схема разрушения горной породы твердосплавным инструментом предусматривает первоначальное внедрение резца в породу. Дальнейшее поступательное движение резца напоминает процесс резания, когда горная порода разрушается и выдавливается из образовавшейся лунки в виде разрушенных обломков в хрупких и упруго-хрупких породах или в виде стружки в пластичных породах (рис. 16).
Глубина внедрения резца в породу h определяется прочностью породы и осевой силой Р, которая воздействует на резец. Различают три режима разрушения горной породы при вращательном бурении: поверхностное, усталостное, объемное.
Максимальная глубина внедрения пуансона достигается при объемном режиме разрушения горной породы (рис. 17).
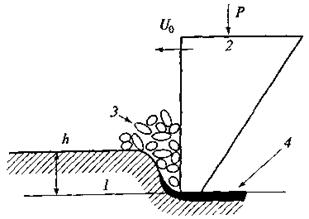
Рис. 16. Схема движения резца под действием силы Р со скоростью U0
1 – горная порода, 2 – резец, 3 – разрушенная порода, 4 – зона уплотнения породы
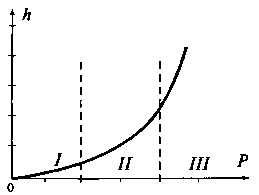
Рис. 17. Зависимость глубины внедрения пуансона в породу от осевой нагрузки:
I, II, III – зоны поверхностного, усталостного, объемного разрушений соответственно

Рис. 18. График зависимости глубины вдавливания клина в горную породу от нагрузки
На рис. 18 показан график зависимости глубины погружения от нагрузки Р при вдавливании клина с углом при вершине 60° в хрупкую горную породу. В начальный период происходит пластическое деформирование, и на этом участке глубина погружения пропорциональна нагрузке до величины h0. Затем глубина погружения скачкообразно возрастает вследствие хрупкого разрушения до величины h1, причем погружение на эту глубину происходит при нагрузке Р, незначительно превышающей нагрузку, соответствующую глубине погружения. При дальнейшем вдавливании вследствие упругой и пластической деформаций глубина погружения растет очень медленно вплоть до нового скачка погружения и т.д.
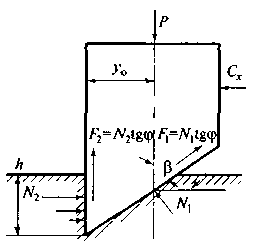
Рис. 19. Схема работы единичного резца твердосплавной коронки
Таким образом, процесс разрушения горных пород при вдавливании заостренных наконечников носит скачкообразный характер.
Рассмотрим работу единичного резца твердосплавной коронки (рис. 19). Под действием осевой нагрузки Р резец внедряется в породу, на лопасть резца действуют реакции породы N1 и N2. Перемещение резца происходит по винтовой линии с углом γ к горизонтали:
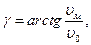 (72)
(72)
где υм – механическая скорость бурения; υ0 – окружная скорость резца на периферии породоразрушающего инструмента.
Имеется в виду, что υ0» υм значения угла γ достаточно малы. Реакции N1 и N2 направлены нормально к передней и задней граням резца. При перемещении резца по граням возникают силы трения N1 tgφ и N2 tgφ, где φ – угол трения резца о породу.
Схема действующих сил находится в равновесии, спроектируем силы на вертикальную и горизонтальную оси:
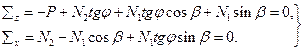 (73)
(73)
Из второго уравнения (73) найдем величину N2:
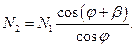 (74)
(74)
Преобразуем (73):
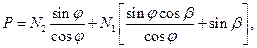 (75)
(75)
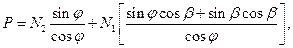 (76)
(76)
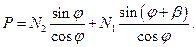 (77)
(77)
Подставим в выражение (77) значение N2 из формулы (74):
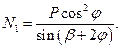 (78)
(78)
Удельные нормальные давления при вдавливании резца на задней грани резца σN:
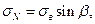 (79)
(79)
где σв – нормальное удельное давление при вдавливании резца в породу:
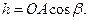
Тогда:
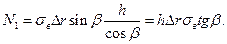 (80)
(80)
Подстановка N1 из (80) в (78) дает:
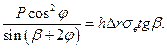 (81)
(81)
Решая относительно h имеем:
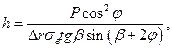 (82)
(82)
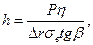 (83)
(83)
где:
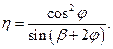 (84)
(84)
Угол трения резца о породу φ находится в пределах от 15 до 25°, значения коэффициента η колеблются в пределах от 0,93 до 0,97.
Формула (83) позволяет теоретически определить глубину внедрения резца в породу, которая возрастает при увеличении нагрузки Р, и снижается при увеличении прочности пород σв; чем меньше угол приострения β, тем глубже величина h.
Из формулы (83) следует, что уменьшение угла заточки резца β способствует росту механической скорости бурения. В практике угол β лежит в пределах 60-80°. При малых углах β наблюдаются сколы острых граней при встрече твердых включений.
В расчетной формуле (83) величина σв характеризует прочность породы. Если резец вдавливается в породу без вращения, то эта схема аналогична схеме вдавливания пуансона. Тогда за величину σв можно принять с достаточной степенью достоверности твердость породы по штампу – Рш.
В практике бурения внедрение резца в породу забоя осуществляется при вращении породоразрушающего инструмента и при уменьшенных усилиях Р. Предложенная схема рассмотрения внедрения резца этот фактор не учитывает, поэтому позволяет получить лишь качественную картину взаимодействия резца с породой забоя. После того как резец внедрен в породу, предложенная схема рассматривает процесс движения резца в горизонтальной плоскости. В начальный период движения резца передняя грань сминает (раздавливает) породу, после чего в упруго-пластичных и хрупких породах происходит ее скол. В зависимости от характера разрушения в расчетную формулу (83) вводятся различные значения сопротивления горных пород смятию или сколу. В установившемся режиме работы резца порода разрушается последовательно в двух стадиях, смятие породы – скол.
Для изучения работы породоразрушающего инструмента режущего типа первостепенный интерес представляет эпюра реакции забоя. Рассмотрим этот вопрос для лопастного долота, лопасть которого – пластина толщиной δ и диаметром D (D = 2R, R – радиус) В.С. Владиславлев установил, что контактное давление под лопастью долота распределяется крайне неравномерно, в центральной части имеют место максимальные давления, но именно в центре лезвия горизонтальная скорость вращения лопасти равна нулю (υокр = 0). Это обстоятельство является причиной того, что именно центральная часть забоя наиболее трудно поддается разрушению, в результате чего механическая скорость бурения падает. Для снижения такого негативного эффекта к центральной части лопастных долот делают вырез, а образующийся при этом в этой зоне столбик горной породы периодически скалывается в результате поперечной вибрации долота. На рис. 20 и 21 показано распределение интенсивности нагрузки под лопастным долотом с рассечкой и без нее. Долото снабжено центральным вырезом, который позволяет снизить энергоемкость разрушения горных пород и повысить механическую скорость бурения.
Теоретически эпюра контактных давлений (qi) описывается уравнением гиперболы:
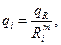 (85)
(85)
где qR – контактное давление на расстоянии R от оси долота; т – показатель степени, определяется экспериментально, 0 < m < 1,5.
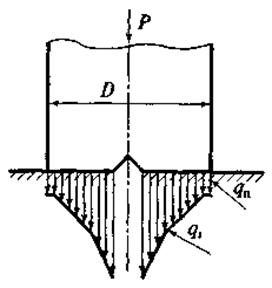
Рис. 20. Распределение интенсивности нагрузки под лопастным долотом
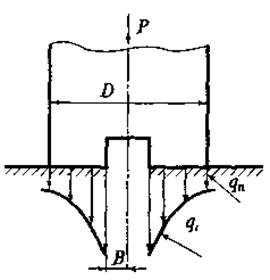
Рис. 21. Распределение интенсивности нагрузки под лопастным долотом с рассечкой
Эксплуатация лопастных долот характеризуется неравномерным износом рабочих лопастей – более интенсивным износом периферийных участков. Традиционно этот недостаток компенсируется более мощным вооружением периферийных участков лопастей долота либо киданием долота, у которого бы рабочие лопасти изнашивались равномерно по длине.
Износ рабочих органов долота пропорционален работе сил трения:
qi υi = const, (86)
где υi – окружная скорость пропорциональна диаметру долота и угловой частоте вращения.
Расчет по формуле (86) затрудняется не только тем, что для различных пар долото – горная порода требуется экспериментально определять значения qi, но и тем, что коэффициент трения (сопротивления) также не является величиной постоянной и зависит не только от контактных усилий, но и от окружной скорости. Геометрия лопастей с равномерным износом имеет конусообразную форму и с достаточной степенью точности описывается уравнением гиперболы.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 407; Нарушение авторских прав?; Мы поможем в написании вашей работы!