Составление алгоритма решения

Составление алгоритма решения – завершающий этап алгоритмизации, однозначно определяющий, с учётом выбранного метода решения, путь преобразования математической модели задачи в результаты.

Составить алгоритм – значит выбрать единственный из всех возможных вариантов решения.

Алгоритм – совокупность предписаний, однозначно и подетально определяющих последовательность преобразования исходных данных в конечные результаты.

Основные свойства алгоритма:

· определённость;

· массовость;

· результативность;

· дискретность.

Определённость означает однозначность выполнения запланированной последовательности элементарных действий.

Определённость исключает нарушения заданного порядка вычислений и произвольность толкования предписаний.

Массовость определяет возможность применения для различных задач одного класса.

Массовость достигается реализацией в алгоритме конкретной задачи её универсального математического описания.

Результативность характеризует неизбежность получения конкретного результата при выполнении алгоритма.

Результатом могут быть выходные данные или сообщение о невозможности решения задачи.

Дискретность означает представление в виде совокупности фрагментов, элементарных действий.

Дискретность определяет обязательную детализацию алгоритма.

Основные качества алгоритма:

· наглядность;

· информативность.

Наглядность – обеспечение простоты, доступности восприятия алгоритма в целом.

Информативность – представление максимума детализированных сведений о технологии решения задачи.

Алгоритм составляется для человека, поэтому должен быть относительно простым (наглядным) и достаточно информативным. Компромисс между этими требованиями достигается выбором степени детализации. Например, замена несложной формулы несколькими простыми увеличивает информативность, но делает алгоритм громоздким, менее наглядным. Укрупнение действий улучшает наглядность, но ухудшает информативность.

Существуют различные способы представления алгоритмов, чаще используют два из них:

· словесное описание;

· графическое изображение (схема алгоритма).

Словесное описание алгоритма – последовательность конкретных указаний на разговорном языке, приводящая к решению задачи.

Так, для задачи о картофеле (пример 2.3) на основании составленной математической модели и выбранного численного метода решения можно предложить следующее словесное описание алгоритма:

1) Начать решение.

2) Ввести исходные данные ПД, ПШ, УБ, ПО, k₁, k₂, k₃, k₄.

3) Вывести исходные данные ПД, ПШ, УБ, ПО, k₁, k₂, k₃, k₄.

4) Вычислить площадь поля .

5) Вычислить массу выращенного картофеля .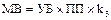

6) Вычислить массу потерь картофеля .

7) Вычислить товарную массу картофеля МТ = МВ – МП.

8) Вывести на печать результаты ПП, МВ, МП, МТ.

9) Закончить решение.

Вывод исходных данных выполняется для контроля правильности их ввода.

Основные недостатки словесного способа – громоздкость и отсутствие наглядности при описании сложных алгоритмов. Поэтому в большинстве случаев используется способ представления алгоритма в виде графической схемы.

Схема алгоритма – совокупность геометрических фигур (блоков), обозначающих (определяющих) запланированный путь решения задачи.

Блоки – элементы схемы, обозначающие стандартные предписания (действия) в алгоритме.

Например, ввод, вывод, вычисление по формулам, проверка условий. В схеме блоки соединяются линиями связи, определяющими последовательность их выполнения.

Обозначения, наименования и правила использования блоков определяются ГОСТом (табл. 1.3).

Таблица 1.3

Наименование	Обозначение	Пояснение
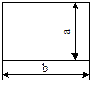
Процесс		Обозначение вычислений по одной или нескольким формулам, записываемым внутри блока. Имеет один вход и один выход
Решение		Проверка записанного в блоке условия, в результате чего выбирается тот или иной путь решения задачи. Имеет один вход и 2 (несколько) выходов
Ручной ввод		Ввод данных, указанных в блоке. Имеет один вход и один выход

Продолжение табл. 1.3

Наименование	Обозначение	Пояснение
Документ		Вывод указанной в блоке информации на бумажный носитель. Имеет один вход и один выход
Дисплей		Вывод указанной в блоке информации на экран дисплея. Имеет один вход и один выход
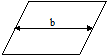
Ввод, вывод		Общий вид операции ввода/вывода информации. Имеет один вход и один выход
Модификация		Начало цикла с параметрами, записанными внутри блока. Имеет два входа и два выхода
Предопре-делённый процесс		Переход к подпрограмме с возвратом из неё. Имеет один вход и один выход
Начало цикла		Общее обозначение начала цикла. Имеет один вход и один выход
Конец цикла		Общее обозначение окончания цикла. Имеет один вход и один выход

Окончание табл. 1.3

Наименование	Обозначение	Пояснение
Запоминающее устройство с прямым доступом		Запись (считывание) данных. Носитель данных – магнитный диск. Имеет один вход и один выход
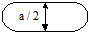
Пуск, останов		Начало (конец) в основном алгоритме или вход (выход) в дополнительном
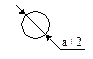
Соединитель		Обозначение разрывов соединительных линий алгоритма, расположенных на одной или разных страницах
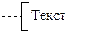
Комментарий		Обозначение, примыкающее к блоку, содержимое которого требуется пояснить, расшифровать

В качестве вертикального размера блоков рекомендуется использовать значения ряда 10, 15, 20 мм с допускаемым увеличением на число, кратное 5.

Горизонтальный размер b рекомендуется выбирать в полтора раза большим, чем a (). При выполнении схем вручную допускается соотношение 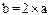. В одной схеме возможно использование блоков не более чем с двумя размерами а.

В верхней левой части блоков в разрыве контура записываются их порядковые номера. Основные направления построения схемы – вниз и вправо. На линиях, соединяющих блоки в схему, стрелки указываются на направлениях, противоположных основным, т.е. снизу вверх и справа налево.

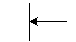
Пересечение линий связи нежелательно. Если этого избежать нельзя, пересекающиеся линии считаются не имеющими логической связи. Соединение (состыковка) двух линий возможна (табл. 1.4).

Таблица 1.4

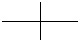
Примеры пересечения линий
не соединяющиеся	соединяющиеся слева	соединяющиеся справа

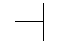
При необходимости изображения других вариантов соединяющихся линий требуется руководствоваться следующими примерами (табл. 1.5).

Таблица 1.5

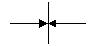
Соединение	правильное	неправильное
с передачей управления вниз:
с передачей управления вверх: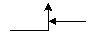

Минимальное расстояние между параллельными линиями связи 3 мм, между блоками – 5 мм. При разрыве линии связи на концах разрыва размещаются соединители. Оба соединителя имеют одинаковую маркировку, например, номер блока, которому передаётся управление. Если соединители расположены на разных страницах, каждый дополняется комментарием. Например:

С учётом изложенного выполним простейшую схему алгоритма задачи о картофеле (пример 1.3) при выбранной в модели степени детализации (рис. 1.4).

Рис. 1.4. Простейшая схема алгоритма задачи о картофеле

Рекомендации по эффективным методам составления алгоритмов приведены в разделе 2.3.

Дата добавления: 2014-01-07