Метод начальных параметров

Метод непосредственного интегрирования удобен в том случае, когда количество участков в балке 1 или 2. Если количество участков в балке больше двух, то удобнее пользоваться методом начальных параметров.

При выводе уравнений начальных параметров необходимо пользоваться следующими правилами:

1. Начало координат выбирается в крайней левой точке балки и считается постоянным для всех участков.

2. Если в сечении действует сосредоточенный момент М, то в выражение для изгибающих моментов он вводится с сомножителем (x – a) ⁰, где a – расстояние от начала координат до точки приложения сосредоточенного момента.

3. Если распределенная нагрузка не доходит до конца балки, то её продолжают до конца балки и вводят компенсирующую нагрузку такой же интенсивности.

4. Интегрирование дифференциального уравнения ведется без раскрытия скобок.

5. При составлении выражения для изгибающего момента (M_x) учитываются только те силы, которые расположены слева от рассматриваемого сечения х.

Рассмотрим балку длиной l (рис. 18.4.1) с пятью участками.

Рис. 18.4.1

Жесткость балки EI_z..

Начало координат выберем на левом конце балки – т. О. Так как нагрузка не доходит до конца балки, то продолжим её и введем компенсирующую (т. е. обратного направления) нагрузку такой же интенсивности (покажем её пунктиром).

Составим дифференциальное уравнение упругой линии балки для пятого участка:

Проинтегрировав его дважды, получим, соответственно, уравнение углов поворота и прогибов для пятого участка:

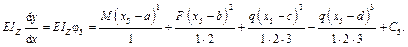
Составим дифференциальное уравнение упругой линии балки для остальных участков:

– для IV участка:

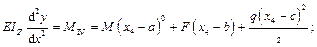
– для III участка:

– для II участка:

– для I участка:

.

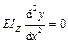Определим физический смысл постоянных интегрирования С и D. Для этого проинтегрируем дважды дифференциальное уравнение упругой линии балки на участке:

; .

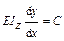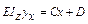Если x = 0, то 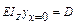; , т. е. обозначим; 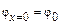, где φ₀, y ₀ – соответственно угол поворота и прогиб в начале координат.

Тогда для I участка уравнение можно переписать в виде:

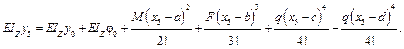
Уравнения на остальных участках отличаются только количеством слагаемых, тогда можно записать универсальные уравнения начальных параметров (18.4.1); (18.4.2):

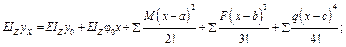(18.4.1)

, (18.4.2)

где y ₀, φ₀ – прогиб и угол поворота в начале координат (начальные параметры), определяются из граничных условий; – расстояние от начала координат до рассматриваемого сечения;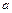,,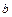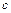– расстояние от начала координат до M, F, 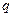соответственно (рис. 18.4.1); M, F, 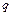– нагрузки, включая реактивные.

Знак перед слагаемыми ставится в соответствии со знаком изгибающего момента.

Пример 18.4.1. Определить прогиб сечения С, угол поворота сечения В для балки (рис. 18.4.2), если EI_z = const, F = 4 кН; М = 5 кНм,

q = 2 ^кН/_м. Сечение балки: двутавр № 20. I_z = 1840 см⁴.

  Рис. 18.4.2

Решение. Определим реакции опор:

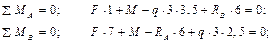
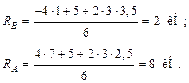
Проверка: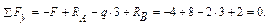

Рис. 18.4.3

«Подготовим» балку для использования универсальных уравнений метода начальных параметров (рис. 18.4.3), т. е.

– начало координат выберем на крайнем левом конце балки;

– распределенную нагрузку продлим до конца балки и введем компенсирующую нагрузку.

Запишем граничные условия, физический смысл которых заключается в том, что прогибы в опорных сечениях равны нулю:

а) x = 1 м; y = 0;

б) x = 7 м; y = 0.

Из граничных условий определим начальные параметры (y ₀; φ₀). Для этого подставим в универсальные уравнения (18.4.1) граничные условия:

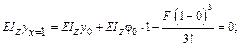
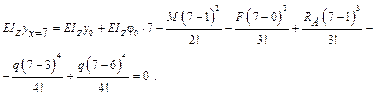
Решаем полученную систему уравнений:

;

.

Определим прогиб сечения С, подставив в уравнение (18.4.1) 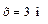, рассматривая только ее силы, которые расположены слева от этого сечения:

.

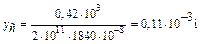Знак «плюс» показывает, что сечение С перемещается вверх. Определим угол поворота сечения В, подставив в уравнение (18.4.2) :

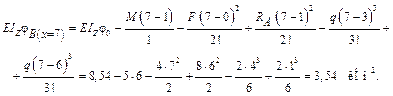
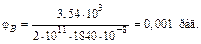
Знак «плюс» показывает, что сечение В поворачивается против часовой стрелки.

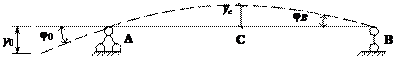
Определим значения угла поворота и прогиба в начале координат:

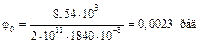(поворот по часовой стрелке);

(прогиб вниз).

Покажем упругую линию балки (рис. 18.4.4).

Дата добавления: 2014-01-07