Астрономические методы определения скорости света

Классические опыты по измерению скорости света

Эффект Доплера в оптике

Экспериментальные основания специальной теории относительности

Современные методы измерения скорости света

Распространение света в движущихся средах

Классические опыты по измерению скорости света

Задача определения скорости света принадлежит к числу важнейших проблем оптики и физики вообще. Решение этой задачи имело огромное принципиальное и практическое значение. Установление того, что скорость распространения света конечна, и измерение этой скорости сделали более конкретными и ясными трудности, стоящие перед различными оптическими теориями. Первые методы определения скорости света, опиравшиеся на астрономические наблюдения, способствовали со своей стороны ясному пониманию чисто астрономических вопросов. Точные лабораторные методы определения скорости света, выработанные в последствии, используются при геодезической съёмке.

Основная трудность, на которую наталкивается экспериментатор при определении скорости распространения света, связана с огромным значением этой величины, требующим совсем иных масштабов опыта, чем те, которые имеют место в классических физических измерениях. Эта трудность дала себя знать в первых научных попытках определения скорости света, предпринятых ещё Галилеем (1607 г.). Опыт Галилея состоял в следующем: два наблюдателя на большом расстоянии друг о

друга снабжены закрывающимися фонарями. Наблюдатель А открывает фонарь; через известный промежуток времени свет дойдет до наблюдателя В, который в тот же момент открывает свой фонарь; спустя определенное время этот сигнал дойдет до А, и последний может, таким образом, отметить время τ, протекшее от момента подачи им сигнала до момента его возвращения. Предполагая, что наблюдатели реагируют на сигнал мгновенно и что свет обладает одной и той же скоростью в направлении АВ и ВА, получим, что путь АВ + ВА =2 D свет проходит за время τ, т.е. скорость света с =2 D / τ. Второе из сделанных допущений может считаться весьма правдоподобным. Современная теория относительности возводит даже это допущение в принцип. Но предположение о возможности мгновенно реагировать на сигнал не соответствует действительности, и поэтому при огромной скорости света попытка Галилея не привела ни к каким результатам; по существу, измерялось не время распространения светового сигнала, а время, потраченное наблюдателем на реакцию. Положение можно улучшить, если наблюдателя В заменить зеркалом, отражающим свет, освободившись таким образом от ошибки, вносимой одним из наблюдателей. Эта схема измерений осталась, по существу, почти во всех современных лабораторных приемах определения скорости света; однако впоследствии были найдены превосходные приемы регистрации сигналов и измерения промежутков времени, что и позволило определить скорость света с достаточной точностью даже на сравнительно небольших расстояниях.

а) Метод Рёмера.

Юпитер имеет несколько спутников, которые либо видны с Земли вблизи Юпитера, либо скрываются в его тени. Астрономические наблюдения над спутниками Юпитера показывают, что средний промежуток времени между двумя последовательными затмениями какого-нибудь определённого спутника Юпитера зависит от того, на каком расстоянии друг от друга находятся Земля и Юпитер во время наблюдений.

Метод Рёмера (1676 г.), основанный на этих наблюдениях, можно пояснить с помощью рис.9.1. Пусть в определённый момент времени Земля З ₁ и Юпитер Ю ₁ находятся в противостоянии и в этот момент времени один из спутников Юпитера, наблюдаемый с Земли, исчезает в тени Юпитера. Тогда, если обозначить через R и r радиусы орбит Юпитера и Земли и через с – скорость света в системе координат, связанной с Солнцем, на Земле уход спутника в тень Юпитера будет зарегистрирован на секунд позже, чем он совершается во временной системе отсчёта, связанной с Юпитером.

По истечении 0,545 года Земля З ₂ и Юпитер Ю ₂ находятся в соединении. Если в это время происходит n -е затмение того же спутника Юпитера, то на Земле оно будет зарегистрировано с опозданием на 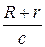секунд. Поэтому, если период обращения спутника вокруг Юпитера t, то промежуток времени T ₁, протекший между первым и n -м затмениями, наблюдавшимися с Земли, равен

Рис. 9.1. К определению скорости света по методу Рёмера.

.

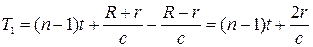По истечении ещё 0,545 года Земля З ₃ и Юпитер Ю ₃ будут вновь находиться в противостоянии. За это время совершились (n –1) оборотов спутника вокруг Юпитера и (n –1) затмений, из которых первое имело место, когда Земля и Юпитер занимали положения З ₂ и Ю ₂, а последнее – когда они занимали положение З ₃ и Ю ₃. Первое затмение наблюдалось на Земле с запозданием 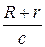, а последнее с запозданием по отношению к моментам ухода спутника в тень планеты Юпитера. Следовательно, в этом случае имеем:

.

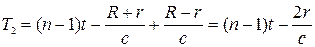Рёмер измерил промежутки времени Т ₁ и Т ₂ и нашёл, что Т ₁– Т ₂=1980 с. Но из написанных выше формул следует, что Т ₁– Т ₂=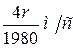, поэтому . Принимая r, среднее расстояние от Земли до Солнца, равным 150·10⁶ км, находим для скорости света значение: с =301·10⁶ м/с.

Этот результат был исторически первым измерением скорости света.

б) Определение скорости света по наблюдению аберрации.

В 1725-1728 гг. Брадлей предпринял наблюдения с целью выяснить, существует ли годичный параллакс звёзд, т.е. кажущееся смещение звёзд на небесном своде, отображающее движение Земли по орбите и связанное с конечностью расстояния от Земли до звезды. Звезда в своём параллактическом движении должна описывать эллипс, угловые размеры которого тем больше, чем меньше расстояние до звезды.

Для звёзд, лежащих в плоскости эклиптики, этот эллипс вырождается в прямую, а для звёзд у полюса – в окружность. Брадлей действительно обнаружил подобное смещение. Но большая ось эллипса оказалась для всех звёзд имеющие одни и те же угловые размеры, а именно 2 α =40",9. Брадлей объяснил (1728 г.) наблюдённое явление, названное им аберрацией света, конечностью скорости распространения света и использовал его для определения этой скорости. Годичный параллакс был установлен более ста лет спустя В.Я. Струве и Бесселем (1837, 1838 гг.).

Для простоты будем вместо телескопа пользоваться визирным приспособлением, состоящим из двух небольших отверстий, расположенных по оси трубы. Когда скорость Земли совпадает по направлению с SE, ось трубы указывает на звезду. Когда же скорость Земли (и трубы) составляет угол j с направлением на звезду, то для того, чтобы луч света оставался на оси трубы, трубу надо повернуть на угол a (рис. 9.2), ибо за время t, пока свет проходит путь SE, сама труба перемещается на расстояние E'Е = u ₀ t. Из рис. 9.2 можно определить поворот a. Здесь SE определяет направление оси трубы без учёта аберрации, SE' – смещенное направление оси, обеспечивающее прохождение света вдоль оси трубы в течение всего времени t. Пользуясь тем, что угол a очень мал, так как u ₀<<с (пренебрегая членами порядка ), можно считать, что

Ð SE'Р» Ð SEP = j.

Тогда из треугольника E'SE получаем

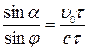или .

Если звезда лежит в плоскости эклиптики, то направление вектора скорости Земли u ₀ меняется по отношению к направлению на звезду (ES) в течение года по закону 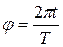, где Т — период обращения Земли, и зависимость угла аберрации от времени выражается периодической функцией .

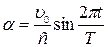Рис. 9.2. К вычислению аберрационного смещения.

Таким образом, направление на звезду меняется периодически в течение года: звезда совершает кажущееся колебания с угловой амплитудой около среднего положения, соответствующего значению j =0 или p.

Если звезда находится в полюсе эклиптики, то j =90° в течение всего года, т.е. угловое отклонение звезды сохраняется неизменным по величине (); но так как направление вектора u ₀ изменяется в течение года на угол 2 p, то и угловое смещение звезды меняется по направлению: звезда описывает кажущуюся круговую орбиту с угловым радиусом .

В общем случае, когда звезда расположена на угловом расстоянии d от плоскости эклиптики, аберрационная траектория звезды представляет собой эллипс, большая полуось которого имеет угловые размеры a ₀, а малая – a ₀sin d. Именно такой характер и носило кажущееся смещение звёзд по наблюдению Брадлея. Определив из наблюдений a ₀ и зная u ₀, можно найти с. Брадлей нашёл с =308 000 км/с. В. Я. Струве (1845 г.) значительно улучшил точность наблюдений и получил a ₀=20",445. Самые последние определения дают a ₀=20",470, чему соответствует с =299 900 км/с.

Следует отметить, что аберрация света связана с изменением направления скорости Земли в течение года.

Дата добавления: 2014-01-07