
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры организации циклов
|
|
|
|
Пример 1.13.1. Вычислить сумму членов степенного ряда
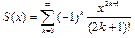
с точностью 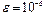 .
.
Рассмотрим математическую сторону задачи. Пусть 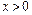 . Погрешность суммы членов
. Погрешность суммы членов 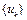 знакочередующегося ряда не превосходит модуля первого отброшенного члена. Тогда условия выполнения тела цикла имеет вид
знакочередующегося ряда не превосходит модуля первого отброшенного члена. Тогда условия выполнения тела цикла имеет вид 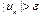 . Из отношения двух последовательных членов получаем рекуррентную формулу
. Из отношения двух последовательных членов получаем рекуррентную формулу
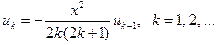 , причем
, причем 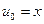 .
.
Реализующая программа имеет вид (в частности, при 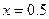 ):
):
| program sample_1_13_1 real(4):: x=0.5, u, s, y integer(4) k y=-x**2; u=x; s=u; k=2 do while(abs(u)>1.e-6) u=u*y/(k*(k+1)); s=s+u; k=k+2 end do print *,’s=’,s end |
Результаты расчета:
s= 0.4794255
Пример 1.13.2. Вычислить сумму членов ряда
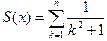
Реализующая программа имеет вид (задано 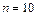 ):
):
| program sample_1_13_2 real(4):: s=0 integer(4) k,n print *,’ Vvedite n’ read *,n do k=1,n s=s+1./(k**2+1) end do print 1,n,s 1 format(/2x,’Kolichestvo uchitivaemikh chlenov ryada n=’,i3,& /2x,’Iskomaya summa ryada s=’,g12.4) end |
Результаты расчета:
Kolichestvo uchitivaemikh chlenov ryada n= 10
Iskomaya summa ryada s= 0.9818
Пример 1.13.3. Вычислить сумму членов ряда
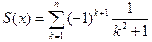
Реализующая программа имеет вид (задано 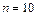 ):
):
| program sample_1_13_3 real(4):: znak,s=0 integer(4) k,n print *,’ Vvedite n’ read *,n k=1; znak=(-1)**(k+1) do k=1,n s=s+znak/(k**2+1) znak=-znak end do print 1,n,s 1 format(/2x,’Kolichestvo uchitivaemikh chlenov ryada n=’,i3,& /2x,’Iskomaya summa ryada s=’,g12.4) end |
Результаты расчета:
Kolichestvo uchitivaemikh chlenov ryada n= 10
Iskomaya summa ryada s= 0.3595
По представленным текстам последних двух программ (примеры 1.13.2 и 1.13.3) необходимо сделать ряд пояснений:
1. Математическому выражению 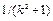 соответствует выражение на Фортране
соответствует выражение на Фортране 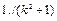 . Константа 1. имеет вещественный тип, поэтому результат деления будет также вещественным (в этом случае дробная часть не отбрасывается). При записи заданного выражения на Фортране в виде
. Константа 1. имеет вещественный тип, поэтому результат деления будет также вещественным (в этом случае дробная часть не отбрасывается). При записи заданного выражения на Фортране в виде 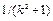 его результат для
его результат для 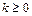 будет всегда нулевым, т.к. константа 1 имеет целый тип, и, следовательно, результат деления также будет целого типа (дробная часть отбрасывается).
будет всегда нулевым, т.к. константа 1 имеет целый тип, и, следовательно, результат деления также будет целого типа (дробная часть отбрасывается).
2. Введение переменной znak для вычисления величины 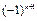 делает вычислительный процесс более экономичным, т.к. фактически выражение
делает вычислительный процесс более экономичным, т.к. фактически выражение 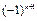 принимает только два значения (1 и -1). К тому же переменная znak имеет вещественный тип, и, следовательно, результат деления будет также вещественного типа (сохраняется дробная часть).
принимает только два значения (1 и -1). К тому же переменная znak имеет вещественный тип, и, следовательно, результат деления будет также вещественного типа (сохраняется дробная часть).
Пример 1.13.4. Требуется запросить у пользователя семь произвольных вещественных чисел и подсчитать их сумму. Однако если будет введено отрицательное число, следует прекратить подсчет и вывести имеющуюся сумму на экран.
Реализующая программа имеет вид (задано 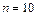 ):
):
| program sample_1_13_4 real(4):: x,s=0. integer(4):: i,n=7 do i=1,n print *,’Vvedite chislo’ read *,x print *,’ Vvedennoe znachenie chisla =’,x if(x<0.) exit! Если число отрицательное, то выход из цикла s=s+x end do print *,’ Summa s=’,s end |
Результаты расчета:
Vvedennoe znachenie chisla = 5.000000
Vvedennoe znachenie chisla = 5.000000
Vvedennoe znachenie chisla = 3.000000
Vvedennoe znachenie chisla = 10.00000
Vvedennoe znachenie chisla = 5.000000
Vvedennoe znachenie chisla = -8.000000
Summa s= 28.00000
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 298; Нарушение авторских прав?; Мы поможем в написании вашей работы!