Конспект лекций

ЛЕКЦИЯ №3. РАССЛЕДОВАНИЕ И УЧЕТ ХРОНИЧЕСКИХ ПРОФЕССИОНАЛЬНЫХ ЗАБОЛЕВАНИЙ И ОТРАВЛЕНИЙ……43

СПЕЦИАЛЬНЫЕ РАЗДЕЛЫ ОХРАНЫ ТРУДА В ОТРАСЛИ ПРОФЕССИОНАЛЬНОЙ ДЕЯТЕЛЬНОСТИ …………………………45

ЛЕКЦИЯ №4. Проблемы физиологии, гигиены труда и производственной санитарии в отраслях промышленности, где используется современное компьютерное оборудование ………………………………….………….......................45

4.1.Основные вредные производственные факторы, воздействующие на организм пользователя ПК и других видов оргтехники………………………………………………………………………..50

4.2. Микроклимат помещения и состояние здоровья………....…………51

4.3.Лазерное излучение…………...………………………………………...53

Лекция №5. Заболевания наиболее характерные для работников, использующих в повседневной практике и быту различную оргтехнику……………………………………………...54

5.1. Сотовый телефон и безопасность здоровья……………...................64

ЛЕКЦИЯ №6 Мероприятия по улучшению состояния производственной сферы, где широко используется современное компьютерное оборудование………………………68

6.1.Обеспечение необходимого микроклимата в помещениях с ПК…………………………………………………………………………………70

6.2.Электростатистические поля………………………………………………..70

6.3. Требования к уровням шума……………………………………………….72

6.4. Электромагнитные излучения………………………………………...........72

6.5. Обустройство рабочих мест с ПК………………………………...………..73

6.6. Компьютерные очки…………………………………………………...........75

6.7. Организация режима труда и отдыха пользователей ПК……………… 76

6.8. Требования к организации медицинского обслуживания пользователей ВДТ и ПЭВМ………………………………………………...…………………..77

6.9.Основные требования ТБ при работе с персональным компьютером……………………………………………………………………..82

6.10.Как легко снимать усталость при работе за копьютером………………………84

ЛЕКЦИЯ № 7. ОСНОВНЫЕ МЕРОПРИЯТИЯ ПО ПОЖАРНОЙ ПРОФИЛАКТИКЕ НА ОТРАСЛЕВЫХ ОБЪЕКТАХ…………………….....103

7.1. Категории помещений и зданий и классы зон по пожарной и взрывной опасности……………………………………………..……………..103

ЛЕКЦИЯ № 8. СОЦИАЛЬНОЕ СТРАХОВАНИЕ ОТ НЕСЧАСТНОГО СЛУЧАЯ И ПРОФЕССИОНАЛЬНОГО ЗАБОЛЕВАНИЯ НА ПРОИЗВОДСТВЕ……………………………………………………………..111

8.1. Система финансирования и источники средств Фонда социального страхования от несчастных случаев…………………………………………..125

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ………………………...129

СОДЕРЖАНИЕ……………………………………………………………….131

по курсу «математические задачи электроэнергетики»

В.Г. Бугров

Предисловие

Цель курса МЗЭ - связать математику как общетеоретическую дисциплину с практическими ее применениями в работе инженера и дать конкретный практический аппарат для инженерных исследований. При этом очень важно исходить из положения, что под настоящей «математической культурой» надо понимать умение дать правильную оценку того, что математика может и чего она не может, каковы границы применения различных методов, что понимать под строгостью и точностью в инженерно-математических задачах. Роль математики в решении различных задач, всегда имевшая огромное значение, возросла еще больше с появлением вычислительной техники. Однако эта роль не должна преувеличиваться, так как может привести к потере правильной ориентировки инженера, что очень опасно. Инженеру следует помнить, математическими соотношениями, в частности дифференциальными уравнениями, можно описать все, что угодно, если только принять определенные постулаты. Можно при этом получить соответствующим расчетом м а т е м а т и ч е с к и а б с о л ю т н о с т р о г и е результаты, не имеющие н и к о к о г о р е а л н о г о с м ы с л а для инженера. Нужно помнить, что прежде чем математический аппарат может быть использован для изучения реального и во всех смыслах бесконечно сложного явления, необходимо это явление подвергнуть предварительному анализу, выделив из него «главную часть», которая представляет интерес в данной задаче. Это и будет основная его модель.

Создание моделей, отвечающих экспериментально проверенным условиям целей исследования всегда остается центральной задачей математика и математики. Отступление от идеи «реальной модели» исследования могут приводить инженера к ошибкам, а теоретика - к нелепым выводам и обобщениям, якобы «с т р о г и м».

(В свое время была опубликована одна «научная работа», в которой ставился и математически вполне «строго» исследовался вопрос о том, «почему приведения появляются только в старинных замках?». Объяснение основано на формально правильном использовании квантово-механической формулы для прозрачности потенциальных барьеров при соответствующих «абсолютно строгих» решениях на ЭВМ. Известно, что прозрачность потенциального барьера экспоненциально убывает с увеличением его толщины, завися от массы частицы, проходящей сквозь барьер. Приписав приведению некоторую небольшую массу, можно получить для него довольно высокую прозрачность барьеров, соответствующих стенам современных домов и, напротив, низкую прозрачность толстых наружных стен старинных замков. Поэтому в старинном замке приведение находится как бы в ловушке и существует веками.

Вместе с тем малая масса приведения делает его очень чувствительным к ударам частиц света (фотонам) при попутке осветить приведение. Отраженный от приведения фотон отдает ему большую часть своей энергии и становится маленьким фотоном невидимого излучения. Поэтому приведения видны только в полумраке.)

В инженерных задачах точность часто смешивается со строгостью. Понятие инженерной строгости вытекает из поставленных при исследовании целей и определяется этой постановкой задачи и необходимостью получения после ее решения нужных для практики результатов.

Наиболее важными специальными задачами электрических систем, для которых инженер должен усвоить аппарат решения являются очевидно следующие:

1) некоторые приемы определения вероятностей;

2) способы анализа некоторых дифференциальных уравнений, используемых при выяснения устойчивых состояний систем.

3) анализ электрических цепей с понятием о методах теории графов;

4) методы принятия решений.

Раздел 1

ПРИМЕНЕНИЕ МЕТОДОВ ТЕОРИИ ВЕРОЯТНОСТЕЙ В ЗАДАЧАХ ЭЛЕКТРОЭНЕРГЕТИКИ

1-1. ПОСТАНОВКА ЗАДАЧИ

Теория вероятностей—это математическая наука, изучающая· закономерности случайных событий, случайных величин и случайных функций. Рассмотрим значение термина «случайный» применительно к событиям, величинам и функциям. I

Каждое событие, происходящее в окружающем мире, является результатом воздействия большого числа других событий, влияю­щих на возможность возникновения данного события. Случайным событием называется событие, которое может в данных конкретных условиях или произойти, или не произойти. В отличие от этого достоверным называется событие, которое обязательно произойдет, а невозможным — событие, которое не может произойти. Что дает основание считать то или иное событие случайным, достоверным или невозможным?

Только опыт или наблюдения за событиями могут привести к каким-либо выводам. Однако опыт или наблюдения должны быть при этом достаточно длительными, иначе суждение о том, что собы­тие является случайным, достоверным или невозможным, может оказаться ошибочным. Только при достаточно большом количестве наблюдений за данным событием можно установить, является ли вообще данное событие случайным.

Естественно, возникает вопрос, существуют ли закономерности у случайных событий? Не являются ли понятия «закономерность» и «случайность» взаимно исключающими? Нет, эти понятия диалек­тически связаны между собой и не исключают друг друга. Про­изойдет ли в данном случае или не произойдет случайное событие, определяется совокупностью большого числа причин, которые в большенстве случаев практически нельзя проанализировать, но все же случайное событие происходит или не происходит вполне законо­мерно.

Так как невозможно проанализировать все причины, влияю­щие на возникновение случайного события, то и невозможно с до­стоверностью предсказать, произойдет оно или нет в данном конк­ретном случае. Если же рассматривать достаточно большое число случаев, когда событие может произойти или не произойти, или производить большое число проб (испытаний), то у любого случай­ного события начнет проявляться определенная объективная зако­номерность.

Давно было замечено, что если многократно наблюдать то или иное случайное событие, то относительная частота его возникновения, т. е. отношение числа случаев, когда событие происходит, к общему числу наблюденных случаев по мере увеличения их числа и при полной одинаковости условий, влияющих на возникновение данного собы­тия, слабо колеблется относительно некоторой постоянной величины, причем чем больше число наблюденных случаев, тем меньше размер этих колебаний. Устойчивость относительной частоты возникновения случайного события при значительном числе наблюденных случаев (испытаний) дает основание считать, что та величина, около кото­рой колеблется относительная частота, характеризует объективную возможность осуществления данного случайного события. Эта вели­чина в теории вероятностей называется вероятностью события. Таким образом, закономерность случайного события, определяемая его вероятностью, проявляется при достаточно большом числе наблю­дений или испытаний, т. е. на основе анализа большого статисти­ческого материала. Это обстоятельство является очень важным, так как попытки определить вероятность случайных событий при очень малом числе наблюдений могут привести к серьезным ошибкам вплоть до признания случайного события достоверным или невоз­можным.

Случайной величиной называется величина, принимающая в ре­зультате опыта то или иное значение (это значение неизвестно заранее). Между случайной величиной и случайным событием существует тесная связь. Если каждому случайному событию можно поставить в соответствие какую-либо величину, то появлению того или иного случайного события соответствует та или иная случайная величина. В качестве случайной величины можно принять и число однород­ных случайных событий за определенный промежуток времени. Слу­чайные величины отличаются от обычных (неслучайных) величин тем, что в разных случаях (или испытаниях) значения их могут быть разными. Однако все случайные величины подчинены тем или иным объективным закономерностям. Так, например, они могут иметь ограниченные области возможных значений; различные значения случайных величин могут иметь различные вероятности. Заметим, что к числу случайных величин относятся такие величины, как ошибки измерения, ошибки прогнозирования и т. п.

Случайной функцией называется величина, изменяющаяся при изменении аргумента случайным образом. В отличие от обычной (неслучайной) функции, имеющей определенные значения при определенном значении аргумента, случайная функция при заданном значении аргумента является случайной величиной, т. е. может иметь различные значения е различной их вероятностью.

Если аргументом случайной функции, как это в большинстве практических приложений имеет место, является время, то такая случайная функция называется случайным процессом.

В каждом отдельном опыте случайная функция имеет некоторое конкретное значение. Случайная функция в каждом отдельном οпыте представляется некоторой конкретной функцией аргумента –неслучайной. Эта конкретная функция называется реализацией случайной функции в данном опыте. Реализацией случайного процесса в данном опыте называется, очевидно, некоторая конкретная функция времени, наблюденная в данном опыте. Итак, реализацией случайной функции (случайного процесса) является неслучайная функция аргумента (времени), наблюденная в данном опыте. В дальнейшем будет paссматриваться главным образом случайный процесс, являющийся частным случаем случайной функции, так как в энергетике встречаются в основном случайные процессы, т. е. случайные функции времени.

1-2. СЛУЧАЙНЫЕ СОБЫТИЯ

В энергетике случайные события имеют место, так же как и всех других отраслях деятельности человека. Энергетические системы объединяют большое число различных технических устройств: генерирующих, передающих или преобразующих энергию. Естественно, что условия работы большой совокупности даже однородных технических устройств резко отличаются друг от друга и носят с точки зрения энергетической системы как целого случайный характер. Так, например, то или иное устройство потребителей (электродвигатель, электровоз, электрическая лампа, электронагревательный прибор) случайно может быть или включенным, или отключенным

от электрической сети, работать с той или иной степенью использования. В результате наложения друг на друга таких случайных событий получается, например, та или иная величина спроса электрической мощности в энергосистеме, зависящая от совокупности случайных событий. Аварийные повреждения отдельных элементов энергетической системы(котлов, турбогенераторов трансформаторов, линий передачи) или снижения располагаемой мощности (из-за заноса поверхностей нагрева котлов, проточной части турбин и т. п.) также являются случайными coбытиями, возникающими в результате наложения большого числа неблагоприятных условий. Аварийные повреждения оборудования могут вызвать при отсутствии достаточного резерва мощности генерирующих источников необходимость перерывов в электроснабжении

части потребительских установок. Таким образом, основные условия работы

энергосистемы. а именно условия, определяющие величины суммар­ного спроса мощности в энергосистеме и суммарной располагаемой мощности для его покрытия, в свою очередь, определяются боль­шим числом случайных событий. Только зная вероятностные харак­теристики таких случайных событий, можно правильно определить суммарную величину спроса, величину необходимого резерва мощ­ности и т. д.

В энергетике очень важно при решении задач оптимизации, т. е. выборе оптимальных решений, использовать вероятностные харак­теристики случайных явлений. Например, надежность электро­снабжения отдельных потребителей зависит от случайных событий. Она определяется аварийными повреждениями оборудования, через которое потребитель получает питание электрической энергией. Можно выбрать схему питания потребителя или более надежной (наличие резервного питания), или менее надежной (однократное питание). Очевидно, что оптимальная схема будет соответствовать минимуму затрат. Чтобы найти этот минимум, следует оценить не только затраты на создание той или иной схемы элект­роснабжения, но и вероятный ущерб от перерывов электроснабже­ния для каждой из рассматриваемых схем. Определение вероятного ущерба невозможно без использования методов теории вероятностей.

Возможны два метода определения вероятности случай­ного события: классическое и статистическое.

Классическое определение, или подсчет вероят­ности, применимо только в том случае, если изучаемые случайные события образуют так называемую полную группу попарно несовместимых и равновозможных событий. События, образующие такую группу, называются случаями. Это означает, что одно событие из совокупности случайных событий должно произойти обя­зательно, т. е. возникновение хотя бы одного из событий досто­верно. Кроме того, два события из этой группы одновременно воз­никнуть не могут и любое из событий данной группы имеет оди­наковую вероятность. В этом случае вероятность считают равной отношению числа случаев, когда данное событие происходит, к об­щему числу возможных случаев. Как видно из данного определения, понятие классического определения вероятности может применяться редко, так как обычно на практике общее число случаев, а также число «благоприятных» случаев, когда данное событие происходит, не может быть подсчитано. Кроме того, допущение о равной воз­можности тех или иных событий данной группы не всегда удается доказать. Поэтому в энергетике, например, приходится пользоваться только статистическим определением вероятности.

Статистическое определение вероятности, как по­казывает само название, базируется па статистических материалах. Наблюдая какое-либо случайное событие или осуществляя соответ­ствующие испытания, можно определить относительную частоту воз­никновения данного события. При достаточно большом числе наблю­дений или испытаний относительная частота возникновения события колеблется около некоторой постоянной величины, называемой статистической вероятностью данного случайного события. Ее можно определить достаточно точно, если произвести большое число наблю­дений или испытаний. Таким образом, вероятность случайного собы­тия вскрывается только на основе статистических материалов. При отсутствии таких материалов, а также при малом числе испытаний или наблюдений определить статистическую вероятность случайного события даже приближенно не представляется возможным. Естественно, что математическая статистика, изучающая законы обработки статистических материалов, является разделом теории вероятностей. Отсюда следует упомянутое выше положение, что использовать аппа­рат теории вероятностей для решения каких-либо практических задач нельзя, не располагая необходимым исходным статистическим материалом достаточного объема.

Различные случайные события символически обозначаются боль­шими буквами А, В, С; достоверное событие обозначается буквой U, а невозможное событие—буквой V. ^

Рассмотрим различные связи случайных событий и их символическое изображение:

1) А∩В. Событие А содержится в В, т. е. если событие А происходит, то обязательно происходит и событие В;

2) А = В. Событие А происходит, если происходит В, и наоборот. Это условие эквивалентно двум условиям: А∩В и В ∩А;

3) АВ. События А и В происходят одновременно;

4) А+В. Происходит или событие А, или событие В, или оба одновременно (происходит хотя бы одно из событий А и В)',

5) А—В. Событие А происходит, но при этом событие В не происходит;

6) Ā — событие противоположное А. Если А происходит, то Ā не происходит, и наоборот. При этом A+A = U, τ. е. одно из событий А или Ā обязательно происходит. Кроме того, A·Ā=V, т. е одновременно А и Ā не могут происходить;

7) AB = V. События А и В несовместимы, т. е. одновременно произойти не могут. Отличие несовместимых событий от противоположных в том, что несовместимые события могут вообще не происходить; 8) А =В₁+В₂ = В₃ и В₁В₂ = В₁В₃ = В₂В₃ = V. Событие А подразделяется на частные случаи: В1,В₂ и В₃, которые попарно несовместимы. Событие A может не происходить вообще;

9) В₁+В₂+В₃ = U и В₁В₂= В₁В₃ = В₂В₃ = V. Полная группа несовместимых событий. Одно из них обязательно происходит (в от­личие от п. 8).

Наглядное графическое представление указанных связей между случайными событиями дает рис. 1-1, на котором всем рассмотрен­ным случаям соответствует квадрат с площадью, равной единице. На площадь этого квадрата произвольно ставится точка, что соот­ветствует некоторому конкретному случаю. Если точка попадает в область А, то событие А происходит. Если она попадает вне области А, то событие А не происходит (площадь области А характери­зует вероятность события А. Заштрихованная часть квадрата соот­ветствует событию.

В дальнейшем будем обозначать вероятность события А через Р(А}. (Вероятность рабочего состояния будет сокращенно обозначаться через р, а вероятность аварийного состояния—через q.)

Два случайных события, например А и В, будут считаться не­зависимыми, если наступление одного из них не влияет на вероят­ность наступления друго­го, и зависимыми— в об­ратном случае.

Обычно в энергетике приходится изучать веро­ятности не простых слу­чайных событий, а слож­ных случайных событий, являющихся комбинация­ми ряда простых (элемен­тарных). Определение ве­роятности сложного собы­тия через известные значе­ния вероятности простых событий производится ис­ходя из так называемых законов вероятности сложных событий. Для независимых случайных событий эти законы могут быть сформулированы следующим образом:

1) вероятность возникновения хотя бы одного из двух случай­ных независимых и несовместимых событий А и В равна сумме вероятностей этих событий. Возникновение одного из двух случай­ных событий А и В символически обозначается их суммой А + В;

Р(А + В) = Р(А) + Р(В); (1-1)

2} вероятность возникновения хотя бы одного из двух незави­симых и совместимых случайных событий А и В может быть записа­на как

(1-2)

3) вероятность' одновременного возникновения двух несовмести­мых событий А и В равна нулю. Одновременное возникновение двух событии А и В символически обозначается их произведением АВ. В данном случае

Р(АВ) = 0;. (1-3)

Рис. 1-1

4) вероятность одновременного возникновения двух независимых и совместимых событий равна произведению их вероятностей:

Р(АВ) = Р{А)Р(В}; (1-4)

5) сумма вероятностей противоположных событий равна единице, Событие Ā, противоположное данному событию А, всегда происхо­дит, если не происходит событие А, и всегда не происходит, если событие А происходит, т. е.

Р(Ā)+Р(А) = 1. (1-5)

Вероятность противоположного события

Р(А)=1 -- Р{А). (1.6)

Рассмотрим применение указанных законов в энергетике.

Ава­рийные повреждения оборудования являются случайными событиями. При большом числе агрегатов электростанций и элементов сети повреждение одних устройств может сочетаться с повреждением других устройств. Возникает задача определения вероятности одно­временного повреждения двух, трех и более устройств (агрегатов) или элементов сети. В ряде случаев необходимо также определять вероятность того, что никаких повреждений в энергосистеме нет, так как эта величина характеризует надежность работы всего обо­рудования. Эти задачи возникают обычно при необходимости выбора оптимального решения, связанного с обеспечением или надежности работы энергосистемы (выбор оптимального резерва мощности), или надежности питания отдельных потребителей (выбор оптимальной схемы электроснабжения потребителя), или устойчивости энерго­системы (выбор оптимального уровня устойчивости). Во всех этих случаях отдельные повреждения рассматриваются как независимые и совместимые случайные события. Вероятность каждого из них может быть определена как статистическая вероятность на основе длительного наблюдения над аварийностью данного или однотипного оборудования. Для иллюстрации определения вероятности сложных событий рассмотрим примеры.

Пример 1-1. Определить вероятность повреждения энергетического блока, представляющего coбoй последовательное соединение парового котла с паровой турбиной и электрическим генератором. Паровая турбина получает весь пар от парового котла. Генератор расположен на одном валу с турбиной, т. е. исполь­зует всю ее мощность. Вероятности повреждения отдельных элементов блока известны: для q_k = 0,02; q_т = 0,01; q_г для котла, турбины и генератора соот­ветственно.

Очевидно, что аварийный выход из работы всего блока может иметь место при повреждении хотя бы одного из трех указанных элементов блока. Так как неповреждение является случайным событием, противоположным повреждению, то вероятности неповреждения элементов блока [см. (1-6)]

р_к = 1 --0,02=0,98; р_т= 1—0,01=0,99; р_г = 1 --0,001 = 0,999.

Найдем вероятность того, что все элементы блока не повреждены, т. е. блок работает исправно. Так как аварийность каждого элемента можно считать неза­висимой от других элементов, то вероятность того, что все три элемента не по­вреждены, т. е. вероятность работы блока |см. (1-4)

р_бл = р_кр_т р _г = 0,98-0,99.0,999= 0,9692298.

Повреждение блока по любой причине является событием, противоположным по отношению к неповреждению блока, поэтому вероятность повреждения блока

q_бл = 1 — 0,9692298 = 0,0307702.

Можно определить эту же величину, если рассмотреть все частные случаи

(их может быть только семь) повреждения элементов блока: а) котла; б) турби­ны; в) генератора; г) котла и турбины; д) котла и генератора; с) турбины и ге­нератора; ж) котла, турбины и генератора.

Найдем вероятность каждого из этих частных случаев повреждения блока, исходя из формул (1-4) и (1-6):

а) вероятность повреждения котла,

0,02·0,99-0,999= 0,0197802.

Было бы неправильным считать, что вероятность повреждения только котла равно 0,02, так как в число событий «повреждение котла» вошли бы события одновременного повреждения котла и других элементов,

В случае а) интерес представляет повреждение только котла при неповреж­дении других элементов. Именно поэтому 0,02 умножается на 0,99 и 0,999;

б) вероятность повреждения турбины

0,98-0,01.0,999=0,0097902.

Аналогично получим вероятности для остальных случаев:

в)0,98.0,99.0,001 =0,0009702;

г) 0,02.0,01.0,999 = 0,0001998;

д) 0.02.0,99.0,001 = 0.0000198;

е) 0,98.0,01.0.001=0.0000098;

ж) 0,02.0.01.0,001 =0,0000002.

Если сложить вероятности для всех семи случаев, то получится вероятность повреждения блока, равная 0.0307702. Как видно, для определения вероятности повреждения блока первый путь гораздо проще и требует меньше расчетов. Зато второй путь позволяет не только получить величину общей вероятности повреж­дения блока, но и проанализировать вероятность различных причин повреждения всего блока. Наибольшее значение имеет вероятность повреждения котла, а за­тем—турбины. Вероятность этих двух случаев составляет 0,0295704 из общей вероятности 0,0307702.

Пример 1-2. Потребитель питается по двухцепной линии электропередачи. Вероятность повреждения и выхода из строя каждой цепи составляет q = 0.001. По любой из цепей потребитель может получить всю нужную ему мощность. Ка­кова вероятность сохранения электроснабжения данного потребителя?

Потребитель теряет электроснабжение только в случае аварийного выхода обеих цепей. Вероятность этого но (1-4) равна 0,001.0,001 = 0,000001. Вероят­ность сохранения питания, т. е. надежность энергоснабжения, по (1-6) равна 1—0,000001= 0,999999.Если по одной цепи может быть передано только 50% мощ­ности, то вероятностъ передачи только 50% мощности можно определить так. Вероятность выпадения первой цепи при сохранении второй равна 0,001.0,999 = 0.000999, где второй множитель соответствует вероятности сохранения второй цепи. Вероятность выпадения второй цепи при сохранении первой составляет 0,999.0.001 = 0,000999. Суммарная вероятность.выпадения только одной цепи по (1.1) определится как сумма обеих вероятностей, т. е. 0,001998. Вероятность сохранения полной нагрузки, очевидно, равна 0,999·0.999 = ·0,998001, а вероятность полной потери питания равна 0.001.0,001 = 0,000001. Заметим, что сумма вероятностей сохранения полной наг рузки, сохранения 50% нагрузки и полной потери питания равна единице, так как эти события составляют полную группу несовместимых событий;

0,998001+0,001998+0,000001=1.

Рассмотрим вероятности зависимых__случайных событий. Пусть события А и В являются зависимыми,т.е. вероятность одного из этих событий изменяется, если происходит другое событие. Для оценки этого вводится понятие условной вероятности.

Условной вероятностью события А по В называется вероятность события А, если происходит событие В. Она обозначается через Р{А/В}.

Основные законы для взаимозависимых случайных событий фор­мулируются следующим образом:

1) условная вероятность события А по В при их совместимости и взаимозависимости равна отношению вероятности одновременного наступления событий А и В к вероятности события В:

Р{А/В}==Р(АВ)/Р(В}, (1-7)

причем Р(АВ) в этом случае не равно Ρ (Α}· Ρ {В};

2) вероятность одновременного наступления двух взаимозависимых и совместимых событий, как это следует из (1-7), равна произ­ведению условной вероятности первого события по второму на ве­роятность второго события:

Ρ (АВ) = Ρ (А/В) Ρ (В). (1-8)

Взаимозависимыми событиями в энергетике являются, например,

повреждения отдельных фаз линии передачи. При повреждении одной фазы линии передачи в сети с незаземленной нейтралью на­пряжения других фаз возрастают в √3 раз, что увеличивает веро­ятность повреждения других фаз. Но даже в сети с заземленной нейтралью, где повышение напряжения на других фазах не проис­ходит, ионизация воздуха, обусловленная коротким замыканием на одной фазе, способствует перекрытию других фаз. Если исходное повреждение одной фазы является независимым случайным собы­тием, то одновременное повреждение фаз в том же месте является зависимым случайным событием.

Пример 1-3. Пусть статистическая вероятность повреждения любой фазы линии составляет 0,001. Примем также, что если повреждение одной фазы про­изошло. го повреждение любой другой фазы будет иметь статистическую вероятность 0.2, т. е. условная вероятность повреждения второй фазы при повреждении первой равна 0,2. Кроме того, пусть аналогичные вероятности повреждения третьей фазы при повреждении двух других составляют 0,5. Определим соотношения вероятностей одно-, двух- и трехфазных коротких замыканий при условии, что авария началась с повреждения одной фазы.

Вероятность аварийного повреждения двух фаз [см. (1-8)] p’=0,2.0,001 =0,0002.

Вероятность аварийного повреждения трех фаз р"==0,5·0,0002=0,0001.

Определим условные вероятности развития аварии, т. е. условные вероят­ности повреждения других фаз. Пусть статистические наблюдения установили, что однофазных коротких замыканий в данной сети за некоторый длительный период времени было 100, а в 20 случаях из них повредилась и другая фаза. Тогда на основании формулы (1-7) можно получить условную вероятность по­вреждения и другой фазы;

Р(А/5)==Р(АВ)/Р(В)=20/100==0,2,

так как число аварий можно считать пропорциональным вероятности.

Таким образом, соотношения вероятностей одно-, двух- и трехфазных повреж­дений будут: 0,001; 0,0002; 0,0001 или примерно 77% однофазных, 15% двух­фазных и 8% трехфазных.

При большом числе однотипных агрегатов в электрической системе вероятности повреждения различного числа агрегатов могут быть определены по биноминальной формуле вероятности для схемы не­зависимых испытаний (схема Бернулли).

Во многих практических случаях при многократных независимых испытаниях могут быть только два исхода: случайное событие А произойдет или не произойдет. Пусть вероятность того, что в каж­дом из этих независимых испытаний событие А произойдет, равна р, где р— статистическая вероятность. Тогда вероятность противопо­ложного события (событие А не происходит)

q = 1 – p.

Зная р или q, можно определить вероятность того, что в n не­зависимых испытаниях событие А, например повреждение агрегата, случится m раз. Обозначим эту вероятность через Р^m_n. Она_равна, произведению числа комбинаций из n по т на вероятность события в степени т и на противоположную вероятность в степени {п—т):

(1-9)

Выражение (1-9) называют формулой биноми­нального распределения. Очевидно, что

(1-10)

так как эта сумма охватывает все возможные события (т варьиру­ется от 0 до n).

Формулу (1-9) можно получить также, рассуждая следующим образом. Рассмотрим выражение (q + p)^m Оно, очевидно, равно еди­нице, так как (q +p) = 1. Разлагая п-ю степень бинома (q+р) в ряд по известному закону, получим

(1-11)

Нетрудно понять смысл членов разложения. Первый член qⁿ соответствует вероятности того, что в n испытаниях событие А не произойдет ни разу, т. е. равен Р⁰; второй член—вероятности того, что в n испытаниях событие А произойдет только один раз; т. е. равен P¹_n. Действительно, вероятность того, что событие произойдет при каком-то одном определенном испытании, будет pq ^n--1, а веро­ятность того, что событие произойдет при каком-то любом одном испытании, в n раз больше и т. п. Член разложения (m+1)-й, соответствующий вероятности того, что событие происходит т раз, равен C^m_n q^n-m p^m, т.е. Р^m_n [см. (1-9)].

Вместо различных испытаний рассмотрим различные однотипные агрегаты, предполагая, что вероятность аварийного состояния для каждого из агрегатов одинакова и равна q.

Пример 1-4. Пусть р, энергосистеме имеется группа из п однотипных агрега­тов (например, котлов или турбин), находящихся в совершенно одинаковых ус­ловиях; вероятность исправного состояния агрегата равна р, а вероятность

противоположного события, т. е. неисправного состояния агрегата (аварийного ре­монта), равна q. Найдем вероятность рабочего состояния m агрегатов из числа n,

причем т изменяется от 0 до п·

Нетрудно убедиться в том. что разложение по (1-11) определяет искомый ряд вероятностей. В самом деле, qⁿ—это. очевидно, вероятность того, что все агре­гаты повреждены и число работоспособных агрегатов равно нулю; npq^n--1—ве­роятность того, что только один агрегат находится в рабочем состоянии;

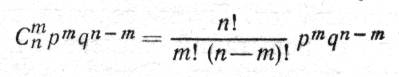
— вероятность рабочего состояния т агрегатов; pⁿ— вероятность того, что все агрегаты находятся в исправном.и состоянии.

Если определять вероятность не рабочего состояния, а аварийного повреж­дения различного числа агрегатов, то целесообразно записать тот же ряд в сле­дующем порядке:

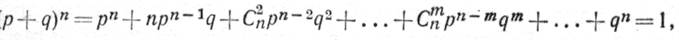
(1-11а)

где(m + 1)·й член определяет вероятность выхода из работы т агрегатов, рав­ную

C^m_n p^{n – m} q^m.

Если, например, п=5, р==0,98 и q=0,02, то вероятность отсутствия ава­рийных выходов

рⁿ = 0,98⁵ = 0,905. Вероятность аварии с одним агрегатом

и т. д.

Пример 3-5. Определим вероятность выхода из строя какого-либо количества агрегатов в -энергосистеме. Если в системе имеется пять групп однотипных агре­гатов с числом агрегатов n₁ – n₅ и вероятностями повреждения агрегатов q₁ – q_5, тο вероятности любых комбинаций одновременных повреждении агрегатов можно найти из разложения выражения

Так, например, вероятность аварийного выхода двух агрегатов 1-й группы, одного агрегата 3-й группы и одного агрегата 5-й группы равна

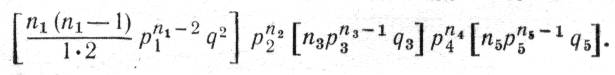
1-3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

К случайным величинам в энергетике относятся такие важные

параметры режима, атокак спрос электрической мощности и энергии, отклонения частоты и напряжения в электрических сетях от номи­нальных значений, располагаемая мощность электростанций, мощ­ность агрегатов в аварийном ремонте, длительности безаварийной работы и аварийного ремонта отдельных агрегатов, напор на гидро­станциях и т. д. Знание закономерностей изменения этих случай­ных величин необходимо как при проектировании, так и при экс­плуатации энергетических систем. Основой для их изучения является статистический материал и методы теории вероятности.

Прежде чем рассматривать случайные величины в энергетике, остановимся на

методах описания их закономерностей. Случайные величины можно разделить на два класса: дискретные и непрерыв­ные. Дискретная случайная величина может принимать только дискретные значения, например число агрегатов, вы­шедших аварийно из работы. Это число в ограниченном интервале является конечным. Значения непрерывных случайных величин могут изменяться непрерывно, т. е. даже в ограниченных интервалах такие величины могут иметь бесконечно большое число значении, напри­мер -- ошибка прогнозирования суммарного спроса мощности. Для дискретных случайных величин распределение вероятностей различ­ных их значений может быть наиболее просто задано с помощью таблиц распределения, в которых в верхней строке указываются все значения, принимаемые данной дискретной случайной величиной, а в нижней — вероятности соответствующих ей значений. Очевидно, что сумма вероятностей должна равняться единице, если данная случайная величина всегда принимает одно из возможных значений.

Пример 3-6. В энсргетической системе, в ключающей четыре однотипных гене­ратора, требуется найти вероятности одновременною выхода из строя нескольких генераторов

Вероятность аварийного выхода каждого q=0,02, вероятность рабочего со­стояния p = 0.98. Случайной величиной будем считать число агрегнтов т, вышед­ших в аварию. Эта величина является дискретной и может принимать значения О, 1. 2. 3, 4.

Пользуясь формулой биноминального распределения, можно найти вероят­ность выхода из работы агрегатов

Р^m_n = C^m_n p^{n – m} q^m.

Сделав подсчет по этой формуле, получим таблицу распределения вероятнос­тей cлучайной величины—числа аварийных агрегатов:

Число аварийных

агрегатов т... 0 1 2 3 4

Вероятность... 0,92237 0,07530 0,00230 0,00003 0,00000

Сумма вероятностей равна единице.

Закон распределения вероятностей непрерывных случайных ве­личин нельзя представить в виде таблицы, так как число значений таких случайных величин бесконечно даже в ограниченном интер­вале. Кроме того, вероятность получить какое-либо определенное значение равна нулю. На первый взгляд это парадоксально. Если задана непрерывная случайная величина в некотором ограниченном интервале, а вероятность любого значения ее в этом интервале равна нулю, то вообще такая величина как будто бы не может иметь ни­какого значения во всем данном интервале. Ведь вероятность, рав­ная нулю, является вероятностью невозможного события. Однако парадокса здесь нет, и если говорить точнее, то вероятность того, что какая-либо непрерывная случайная величина имеет какое-то определенное значение, бесконечна мала. Вспомним классическое определение вероятности как отношение числа случаев, при которых происходит событие М, к общему числу случаев N. Событием будем считать принятие случайной величиной опреде­ленного значения. Тогда Μ = 1, но общее чиcло таких случаев даже в ограниченном интервале равно бесконечности, так как бесконечно велико число возможных значений. Поэтому N = --∞. Вероятность принятия случайной ветчиной определенного значения по формуле

классической вероятности 1/∞ = 0, т.е. бесконечно мала. В данном случае нулевое значение вероятности попадания в определенную точку связано не с невозможностью самого события (отсутствие случаев, когда оно может произойти), а с бесконечно большим числом возможных случаев. Поэтому для непрерывных случайных величин определяют вероятности попадания не в точку, а в неко­торый интервал. Этот интервал, однако, можно принять сколь угодно малым. Следует напомнить, что точно измерить какую-либо вели­чину практически нельзя, поэтому измерение проводят в некотором интервале.

Для количественной оценки вероятностей как непрерывных, так и дискретных случайных величин вводят функцию распределения F {х), которая, по определению, равна вероятности того, что данная слу­чайная величина η (непрерывная или дискретная) попадает в ин­тервал значений от — ∞ до некоторого значения х, т. е. она меньше, чем х:

F(x)=P( -- ∞ ≤ η< x). (1-12)

Из определения следует, что F(— ∞)=0 и F(+ ∞) =1. Чтобы найти функции распределения дискретной случайной ве­личины, можно использовать таблицы распределения, производя суммирование вероятноcтей слева направо. Для примера (1-6)

F(0) = 0; F (Ί) = 0,92237; F(2) = 0,99767; F(З) = 0,99997; F(4) = 1.

Для непрерывных случайных величин функция распределения задается аналитически, если это возможно, или графически. По за­данной функции распределения можно вычислить вероятности попа­дания случайной величины в определенный интервал значений (x₁. x₂₎ Если известны значения F(х₁) и F (х_{2 )} для случайной величины η, то искомая вероятность попадания в интервал

P(x₁ ≤ η< x₂) = F(x₁) – F(x₂), (1-13)

т. е. для того, чтобы определить вероятность попадания непрерыв­ной случайной величины η в интервал (x₁, x₂). где x₁ < x₂ доста­точно взять разность функций распределения при значениях x₁ и x².

Закон распределения вероятностей непрерывных случайных ве­личин может быть определен заданием не функции распределения, а плотности распределения вероятностей φ(x), которая представляет собой производную от функции распределения по значению слу­чайной величины х :

φ (x) = dF (x) / dx. (1-14)

Следовательно,

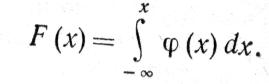(1 – 15)

}ах.

Плотность распределения вероятностей, очевидно, есть предел, к которому стремится отношение пероягносгн попадания в интервал к величине интервала при неограниченном приближении верхней границы интервала к нижней.

Если плотность распределения вероятностей задана аналити-

чески, то вероятность попадания непрерывной случайной величины в какой-либо интервал (x₁, x₂), где x₁ < x₂,

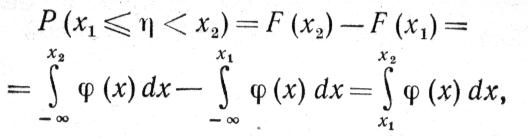(1 -16)

т.е. равна интегралу от плотности распределения вероятностей,взятому в пределах искомого интервала.

В энергетике широко применяют случайные величины со следующими распределениями вероятностей: равномерное, простейшее нормальное, общее нормальное, биноминальное, по закону Пуас­сона. В литературе для них даны формулы функций и плотности распределения вероятностей, а также формулы, определяющие вероятность попадания случайной величины в заданный интервал. Нормальное распределение, как простейшее, так и общее, используют при нахождении вероятностей ошибок прогнозирования на­грузки потребителей энергосистемы, отклонения нагрузки энерго­системы и отдельных ее узлов от средних значений, и т. п. Бино­минальное распределение и распределение по закону Пуассона при­меняют при определении вероятностей различных значений аварий­ных снижений мощности в энергосистеме и аварийного выхода раз­личного числа агрегатов в группе однотипных и т. д. Равномерное распределение служит основой метода статистических испытаний (метод Монте-Карло), применяющегося при определении резерва мощ­ности, отказа в срабатывании автоматики и т. п.

Из-за отсутствия соответствующих статистических материалов не всегда можно задать таблицы распределения вероятностей для дискретных случайных величин или функции распределения и плот­ности распределения вероятностей для непрерывных случайных ве­личин. Однако и не для всех практических задач требуется знать полные вероятностные характеристики случайной величины. Во мно­гих случаях достаточно знать основные числовые характеристики случайных величин, к числу которых относятся математическое ожидание, дисперсия, стандартное отклонение и моменты случайной ве­личины.

Случайная величина может приобретать различные значения, поэтому важно знать ее среднее значение. Однако, если известна совокупность значений случайной величины, то простое среднее значение, определяемое как сумма возможных значений, разделен­ная на их число, еще не характеризует действительных условий. Ведь различные значения случайной величины могут иметь различ­ные вероятности, и поэтому более вероятные значения будут чаще встречаться на практике и в большей мере определять истинное среднее значение случайной величины. Поэтому для оценки среднего (в вероятностном смысле) значения случайной величины вводится понятие математического ожидания, предъявляющего собой дейст­вительно среднее значение случайной величины, определяемое с учетом различных вероятностей отдельных значений. Математическое ожидание (в дальнейшем сокращенно м. о.) случайной величины η или α будем обозначать как М(η) или М(α).

Определим м. о. для случайной дискретной величины. Пусть заданы вероятности различных значений случайной дискретной ве­личины:

Значение η x₁ x₂ x₃

Вероятность p₁ p₂ p₃

Примем, что общее число испытаний составляет n, причем m₁ раз получалась величина x₁, m₂ раз и т. д. Тогда м. о., пред­ставляющее собой действительное среднее значение случайной ве­личины,

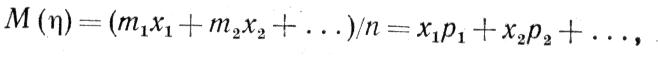
(1 -1 7),

так как вероятности р₁ = m₁ / n, р₂= m₂/ n₁ и т. д.

Таким образом, для дискретной случайной величины

, (1-18)

причем суммирование происходит по всем значениям дискретной величины x_к имеющим вероятности p_к. Аналогично для непрерывной случайной величины

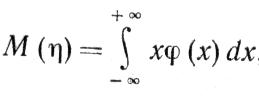(1-19) где φ (x) — плотность вероятности.

Пример 3-7. Пусгь в энергосистеме возможны дефициты мощности 5О. 100 и 150 МВт, причем вероятноетн этих дефицитов соответственно равны 0.001; 0,0004; 0,0002.

Требуется определить м. о. недоотпуска энергии за год.

При постоянном дефиците,5Ο МВт недоотпуск анергии за год составил бы 50.8760 МВт.ч, при дефиците 100 МВт—100·87бО МВт.ч и т. д. -Поэтому м. о. недоотпуска

Μ (η)=50·8760·0,001 + 100.8760.0.0004+ 150-8760.0.0002 = 1051 МВт.ч.

В теории вероятностей доказывается ряд теорем, связанных с м. о., которые здесь приводятся без доказательств:

1) м. о. постоянной величины С равно этой величине, т. е М{С}=С, так как вероятность постоянной величины равна единице;

2) м. о. произведения случайной величины на постоянную С равно произведению постоянной величины С на м. о. случайной ве­личины:

М(Сα) = СМ (α) (1.20)

3) м. о. суммы случайных величин равно сумме м. о. каждой из величин в отдельности:

M(α+β)=Μ(α)+ M(β) (1-21)

4) м. о. произведения независимых случайных величин равно произведению м. о. каждой из величин:

M(αβ) = M(α) M(β) (1.22)

Статистическое среднее, т. е. м. о. случайной величины, харак­теризует действительное среднее значение случайной величины, однако этого недостаточно для ее полной характеристики. Необхо­димо знать, насколько отклоняется случайная величина от своего м.о. Если эти отклонения невелики, то м. о. достаточно хорошо представляет случайную величину; если же отклонения велики, т. е. разброс значений случайной величины или их рассеяние велико, то одно м. о. уже не характеризует данную величину. Нельзя определять степень отклонения случайной величины от ее м. о. по среднему значению отклонения случайной величины от ее м. о., так как эта величина всегда равна нулю. Действительно,

М [ α – M(α)] = M (α) – M (α) = 0

так как функция M (α) постоянна. Это объясняется тем, что м. о. является как бы центром всех значений случайной величины, и от­клонения одного знака компенсируют отклонения другого знака. Поэтому в качестве меры отклонений cлучайной величины от ее м.о. принимают величину, равную м. о. квадрата отклонения слу­чайной величины от ее м. о., которую называют дисперсией случай­ной величины α и обозначают через D (α);

D (α) = M [α -- M (α) ] ² (1-23)

Квадратный корень из величины дисперсии называется средне­квадратичным или стандартным отклонением случайной величины:

_____

δ (α) = √D(α) (1-24)

Для дискретных случайных величин

D(α) = ∑[x_к -- M(x)]², (1-25)

где суммирование распространяется на все значения случайной ве­личины x_k,имеющие соответствующие вероятности p_k.

Для непрерывной случайной величины

(1-26)

(3-)

В теории вероятностей доказывается ряд теорем о дисперсии случайных величин, которые здесь приводятся без доказательств. 1.Дисперсия постоянной величины С равна нулю:

D(C) = 0. (1-27)

  -

2. Дисперсия произведения постоянной величины С на случайную величину α равна произведению квадрата постоянной вы С на дисперсию случайной величины

D(Cα) = C² D (α). (1-28)

3. Дисперсия суммы постоянной С и случайной α величин равна дисперсии случайной величины:

D (C + α) = D(α) (1-29)

4. Дисперсия суммы независимых случайных величин α и β равна сумме дисперсий этих величин:

D(α + β) = D(α) + D(β).

5. Дисперсия среднеарифметического от ряда n случайных величин с одинаковой дисперсией в n раз меньше дисперсии каждой из этих величин в отдельности:

D[(α₁ + α₂ + ……+ α_n)/ n ] = 1/n² [D(α₁) + D (α₂) +…. ] = D(α_i) / n

(1-31)

Пример3-8. Пусть среднемесячная максимальная нагрузка энергосистемы равна 1200МВт, Примем, что отклонения суточных максимумов в рабочие дни данного месяца подчинены закону нормального распределения с известными числовыми характеристиками. Найти вероятнсть того. что суточный максимум будет колебаться и пределах 1250... I300 МВт или 1050…. 1120 МВт. При этом задано, что дисперсия D(η) = 2500. а стандартное отклонение δ (η) = 50.

Воспользуемся выражением для вероятности попадания случайной (нормаль­ного распределения) величины в заданный интервал.

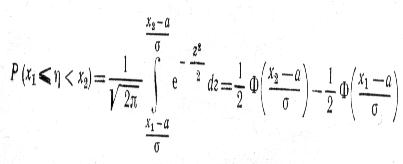
где Φ (х)— это интеграл вероятностей.

Математическое ожидание равно 1200, т.е. а = 1200. Тогда, учитывая, что σ = δ(η) = 50, найдем искомые вероятности суточного максимума:

Ρ(1250≤η< 1300) = 0,5Ф [(1300 – 1200)/ 50] – 0,5[(1250 –1200) /50 ] =

=0,5Ф(2)—0,5Ф(1) = 0,47725—0,34134=0,1359;

Ρ(1050 ≤ η < 1120)=0,5Ф[(1120–1200) / 50 ] – 0,5Фх [(1050 –1200) / 50] =

=0,5Ф(--1,6) -- 0,5Ф(-3) = -- 0,5Ф (1,6) + 0,5Ф (3) -- 0,44520+0,49865= =0,05345.

Дата добавления: 2014-01-07