Распределение вероятностей

Из предыдущего раздела следует, что при обработке результатов измерений для оценки погрешностей измерений, важную роль играют функции распределения вероятностей. На практике могут реализовываться различные распределения вероятностей, поскольку кроме разброса измеряемых значений из-за случайных ошибок существуют статистические флуктуации самой измеряемой величины. В качестве примера можно привести радиоактивный распад, который является случайным процессом по своей природе.

В лабораторном практикуме для нас будут играть важную роль два распределения вероятностей: нормальное распределение (распределение Гаусса) и равномерное распределение.

Нормальное распределение (распределение Гаусса)

Важная роль гауссова распределения объясняется тем, что, с одной стороны, оно хорошо описывает плотность вероятностей для многих физических величин, а с другой – распределение численных значений при самых разных измерениях. Кроме того, многие другие распределения переходят в предельном случае в нормальное распределение. Поэтому их можно заменить распределением Гаусса.

Плотность вероятностей в распределении Гаусса для случайной переменной х имеет вид

(3.1.1)

где х ₀ – математическое ожидание случайной величины (истинное значение измеряемой величины при отсутствии систематических погрешностей), σ ² – дисперсия случайной величины; 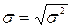- среднеквадратичное отклонение (стандарт) распределения.

Среднеквадратичное отклонение σ непосредственно характеризует ширину распределения вероятностей, те. разброс измеряемых значений.

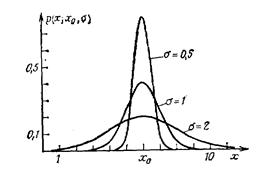На рис 3.2. показано нормальное распределение со значениями параметра σ = 0,5; 1 и 2. Оно характеризуется следующими особенностями:

1. Распределение симметрично относительно точки х = х ₀.

2. Математическое ожидание (среднее значение) вычисляется как

Рис.3.2. Плотности вероятностей для нормального распределения при значениях параметра σ = 0,5; 1; 2.

(3.1.2)

Ему соответствует максимальная плотность вероятностей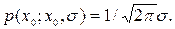

3. По обе стороны от максимума величина р монотонно падает и асимптотически стремится к нулю.

4. Дисперсия и среднеквадратичное отклонение определяются как

Дисперсия = (3.1.3)

среднеквадратичное отклонение (стандарт) =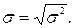

5. На рис. 3.2 показано, что при увеличении среднеквадратичного отклонения распределение становится шире, а максимальное значение уменьшается. Вследствие условия нормировки 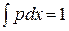площадь под кривой остается постоянной.

Решая уравнение (3.1.3) с учетом (3.1.2), получим

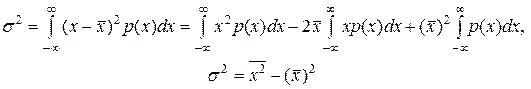(3.1.4)

Это выражение справедливо для всех распределений вероятностей и имеет большое практическое значение.

Совокупность всех возможных исходов измерения в данных условиях называют в математической статистике генеральной совокупностью. В нашем случае эта совокупность бесконечно велика (бесконечное число измерений), и поэтому теоретическое распределение вероятностей никогда не реализуется. Мы всегда имеем дело с конечным числом n измерений, которые называют выборкой объемом n. Эти значения представляют собой случайную выборку величин из генеральной совокупности. По результатам выборки мы должны как можно точнее узнать характеристики генеральной совокупности. Поэтому нужно определить соответствующие величины выборки, причем следует постоянно помнить, что величины в выборке случайным образом «извлечены» из генеральной совокупности. Поэтому, когда студенты (вне одного маршрута) приносят одинаковые данные – это говорит (мягко говоря) об их недобросовестности.

Наилучшим приближением истинной величины 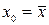является так называемое выборочное среднее значение

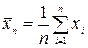, (3.1.5)

т.е. при конечном значении n, 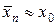, но 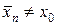. Этот факт мы обоснуем непосредственно при расчете погрешностей.

По аналогии с выражением (3.1.3) можно ввести выборочную дисперсию , которая определяется, как среднее значение квадрата отклонений 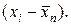Здесь не идет речь об истинной ошибке, поскольку не известно истинное значение .

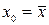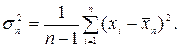
(3.1.6)

В этой формуле вместо 1/ n появляется множитель 1/(n -1), поскольку для расчета разностей 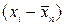нужно иметь, по меньшей мере, два результата. С математической точки зрения это означает, что только с учетом этого множителя выборочная дисперсия будет равна в пределе дисперсии генеральной совокупности.

Корень квадратный из выборочной дисперсии называют выборочным стандартным отклонение σ_n. Оно характеризует разброс отдельных результатов измерений вблизи среднего значения и является наилучшей оценкой среднеквадратичного отклонения σ генеральной совокупности, которое можно определить по выборке из n результатов.

Кроме среднего значения результатов измерений экспериментатора интересует еще и его точность. Мы можем определить ее, несколько раз повторяя серии по n измерений. Тогда величины математических ожиданий (выборочных средних значений) 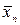образуют распределение, стандартное отклонение которого 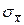будет характеризовать разброс средних значений 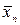от выборки к выборке. Поэтому величину 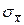называют стандартным отклонением выборочного среднего (или его средней ошибкой). Пользуясь законом сложения ошибок, получим

. (3.1.7)

Стандартное отклонение среднего, полученного по n измерениям, отличается в 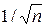раз от стандартного отклонения отдельного измерения. Таким образом, точность измерений достаточно медленно растет с увеличением количества измерений при больших n. Поэтому нужно стремиться не к увеличению количества опытов, а к улучшению измерительных методов, которые позволяют уменьшить стандартные отклонения 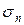отдельного измерения.

Статистическая достоверность (доверительная вероятность)

Вероятность того, что случайная переменная х, распределенная по нормальному закону, попадет в интервал [ x ₁, x ₂], равна (3.3)

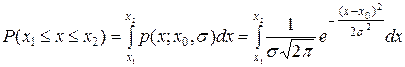. (3.1.8)

Этот интеграл нельзя представить в виде элементарных функций, и поэтому он табулирован в стандартизированном (нормированном) виде и представлен в математических приложениях в виде интеграла ошибок Гаусса erf(u).

Величину Р, иногда выраженную в процентах, называют также статистической достоверностью или доверительной вероятностью (надежностью) α (т. е. Р = α).

На рис. 3.3 показаны области ±σ и ±2σ для нормального распределения.

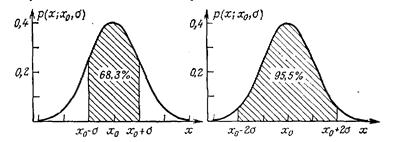
Рис. 3.3. Интервалы х₀ – σ ≤ х ≤ х₀ + σ и х₀ – 2 σ ≤ х ≤ х₀ + 2 σ.

Таблица 3.1

Интервал Р (или α), %

х₀ – σ ≤ х ≤ х₀ + σ 68,3 х₀ – 1,96 σ ≤ х ≤ х₀ + 1,96 σ 95 х₀ – 2 σ ≤ х ≤ х₀ + 2 σ 95,5 х₀ – 2,58 σ ≤ х ≤ х₀ + 2,58 σ 99 х₀ – 3 σ ≤ х ≤ х₀ + 3 σ 99,7

В таблице 3.1 приведены значения доверительной вероятности для нескольких практически важных интервалов.

Дата добавления: 2014-01-07