Полигональные сетки

Полигональные сетки представляют собой совокупность вершин, ребер и многоугольников. В качестве примера на рисунке 28 показана полигональная сетка, состоящая из шести вершин V₁…V₆, девяти ребер E₁…E₉, и четырех многоугольников P₁…P₄.

Сетку можно представить несколькими различными способами.

При явном задании многоугольников каждый многоугольник представляется в виде списка координат его вершин:

Вершины многоугольника запоминаются в том порядке, в котором они встречаются при обходе вокруг многоугольника. Все последовательные вершины многоугольника, а также первая и последняя вершины, соединяются ребрами.

Для описания сетки, показанной на рисунке необходимо описать четыре многоугольника.

P ₁ = ((x ₁, y ₁, z ₁), (x ₅, y ₅, z ₅), (x ₆, y ₆, z ₆)),

P ₂ = ((x ₁, y ₁, z ₁), (x ₂, y ₂, z ₂), (x ₅, y ₅, z ₅)),

P ₃ = ((x ₂, y ₂, z ₂), (x ₃, y ₃, z ₃), (x ₅, y ₅, z ₅)),

P ₄ = ((x ₃, y ₃, z ₃), (x ₄, y ₄, z ₄), (x ₅, y ₅, z ₅)),

Этот способ записи является эффективным для каждого отдельного многоугольника. Для полигональной сетки этот метод приводит к большим потерям памяти из-за дублирования информации о координатах общих вершин многоугольников, а также не дает явного описания общих ребер и вершин. Для поиска всех многоугольников, имеющих общую вершину, требуется сравнение троек координат одного многоугольника с тройками координат всех остальных многоугольников. Если же из-за ошибок округления одна и та же вершина в разных многоугольниках имеет разные координаты, то результат поиска может быть нулевой.

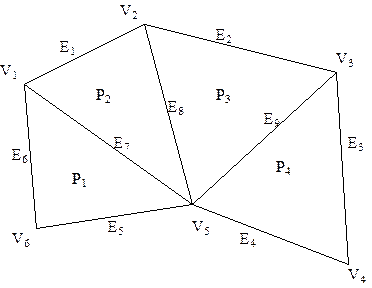
Рис. 28. Полигональная сетка.

При визуализации полигональной сетки общие ребра рисуются дважды – по одному разу для каждого многоугольника.

При задании многоугольников с помощью указателей в список вершин каждый узел полигональной сетки запоминается лишь один раз в списке вершин. Каждый многоугольник определяется списком указателей в список вершин. Так, для сетки показанной на рисунке XXX придется построить следующее описание.

V = (V₁(x ₁, y ₁, z ₁), V₂(x ₂, y ₂, z ₂), V₃(x ₃, y ₃, z ₃),

V₄(x ₄, y ₄, z ₄), V₅(x ₅, y ₅, z ₅), V₆(x ₆, y ₆, z ₆)),

P ₁ = (1,5,6), P ₂ = (1,2,5), P ₃ = (2,3,5), P ₄ = (3,4,5).

Этот метод требует меньшего объема памяти, легко изменить, например передвинуть любую вершину, но общие ребра многоугольников по-прежнему рисуются дважды.

При явном задании ребер многоугольников полигональная сетка задается в виде иерархической модели. Координаты каждого узла полигональной сетки запоминаются в списке вершин.

Создается список ребер, где каждое ребро указывает на две вершины в списке вершин. Каждый многоугольник задается как совокупность указателей на элементы списка ребер.

Полигональная сетка изображается вычерчиванием всех ребер (а не всех многоугольников).

Так, для сетки показанной на рисунке XXX придется построить следующее описание.

V = (V₁(x ₁, y ₁, z ₁), V₂(x ₂, y ₂, z ₂), V₃(x ₃, y ₃, z ₃),

V₄(x ₄, y ₄, z ₄), V₅(x ₅, y ₅, z ₅), V₆(x ₆, y ₆, z ₆));

E ₁ = (1, 2), E ₂ = (2, 3), E ₃ = (3, 4), E ₄ = (4, 5), E ₅ = (5, 6),

E ₆ = (6, 1), E ₇ = (1, 5), E ₈ = (2, 5), E ₉ = (3, 5);

P ₁ = (7,5,6), P ₂ = (8,7,1), P ₃ = (2,9,8), P ₄ = (3,4,9).

Заданную таким способом полигональную сетку наиболее просто проверять на непротиворечивость представления, т.е. на выполнение некоторых условий: что все многоугольники замкнуты, что все ребра используются по крайней мере один раз, но не более некоторого максимального числа раз, что на каждую вершину есть ссылка по крайней мере от двух ребер и т.п. Проверка непротиворечивости представления наиболее важна для полигональных сеток, созданных в интерактивном режиме (например, при оцифровке объектов), когда ошибки практически неизбежны.

Дата добавления: 2014-01-07