
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Матричная форма записи
Введем матрицу X размером n ´2 и вектор коэффициентов b размером 2´1, т.е.
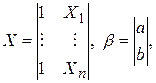
тогда e = y - Xb, а условия (6) записываются в виде X¢e = 0 или X¢ (y - Xb) = X¢y - X¢Xb = 0. Из последнего уравнения получаем
 (7)
(7)
где  . Представление (7) важно при изучении множественной регрессии.
. Представление (7) важно при изучении множественной регрессии.
Выше в рамках метода наименьших квадратов нас интересовали вопросы подгонки кривой. Далее определим ряд статистических свойств данных. Именно на этом этапе можно говорить о построении регрессионных кривых.
Запишем уравнение зависимости Yt от Xt в виде:
 (9)
(9)
где Xt — неслучайная (детерминированная) величина, а Yt, et — случайные величины. Переменная Yt называется объясняемой, зависимой или результативным признаком, а Xt — объясняющей, независимой, регрессором или факторным признаком. Переменная et выступает в качестве ошибки в объяснении зависимости Yt от Xt. Поскольку обе случайные величины Yt, et отличаются друг от друга константой, их функции распределения соответствуют друг другу. Уравнение (9) называют также регрессионным уравнением.
Базовые гипотезы нормальной линейной регрессионной модели следующие:
1) Xt — детерминированная величина;
2)  — не зависит от t; (10)
— не зависит от t; (10)
3)  при t ¹ s, некоррелированность ошибок для разных наблюдений;
при t ¹ s, некоррелированность ошибок для разных наблюдений;
где E — символ математического ожидания, а V — символ дисперсии.
Условие независимости дисперсии 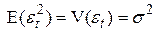 от номера реализации t = 1,…, n называется гомоскедастичностью (homoscedasticity). Случай, когда условие гомоскедастичности не выполняется, называется гетероскедастичностью.
от номера реализации t = 1,…, n называется гомоскедастичностью (homoscedasticity). Случай, когда условие гомоскедастичности не выполняется, называется гетероскедастичностью.
Условие  , t ¹ s означает отсутствие корреляции ошибок для различных наблюдений. Эти условия часто нарушаются, когда нашими данными являются временные ряды. Если это условие не выполняется, то говорят об автокорреляции ошибок.
, t ¹ s означает отсутствие корреляции ошибок для различных наблюдений. Эти условия часто нарушаются, когда нашими данными являются временные ряды. Если это условие не выполняется, то говорят об автокорреляции ошибок.
В нашем распоряжении находятся данные наблюдений (Xt, Yt), t = 1,…, n и модель (9), и условия (10). Оценим параметры a, b и s 2 наилучшим способом. Вся проблема состоит в том, какой смысл вкладывать в слово “наилучшая”.
Теорема Гаусса-Маркова. При выборе модели f (X) = a + bX оценки 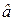 ,
, 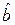 , полученные по методу наименьших квадратов (МНК) имеют наименьшую дисперсию в классе всех линейных несмещенных оценок, т.е. являются эффективными.
, полученные по методу наименьших квадратов (МНК) имеют наименьшую дисперсию в классе всех линейных несмещенных оценок, т.е. являются эффективными.
Тема 3. Классическая нормальная линейная модель множественной регрессии. Предпосылки регрессионного анализа. Адекватность, значимость и точность модели. Оценка значимости коэффициентов регрессии. Уравнение регрессии в стандартизованной форме. Пример построения линейной модели множественной регрессии. Экономическая интерпретация параметров модели.
Экономические явления определяются, как правило, большим числом совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости одной переменной Y от нескольких объясняющих переменных X1, X2, …,Xn. Эта задача решается с помощью множественного регрессионного анализа.
Построение уравнения множественной регрессии начинается с решения вопроса о спе-цификации модели, включающего отбор факторов и выбор вида уравнения регрессии. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:
- они должны быть количественно измеримы (качественным факторам необходимо придать количественную определенность);
- между факторами не должно быть высокой корреляционной, а тем более функциональной зависимости, т.е. наличия мультиколлинеарности.
Включение в модель мультиколлинеарных факторов может привести к следующим последствиям:
· затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом виде», поскольку факторы связаны между собой; параметры линейной регрессии теряют экономический смысл;
· оценки параметров ненадежны, имеют большие стандартные ошибки и меняются с изменением объема наблюдений.
Пусть Y=(y1, y2, …,yn)т – матрица-столбец значений зависимой переменной размера n;
 – матрица значений объясняющих переменных;
– матрица значений объясняющих переменных;
β=(β0, β1, …,βm)т – матрица-столбец (вектор) параметров размера m+1;
ε=(ε1, …, εn)т – матрица-столбец (вектор) остатков размера n.
Тогда в матричной форме модель множественной линейной регрессии запишется следующим образом:
Y = Xβ + ε. (1)
Оценка этой модели по выборке:
Y = Xb + e, (2)
где b=(b0, b1, …,bm)т – матрица-столбец (вектор) оценок параметров размера
Для оценки параметров уравнения регрессии (вектора b) применяется метод наименьших квадратов (МНК). При этом делаются определенные предпосылки:
1. В модели (1) ε – случайный вектор, X – неслучайная (детерминированная) матрица.
2. Математическое ожидание величины остатков равно нулю: М(ε)= 0 n.
3. Дисперсия остатков εi постоянна для любого i (условие гомоскедастичности), остатки εi и εj при i≠j не коррелированы: М(εεТ)=σ2En.
4. ε – нормально распределенный случайный вектор, т.е. ε~N(0 n; σ2En).
5. r(X) = m+1<n. Столбцы матрицы Х должны быть линейно независимыми (ранг матрицы Х максимальный, а число наблюдений n превосходит ранг матрицы).
Модель (1), в которой зависимая переменная, остатки и объясняющие переменные удовлетворяют предпосылкам 1-5 называется классической нормальной линейной моделью множественной регрессии. Если не выполняется только предпосылка 4, то модель называется классической линейной моделью множественной регрессии (КЛММР).
Согласно методу наименьших квадратов неизвестные параметры выбираются таким образом, чтобы сумма квадратов отклонений фактических значений от значений, найденных по уравнению регрессии, была минимальной:
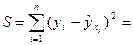 (Y-Xb)(Y-Xb)Т → min
(Y-Xb)(Y-Xb)Т → min
Решением этой задачи является вектор b = (XТX)-1XТY.
Полученная оценка параметров модели должна быть несмещенной, состоятельной и эффективной, то есть иметь наименьшее рассеяние относительно оцениваемого параметра. По теореме Гаусса-Маркова при выполнении предпосылок регрессионного анализа оценка метода наименьших квадратов b = (XТX)-1XТY является наиболее эффективной, то есть обладает наименьшей дисперсией в классе линейных несмещенных оценок.
Оценка адекватности модели множественной регрессии.
Одной из наиболее эффективных оценок адекватности модели является коэффициент детерминации R2, определяемый формулой:
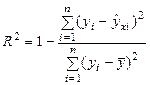 .
.
Коэффициент детерминации характеризует долю вариации зависимой переменной, обусловленной регрессией или изменчивостью объясняющих переменных. Чем ближе R2 к единице, тем лучше построенная регрессионная модель описывает зависимость между объясняющими и зависимой переменной.
Следует иметь в виду, что при включении в модель новой объясняющей переменной, коэффициент детерминации увеличивается, хотя это и не обязательно означает улучшение качества регрессионной модели. В этой связи лучше использовать скорректированный (поправленный) коэффициент детерминации  , рассчитываемый по формуле:
, рассчитываемый по формуле:
 ,
,
где n – число наблюдений,
m – число параметров при переменных x.
Из формулы следует, что с включением в модель дополнительных переменных разница между значениями  и R2 увеличивается. Таким образом, скорректированный коэффициент детерминации может уменьшаться при добавлении в модель новой объясняющей переменной, не оказывающей существенного влияния на результативный признак.
и R2 увеличивается. Таким образом, скорректированный коэффициент детерминации может уменьшаться при добавлении в модель новой объясняющей переменной, не оказывающей существенного влияния на результативный признак.
Но использование только коэффициента детерминации для выбора наилучшего уравнения регрессии может оказаться недостаточным.
Средняя относительная ошибка аппроксимации рассчитывается по формуле:
 .
.
Значимость уравнения регрессии в целом сводится к проверке гипотезы об одновременном равенстве нулю всех коэффициентов регрессии при факторных признаках, т.е. гипотезы:
Н 0: b 1 = b 2 =…= bm =0.
Если данная гипотеза не отклоняется, то делается вывод о том, что совокупное влияние всех факторных признаков х 1, х 2,… х m, включенных в модель, на зависимую переменную y можно считать статистически несущественным. Проверка данной гипотезы осуществляется на основе дисперсионного анализа.
Основной идеей дисперсионного анализа является разложение общей суммы квадратов отклонений результативной переменной y от среднего значения  на «объясненную» и «остаточную»:
на «объясненную» и «остаточную»:
 .
.
| Общая сумма квадратов отклонений | Сумма квадратов отклонений, объясненная регрессией | Остаточная сумма квадратов отклонений |
Для приведения дисперсий к сопоставимому виду, определяют дисперсии на одну степень свободы. Результаты вычислений заносят в специальную таблицу дисперсионного анализа:
| Компоненты дисперсии | Сумма квадратов | Число степеней свободы | Оценка дисперсии на одну степень свободы |
| Объясненная | 
| m | 
|
| Остаточная | 
| n – m – 1 | 
|
| Общая | 
| n – 1 | - |
В данной таблице n – число наблюдений, m – число параметров при переменных x.
Сравнивая полученные оценки объясненной и остаточной дисперсии на одну степень свободы, определяют значение F-критерия Фишера, используемого для оценки значимости уравнения регрессии:
 .
.
С помощью F -критерия проверяется нулевая гипотеза о равенстве дисперсий Н0: sR2 = s2.
Если нулевая гипотеза справедлива, то объясненная и остаточная дисперсии не отличаются друг от друга. Для того, чтобы уравнение регрессии было значимо в целом (гипотеза Н0 была опровергнута) необходимо, чтобы объясненная дисперсия превышала остаточную в несколько раз. Критическое значение F -критерия определяется по таблице Фишера-Снедекора.
Расчетное значение сравнивается с табличным, и если оно превышает табличное (Fрасч >Fтабл), то гипотеза Н0 отвергается, и уравнение регрессии признается значимым.
Если Fрасч <Fтабл, то уравнение регрессии считается статистически незначимым. Нулевая гипотеза Н0 не может быть отклонена.
Расчетное значение F -критерия связано с коэффициентом детерминации R2
следующим соотношением:
 ,
,
где m – число параметров при переменных x;
n – число наблюдений.
Оценка значимости коэффициентов регрессии сводится к проверке гипотезы о
равенстве нулю коэффициента регрессии при соответствующем факторном признаке,
т.е. гипотезы:
Н 0: b j =0.
Проверка гипотезы проводится с помощью t -критерия Стьюдента. Для этого определяется расчетное значение t -критерия:
 ,
,
где bj – коэффициент регрессии при xi;
 – средняя квадратическая ошибка коэффициента регрессии bj.
– средняя квадратическая ошибка коэффициента регрессии bj.
сравнивается с табличным tтабл при заданном уровне значимости α и числе степеней свободы (n -2).
Если расчетное значение превышает табличное, то гипотезу о несущественности коэффициента регрессии можно отклонить.
Рассмотрим интерпретацию параметров модели линейной множественной регрессии. В линейной модели множественной регрессии  = b 0 + b 1∙ x 1 + … + b m∙ x m коэффициенты регрессии bj характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленных на среднем уровне.
= b 0 + b 1∙ x 1 + … + b m∙ x m коэффициенты регрессии bj характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленных на среднем уровне.
На практике часто бывает необходимо сравнить влияние на зависимую переменную различных объясняющих переменных, когда последние выражаются разными единицами измерения. В этом случае используют стандартизованные коэффициенты регрессии βj и коэффициенты эластичности Эj (j=1, 2, …, m).
Уравнение регрессии в стандартизованной форме:
 ,
,
где  ,
,  – стандартизованные переменные.
– стандартизованные переменные.
В результате такого нормирования средние значения всех стандартизованных переменных равны нулю, а дисперсии равны единице, т.е. 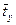 =
= =…=
=…= =0,
=0,  =
= =…=
=…= =1.
=1.
Коэффициенты «чистой» регрессии связаны со стандартизованными коэффициентами следующим соотношением:  .
.
Стандартизованные коэффициенты показывают, на сколько стандартных отклонений (сигм) изменится в среднем результат, если соответствующий фактор xi изменится на одно стандартное отклонение (одну сигму) при неизменном среднем уровне других факторов. Сравнивая стандартизованные коэффициенты друг с другом, можно ранжировать факторы по силе их воздействия на результат.
Средние коэффициенты эластичности вычисляются по формуле:
 .
.
Коэффициент эластичности показывает, на сколько процентов (от средней) изменится в среднем Y при увеличении только фактора Xj на 1%.
Рассмотрим пример построения модели множественной регрессии с помощью средств приложения Microsoft Excel.
Пример 1. По данным, представленным в таблице 2, изучается зависимость балансовой прибыли предприятия торговли  (тыс. руб.) от следующих факторов:
(тыс. руб.) от следующих факторов:
 - объем товарных запасов, тыс. руб.;
- объем товарных запасов, тыс. руб.;
 - фонд оплаты труда, тыс. руб.;
- фонд оплаты труда, тыс. руб.;
 - издержки обращения, тыс. руб.;
- издержки обращения, тыс. руб.;
 - объем продаж по безналичному расчету, тыс. руб.
- объем продаж по безналичному расчету, тыс. руб.
Таблица 2
| Месяц | Y | Х1 | Х2 | Х3 | Х4 |
| 41321,57 | 300284,10 | 19321,80 | 42344,92 | 100340,02 | |
| 40404,27 | 494107,21 | 20577,92 | 49000,43 | 90001,35 | |
| 37222,12 | 928388,75 | 24824,91 | 50314,52 | 29301,98 | |
| 37000,80 | 724949,11 | 28324,87 | 48216,41 | 11577,42 | |
| 29424,84 | 730855,33 | 21984,07 | 3301,30 | 34209,84 | |
| 20348,19 | 2799881,13 | 11000,02 | 21284,21 | 29300,00 | |
| 11847,11 | 1824351,20 | 4328,94 | 28407,82 | 19531,92 | |
| 14320,64 | 1624500,80 | 7779,41 | 40116,00 | 17343,20 | |
| 18239,46 | 1115300,93 | 18344,11 | 32204,98 | 4391,00 | |
| 22901,52 | 1200947,52 | 20937,31 | 30105,29 | 14993,25 | |
| 27391,92 | 1117850,93 | 27344,30 | 40294,40 | 104300,00 | |
| 44808,37 | 1379590,02 | 31939,52 | 42239,79 | 119804,33 | |
| 40629,28 | 588365,77 | 29428,60 | 55584,35 | 155515,15 | |
| 31324,80 | 434281,91 | 30375,82 | 49888,17 | 60763,19 | |
| 34847,92 | 1428243,59 | 33000,94 | 59866,55 | 8763,25 | |
| 33241,32 | 1412181,59 | 31322,60 | 49975,79 | 4345,42 | |
| 29971,34 | 1448274,10 | 20971,82 | 3669,92 | 48382,15 | |
| 17114,90 | 4074616,71 | 11324,93 | 26032,95 | 10168,00 | |
| 8944,94 | 1874298,99 | 8341,52 | 29327,21 | 22874,40 | |
| 17499,58 | 1525436,47 | 10481,14 | 40510,01 | 29603,05 | |
| 19244,80 | 1212238,89 | 18329,90 | 37444,69 | 16605,16 | |
| 34958,32 | 1154327,22 | 29881,52 | 36427,22 | 32124,63 | |
| 44900,83 | 1173125,03 | 34928,60 | 51485,62 | 200485,00 | |
| 57300,25 | 1435664,93 | 41824,92 | 49959,92 | 88558,62 |
Задание:
1. Для заданного набора данных постройте линейную модель множественной
регрессии.
2. Оцените точность и адекватность построенного уравнения регрессии.
3. Выделите значимые и незначимые факторы в модели.
4. Постройте уравнение регрессии со статистически значимыми факторами. Дайте экономическую интерпретацию параметров модели.
Решение.
Для получения отчета по построению модели в среде EXCEL необходимо выполнить ледующие действия:
1. В меню Сервис выбираем строку Анализ данных. На экране появится окно

Рис. 1.
2. В появившемся окне выбираем пункт Регрессия. Появляется диалоговое окно, в котором задаем необходимые параметры (рис. 2).

Рис. 2.
3. Диалоговое окно рис. 2 заполняется следующим образом:
Входной интервал  – диапазон (столбец), содержащий данные со значениями объясняемой переменной;
– диапазон (столбец), содержащий данные со значениями объясняемой переменной;
Входной интервал 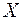 – диапазон (столбцы), содержащий данные со значениями объясняющих переменных.
– диапазон (столбцы), содержащий данные со значениями объясняющих переменных.
Метки – флажок, который указывает, содержат ли первые элементы отмеченных диапазонов названия переменных (столбцов) или нет;
Константа-ноль - флажок, указывающий на наличие или отсутствие свободного члена в уравнении регрессии ( );
);
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона, в котором будет сохранен отчет по построению модели;
Новый рабочий лист – можно задать произвольное имя нового листа,
в котором будет сохранен отчет.
Если необходимо получить значения и графики остатков ( ), установите соответствующие флажки в диалоговом окне. Нажмите на кнопку OK.
), установите соответствующие флажки в диалоговом окне. Нажмите на кнопку OK.
Вид отчета о результатах регрессионного анализа представлен на рис. 3.


Рис. 3.
Рассмотрим таблицу " Регрессионная статистика ".
Множественный R – это  , где
, где  – коэффициент детерминации.
– коэффициент детерминации.
R-квадрат – это  . В нашем примере значение
. В нашем примере значение  = 0,8178 свидетельствует о том, что изменения зависимой переменной
= 0,8178 свидетельствует о том, что изменения зависимой переменной  (балансовой прибыли) в основном (на 81,78%) можно объяснить изменениями включенных в модель объясняющих переменных – Х1, Х2, Х3, Х4. Такое значение свидетельствует об адекватности модели.
(балансовой прибыли) в основном (на 81,78%) можно объяснить изменениями включенных в модель объясняющих переменных – Х1, Х2, Х3, Х4. Такое значение свидетельствует об адекватности модели.
Нормированный R-квадрат – поправленный (скорректированный по числу степеней свободы) коэффициент детерминации.
Стандартная ошибка регрессии  , где
, где  – необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии); n – число
– необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии); n – число
наблюдений (в нашем примере равно 24), m – число объясняющих переменных (в нашем примере равно 4).
Наблюдения – число наблюдений n.
Рассмотрим таблицу с результатами дисперсионного анализа.
df – degrees of freedom – число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант (m +1).
SS – sum of squares – сумма квадратов (регрессионная (RSS –regression sum of squares), остаточная (ESS – error sum of squares) и общая (TSS – total sum of squares), соответственно).
MS – mean sum - сумма квадратов на одну степень свободы.
F - расчетное значение F -критерия Фишера. Если нет табличного значения, то для проверки значимости уравнения регрессии в целом можно посмотреть Значимость F. На уровне значимости  уравнение регрессии признается значимым в целом, если Значимость
уравнение регрессии признается значимым в целом, если Значимость  , и незначимым, если Значимость
, и незначимым, если Значимость  .
.
Для нашего примера имеем следующие значения:
| df | SS | MS | F | Значи-мость F | |
| Регрессия | m = 4 |
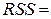 2,82Е+09 2,82Е+09
|  7,04Е+08 7,04Е+08
|  = 21,32
= 21,32
| 8,28Е-07 |
| Остаток | n– m–1=19 |
 6,27Е+08 6,27Е+08
|  3,30Е+07 3,30Е+07
| ||
| Итого | n – 1 = 23 |  3,44Е+09 3,44Е+09
|
В нашем случае расчетное значение F -критерия Фишера составляет 21,32. Значимость F = 8,28Е-07, что меньше 0,05. Таким образом, полученное уравнение в целом значимо.
В последней таблице приведены значения параметров (коэффициентов) модели, их стандартные ошибки и расчетные значения t-критерия Стьюдента для оценки значимости отдельных параметров модели.
| Коэффи-циенты | Стандартная ошибка | t- статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y | b0 = = 7825,51 |  5350,78 5350,78
|  =7825,51/5350,78==1,4625
=7825,51/5350,78==1,4625
| 0,1599 | -3373,80 19024,83 19024,83
| |
| Х1 | b1 = = -0,00098 |  0,00172 0,00172
|  -0,569 -0,569
| 0,5762 | -0,0046 0,0026 0,0026
| |
| Х2 | b2 = = 0,8806 |  0,15891 0,15891
|  5,5417 5,5417
| 0,00002 | 0,5480 1,2132 1,2132
| |
| Х3 | b3 = 0,0094 |  0,09754 0,09754
|  0,0961 0,0961
| 0,9244 | -0,1948 0,2135 0,2135
| |
| Х4 | b4 = 0,0617 |  0,02647 0,02647
| 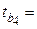 2,3312 2,3312
| 0,0309 | 0,0063 0,1171 0,1171
|
Анализ таблицы для рассматриваемого примера позволяет сделать вывод о том, что на уровне значимости  значимыми оказываются лишь коэффициенты при факторах Х2 и Х4., так как только для них Р-значение меньше 0,05. Таким образом, факторы Х1 и Х3. не существенны, и их включение в модель нецелесообразно.
значимыми оказываются лишь коэффициенты при факторах Х2 и Х4., так как только для них Р-значение меньше 0,05. Таким образом, факторы Х1 и Х3. не существенны, и их включение в модель нецелесообразно.
Поскольку коэффициент регрессии в эконометрических исследованиях имеют четкую экономическую интерпретацию, то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, как например, -0,1948 0,2135. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть. Это также подтверждает вывод о статистической незначимости коэффициентов регрессии при факторах Х1 и Х3.
0,2135. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть. Это также подтверждает вывод о статистической незначимости коэффициентов регрессии при факторах Х1 и Х3.
Исключим несущественные факторы Х1 и Х3 и построим уравнение зависимости  (балансовой прибыли) от объясняющих переменных Х2, и Х4. Результаты регрессионного анализа приведены в таблице 3.
(балансовой прибыли) от объясняющих переменных Х2, и Х4. Результаты регрессионного анализа приведены в таблице 3.
Таблица 3
| ВЫВОД ИТОГОВ | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,9024465 | |||||
| R-квадрат | 0,8144098 | |||||
| Нормированный R-квадрат | 0,7967345 | |||||
| Стандартная ошибка | 5515,53984 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 46,076253 | 2,08847E-08 | ||||
| Остаток | 638844774,1 | 30421179,72 | ||||
| Итого | ||||||
| Коэффици-енты | Стандартная ошибка | t- статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 5933,1025 | 2844,611998 | 2,085733487 | 0,0493883 | 17,40698 | 11848,798 |
| Х2 | 0,9162546 | 0,132496978 | 6,915286693 | 7,834E-07 | 0,640712 | 1,1917972 |
| Х4 | 0,0645183 | 0,024940789 | 2,58686011 | 0,0172036 | 0,012651 | 0,1163856 |
Оценим точность и адекватность полученной модели.
Значение  = 0,8144 свидетельствует о том, что вариация зависимой переменной
= 0,8144 свидетельствует о том, что вариация зависимой переменной  (балансовой прибыли) по-прежнему в основном (на 81,44%) можно объяснить вариацией включенных в модель объясняющих переменных – Х2, и Х4. Это свидетельствует об адекватности модели.
(балансовой прибыли) по-прежнему в основном (на 81,44%) можно объяснить вариацией включенных в модель объясняющих переменных – Х2, и Х4. Это свидетельствует об адекватности модели.
Значение поправленного коэффициента детерминации (0,7967) возросло по сравнению с первой моделью, в которую были включены все объясняющие переменные (0,7794).
Стандартная ошибка регрессии во втором случае меньше, чем в первом
(5515 < 5745).
Расчетное значение F -критерия Фишера составляет 46,08. Значимость F = 2,08847E-08, что меньше 0,05. Таким образом, полученное уравнение в целом значимо.
Далее оценим значимость отдельных параметров построенной модели. Из таблицы 3 видно, что теперь на уровне значимости  все включенные в модель факторы являются значимыми: Р-значение < 0,05.
все включенные в модель факторы являются значимыми: Р-значение < 0,05.
Границы доверительного интервала для коэффициентов регрессии не содержат противоречивых результатов:
- с надежностью 0,95 (c вероятностью 95%) коэффициент b1 лежит в интервале 0,64 ≤ b1 ≤ 1,19;
- с надежностью 0,95 (c вероятностью 95%) коэффициент b2 лежит в интервале 0,01 ≤ b2 ≤ 0,12
Таким образом, модель балансовой прибыли предприятия торговли запишется в следующем виде:

Рассмотрим теперь экономическую интерпретацию параметров модели.
Коэффициент b1 = 0,916, означает, что при увеличении только фонда оплаты труда (Х2) на 1 тыс. руб. балансовая прибыль в среднем возрастает на 0,916 тыс. руб., а то, что коэффициент b2 = 0,065, означает, что увеличение только объема продаж по безналичному расчету (Х4) на 1 тыс. руб. приводит в среднем к увеличению балансовой прибыли на 0,065 тыс. руб. Как было отмечено выше, анализ P-значений показывает, что оба коэффициента значимы.¨
|
|
Дата добавления: 2014-01-07; Просмотров: 1484; Нарушение авторских прав?; Мы поможем в написании вашей работы!