Полиморфные структуры данных

Рассмотрим массив многоугольников:

poly_arr: ARRAY [POLYGON]

Когда некоторое значение x присваивается элементу этого массива, как в вызове

poly_arr.put (x, some_index)

(для некоторого допустимого значения индекса some_index), то спецификация класса ARRAY указывает, что тип присваиваемого значения должен быть согласован с типом фактического родового параметра:

class ARRAY [G] creation

...

feature - Изменение элемента

put (v: G; i: INTEGER) is

-- Присвоить v элементу с индексом i

...

end

Так как тип формального аргумента v, соответствующего x, в классе определен как G, а фактический родовой параметр, соответствующий G в вызове poly_arr, - это POLYGON, то тип x должен быть согласован с ним. Как мы видели, для этого x не обязан иметь тип POLYGON, подойдет любой потомок типа POLYGON.

Поэтому, если границы массива равны 1 и 4, то можно объявить некоторые сущности:

p: POLYGON; r: RECTANGLE; s: SQUARE; t: TRIANGLE

и, создав соответствующие объекты, можно выполнить операции

poly_arr.put (p, 1)

poly_arr.put (r, 2)

poly_arr.put (s, 3)

poly_arr.put (t, 4)

которые присвоят элементам массива ссылки на объекты различных типов.

Рис. 14.4. Полиморфный массив

На этом рисунке графические объекты представлены соответствующими геометрическими фигурами, а не обычными диаграммами объектов с набором их полей.Такие структуры данных, содержащие объекты разных типов, имеющих общего предка, называются полиморфными структурами данных. Далее будут рассмотрены многочисленные примеры таких структур. Массивы - это только одна из возможностей, полиморфными могут быть любые структуры контейнеров: списки, стеки и т.п.

Полиморфные структуры данных реализуют цель, сформулированную в начале лекции: объединение порождения и наследования для достижения максимальной гибкости и надежности. Имеет смысл напомнить рис. 10.1, иллюстрирующий эту мысль:

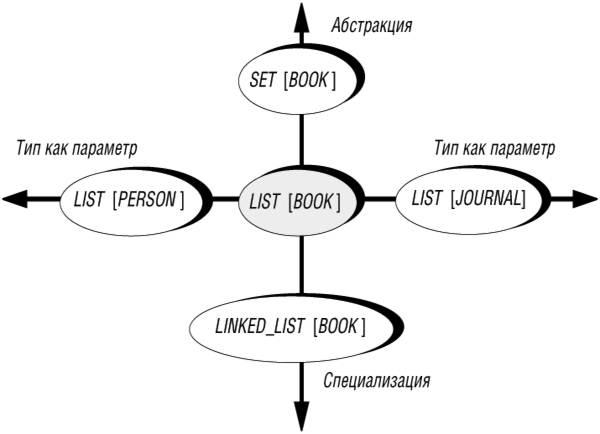
Рис. 14.5. Измерения обобщения

Типы, которые на рис. 10.1 неформально назывались SET_OF_BOOKS и т. п., заменены типами, выведенными из родового универсального типа, - SET [BOOK].

Такая комбинация универсальности и наследования является весьма сильным средством. Оно позволяет описывать структуру объектов с нужной степенью общности. Например,

LIST [RECTANGLE]: может содержать квадраты, но не треугольники.

LIST [POLYGON]: может содержать квадраты, прямоугольники, треугольники, но не круги.

LIST [FIGURE]: может содержать экземпляры любого типа из иерархии FIGURE, но не книги или банковские счета.

LIST [ANY]: может содержать объекты любого типа.

В последнем случае использован класс ANY, который условимся считать предком любого класса (он будет подробнее рассмотрен далее).

Варьируя место класса, выбираемого в качестве фактического родового параметра, в иерархии, можно точно установить границы типов объектов, допустимых в определяемом контейнере.

Дата добавления: 2014-01-07