Скрытие потомком

Своенравие полиморфизма

Не довольно ли примеров, подтверждающих практичность ковариации? Почему же кто-то рассматривает контравариантность, которая вступает в противоречие с тем, что необходимо на практике (если не принимать во внимание поведения некоторых молодых людей)? Чтобы понять это, рассмотрим проблемы, возникающие при сочетании полиморфизма и стратегии ковариантности. Придумать вредительскую схему несложно, и, возможно, вы уже создали ее сами:

s: SKIER; b: BOY; g: GIRL

...

create b; create g;-- Создание объектов BOY и GIRL.

s:= b; -- Полиморфное присваивание.

s.share (g)

Результат последнего вызова, вполне возможно приятный для юношей, - это именно то, что мы пытались не допустить с помощью переопределения типов. Вызов share ведет к тому, что объект BOY, известный как b и благодаря полиморфизму получивший псевдоним s типа SKIER, становится соседом объекта GIRL, известного под именем g. Однако вызов, хотя и противоречит правилам общежития, является вполне корректным в программном тексте, поскольку share -экспортируемый компонент в составе SKIER, а GIRL, тип аргумента g, совместим со SKIER, типом формального параметра share.

Схема с параллельной иерархией столь же проста: заменим SKIER на SKIER1, вызов share - на вызов s.accommodate (gr), где gr - сущность типа GIRL_ROOM. Результат - тот же.

При контравариантном решении этих проблем не возникало бы: специализация цели вызова (в нашем примере s) требовала бы обобщения аргумента. Контравариантность в результате ведет к более простой математической модели механизма: наследование - переопределение - полиморфизм. Данный факт описан в ряде теоретических статей, предлагающих эту стратегию. Аргументация не слишком убедительна, поскольку, как показывают наши примеры и другие публикации, контравариантность не имеет практического использования.

В литературе для программистов нередко встречается призыв к методам, основанных на простых математических моделях. Однако математическая красота - всего лишь один из критериев ценности результата, - есть и другие - полезность и реалистичность.Поэтому, не пытаясь натянуть контравариантную одежду на ковариантное тело, следует принять ковариантную действительность и искать пути устранения нежелательного эффекта.

Прежде чем искать решение проблемы ковариантности, рассмотрим еще один механизм, способный в условиях полиморфизма привести к нарушениям типа. Скрытие потомком (descendant hiding) - это способность класса не экспортировать компонент, полученный от родителей.

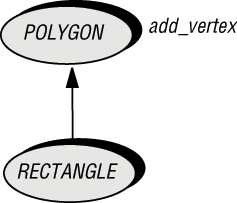
Рис. 17.8. Скрытие потомком

Типичным примером является компонент add_vertex (добавить вершину), экспортируемый классом POLYGON, но скрываемый его потомком RECTANGLE (ввиду возможного нарушения инварианта - класс хочет оставаться прямоугольником):

class RECTANGLE inherit

POLYGON

export NONE add_vertex end

feature

...

invariant

vertex_count = 4

end

Не программистский пример: класс "Страус" скрывает метод "Летать", полученный от родителя "Птица".

Давайте на минуту примем эту схему такой, как она есть, и поставим вопрос, будет ли легитимным сочетание наследования и скрытия. Моделирующая роль скрытия, подобно ковариантности, нарушается из-за трюков, возможных из-за полиморфизма. И здесь не трудно построить вредоносный пример, позволяющий, несмотря на скрытие компонента, вызвать его и добавить прямоугольнику вершину:

p: POLYGON; r: RECTANGLE

...

create r; -- Создание объекта RECTANGLE.

p:= r; -- Полиморфное присваивание.

p.add_vertex (...)

Так как объект r скрывается под сущностью p класса POLYGON, а add_vertex экспортируемый компонент POLYGON, то его вызов сущностью p корректен. В результате выполнения в прямоугольнике появится еще одна вершина, а значит, будет создан недопустимый объект.

Корректность систем и классов

Для обсуждения проблем ковариантности и скрытия потомком нам понадобится несколько новых терминов. Будем называть классово-корректной (class-valid) систему, удовлетворяющую трем правилам описания типов, приведенным в начале лекции. Напомним их: каждая сущность имеет свой тип; тип фактического аргумента должен быть совместимым с типом формального, аналогичная ситуация с присваиванием; вызываемый компонент должен быть объявлен в своем классе и экспортирован классу, содержащему вызов.

Система называется системно-корректной (system-valid), если при ее выполнении не происходит нарушения типов.

В идеале оба понятия должны совпадать. Однако мы уже видели, что классово-корректная система в условиях наследования, ковариантности и скрытия потомком может не быть системно-корректной. Назовем такую ошибку нарушением системной корректности (system validity error).

Дата добавления: 2014-01-07