Работа по перемещению заряда в электрическом поле

Поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри поверхности, деленной на электрическую постоянную

Доказательство проведем в несколько этапов.

1. Рассмотрим замкнутую поверхность в виде сферы радиуса r, в центр которой помещен точечный заряд q (рис. 2.6).

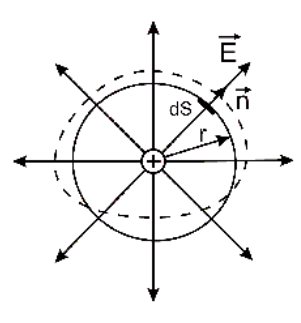
Рис.2.6

Напряженность электрического поля, созданного точечным зарядом в вакууме, вычисляется по формуле (2.4) при ε = 1

.

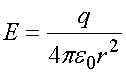Для сферы 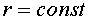, следовательно, 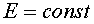, а также , так как 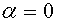. Поток вектора 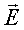в этом случае равен

Интеграл 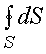равен площади сферы

.

Тогда поток вектора 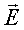равен

.

Ответ сравните с формулой (2.11) и убедитесь, что теорема доказана. Напомним, что поток пропорционален числу силовых линий, пронизывающих замкнутую поверхность.

2. Если замкнутая поверхность отличается от сферы (см. рис. 2.6, пунктирная линия), то поток вектора 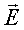не изменится, так как не изменяется число силовых линий, пронизывающих эту поверхность.

3. Если внутри замкнутой поверхности находится не один заряд, а несколько, то результирующая напряженность электрического поля находится по принципу суперпозиции (2.8). Тогда потоки и заряды складываются алгебраически, т. е. с учетом знаков, и теорема Гаусса, формула (2.11), оказывается справедливой.

Теорема Гаусса применяется для вычисления электрических полей, созданных протяженными зарядами, например, заряженной нитью, плоскостью и т. д. С помощью теоремы Гаусса получены формулы (2.5), (2.6) и (2.7).

Покажем, что электростатическое поле является потенциальным, а кулоновские силы - консервативными. Для этого рассчитаем работу, совершаемую электростатическим полем положительного точечного заряда q, по перемещению другого положительного точечного заряда q ₀ из точки 1 в точку 2 (рис. 2.7).

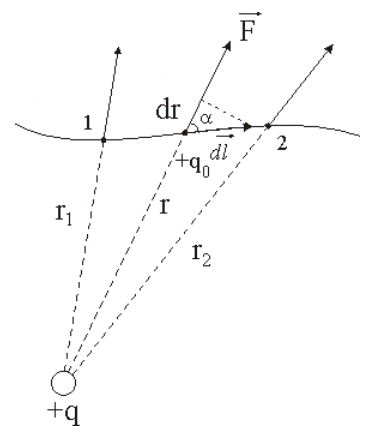
Рис.2.7

В процессе перемещения заряда q ₀ сила взаимодействия между зарядами будет изменяться, так как она зависит от расстояния между зарядами (формула (2.2))

.

Элементарную работу найдем по формуле: . Учтем, что 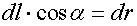(рис. 2.7).

Работу переменной силы будем определять по формуле (1.27):

Из формулы (2.12) видно, что работа не зависит от формы траектории и определяется только начальным и конечным положением пробного заряда. Следовательно, электростатическое поле является потенциальным, и в нем действуют консервативные силы, работа которых равна убыли потенциальной энергии (формула (1.33). Тогда

Дата добавления: 2014-01-07