Ж – состояние при воздействии вынужденных перемещений основания

этой нагрузки может быть принята площадь контакта балки с основанием, заменяемая в расчетной схеме стержнем. Таким образом, интенсивность распределенной нагрузки в формуле Б.Н. Жемочкина будет равна 1/(b × c), где b – ширина подошвы балки; с – расстояние между стержнями, моделирующими связь балки с основанием. Перемещение основания от действия неизвестной силы Zj = 1 по направлению силы Zi (рис. 2.5 в) определится формулой:

 o =

1 -  2

F ç b,

x j - xi ö

÷

.

(2.19)

æ

ij  × E × c ç c c ÷

è ø

где функция F определяется по таблице 7.1 лекции №7 (см. курс "Механика грунтов").

Разрешающие уравнения задачи будет иметь вид:

n b

å Z j × (ij

j =1

n

+ ij

) +  × xi + s + D i p + D i D

n

= 0;

o

(2.20)

å Z j + å Z p

j =1

= 0;

å Z j x j + å M p

j =1

= 0,

i = 1L n.

j

где ib

– перемещение балки от неизвестной силы Zj = 1 по направлению

силы Zj (рис. 2.5 в);  xi – перемещение по направлению силы Zi от углового перемещения балки в заделке  (рис. 2.5 г); s – перемещение по направлению силы Zi от линейного перемещения балки в заделке s (рис. 2.5 д); ip - перемещение по направлению силы Zi от внешней нагрузки (рис. 2.5 е); i - перемещение по направлению силы Zi от вынужденных перемещений основания (рис. 2.5 ж); xi, xj – координаты точек приложения сил Zi и Zj; Zp, Mp – соответственно сумма проекций сил и моментов сил от действующей нагрузки на вертикальную ось и относительно заделки на левом конце балки.

Решением системы уравнений (2.20) являются величины сил взаимодействия балки с основанием Zi. Деление указанных сил на площадь их распределения bc дает величины отпоров основания по подошве балки, возникающих при действии на балку эксплуатационных нагрузок. При известных отпорах основания рассматриваемая конструкция становится статически определимой, в связи с чем не возникает трудностей в определении внутренних усилий в балке и в назначении по этим усилиям ее конструктивных параметров (размеров поперечного сечения, армирования и т.п.).

Первое уравнение в системе уравнений (2.20) можно представить в матричной форме:

[  b ]+ [ 

o ] { Z }+ { x }  + {1} s + {D

}+ {D

} = 0,

(2.21)

ij ij i i

b

ip i D

o

где [ ij ] – матрица податливости балки; [ ij ] – матрица податливости

основания.

Из анализа уравнения (2.21) можно сформулировать следующие особенности расчета конструкций на упругом основании: при расчете конструкций на упругом основании матрица податливости системы представляет собой алгебраическую сумму матриц податливости конструкции и матрицы податливости основания. Для модели общих деформаций, например, для модели линейно-деформируемого

полупространства, матрица податливости основания является полной симметричной матрицей. Для модели местных деформаций, например, для модели Винклера, матрица податливости основания является диагональной матрицей, т. е. элементы этой матрицы, расположенные не на диагонали, равны нулю.

Расчет плит на упругом основании по методу Жемочкина выполняется по аналогичному алгоритму с учетом координаты y в плоскости плиты. При этом для вычисления коэффициентов матрицы податливости основания используется формула (7.2), приведенная в лекции №7 (см. курс "Механика грунтов").

3. Расчет рам на упругом основании. В расчетной схеме рамы на упругом основании (рис. 2.4) работа грунтового основания моделируется стержневыми конечными элементами, жестко сопрягаемыми со стаканной частью фундамента и имеющими неподвижные закрепления в опорных сечениях (рис. 2.6).

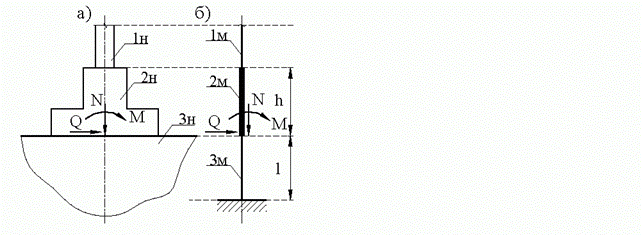Рис. 2.6. Стержневая модель грунтового основания: а – натурная конструкция; б – стержневая модель; 1н – колонна; 2н – фундамент; 3н – грунтовое основание; 1м – стержневая

модель колонны; 2м – стержневая модель фундамента; 3м – стержневая модель грунтового основания.

Жесткости стержней, моделирующих работу грунтового основания, назначаются из условий адекватности перемещений фундамента на грунтовом основании (или свайном основании) и верхнего сечения стержня эквивалентной жесткости при действии одних и тех же нагрузок. Здесь имеют место такие соотношения. Перемещения фундамента на упругом основании в соответствии с теорией коэффициента жесткости определяются формулами:

S = N;

Af × Cz

 = M;

I f × C

D = Q;

Af × Cx

(2.22)





C = Cz ×;

z

Cx = Cz

× (1 + ) × (1 -  ×  x),1 -  2

где Аf, If - соответственно площадь подошвы фундамента и момент инерции этой площади относительно оси, нормальной к плоскости изгиба;

Сz - коэффициент жесткости основания при равномерном сжатии, определяемый как отношение давления по подошве фундамента к осадке фундамента при этом давлении (вычисляемой методом послойного суммирования или методом линейно-деформируемого слоя, если Аf >100 м2);  - коэффициент Пуассона; z, x,  - коэффициенты формы подошвы фундамента (см. лекцию №7 в курсе "Механика грунтов").

Перемещения верхнего сечения стержня, моделирующего работу грунтового основания, определяются в соответствии с инженерной теорией деформирования стержней формулами:

D l =

Nl;

EF

 = M × l

EI

Q × l 2

+;

2 × EI

D = Q × l +

GF

M × l 2

+

2 × EI

Q × l 3

,

3 × EI

(2.23)

где EF, EI, GF - соответственно осевая, изгибная и сдвиговая жесткости стержня, моделирующего работу грунтового основания; l - длина стержня, моделирующего работу грунтового основания.

Приравнивая соответствующие перемещения фундамента на упругом основании и верхнего сечения стержня, моделирующего работу грунтового основания, получаем три уравнения для определения четырех геометрических параметров стержня: трех жесткостей и длины. Принимая длину стержня l в качестве произвольного параметра, получим выражения для определения трех жесткостей сечения стержня:

EF = Af

× C z × l;

EI = I f

× C

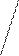æ

× (l +

Q

2 × M

× l 2);

3 ö

(2.24)

= ç 1

- 3× l

M Q + 2 × l ÷.

A

C

ø

GF l

ç

è f x

6 × EI ÷

Из полученных соотношений следует, что точное моделирование перемещений фундамента на упругом основании с помощью консольного стержневого элемента возможно только для определенного соотношения усилий M и Q, действующих в его верхнем сечении. Поскольку эти усилия заранее не известны, решение задачи будет связано с необходимостью организации итерационных процедур по уточнению жесткостных характеристик стержня. Чтобы этого избежать, попытаемся избавиться в

полученных выражениях от величин соотношения усилий в верхнем сечении стержня. Это возможно сделать, если принять длину стержня l значительно меньшей единицы. Тогда члены в формулах, содержащих l в степени, большей единицы, будут пренебрежимо малы по сравнению с членами, содержащими l в первой степени. С учетом сделанного допущения, получим:

EF» Af

Cz × l;

EI» I f

× C × l;

GF» Af

Cx × l;

l << 1.

(2.25)

На рис. 2.7 представлены результаты исследований влияния размеров фундаментов П – образной жесткой рамы на величины моментных нагрузок на фундаменты. Исследования выполнены с использованием расчетной модели грунтового основания по рис. 2.6. Установлено, что моментная нагрузка изменяется от минимального значения, соответствующего минимальному размеру подошвы фундамента из условия ограничения краевых давлений на основание, до максимального значения, соответствующего абсолютно жесткому основанию. При дальнейшем увеличении размеров фундамента моментная нагрузка не изменяется.

Рис. 2.7. Влияние размеров фундаментов на величину моментной нагрузки от надземного строения:

Мж – моментная нагрузка при абсолютно жестком основании; Вmin – минимальный размер подошвы фундамента из условия ограничения краевых давлений на основание.

Формулы (2.25) могут также использоваться при назначении параметров стержней эквивалентной жесткости для моделирования основания балок и плит, элементов конструкций заглубленных и подземных сооружений и т.п.

На рис. 2.8 представлена расчетная схема сваи как конструкции в деформируемой среде.

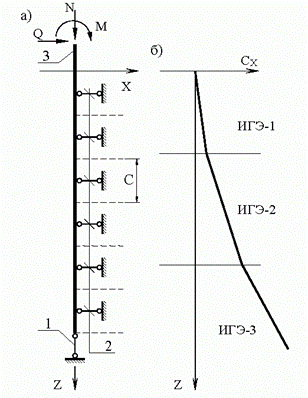
Рис. 2.8. К расчету свайного фундамента как конструкции в деформируемой среде: а – расчетная схема; б – график бокового коэффициента жесткости основания; 1 – стержень, моделирующий работу основания по подошве фундамента;

2 – стержни, моделирующие работу основания по боковой поверхности фундамента; 3 – стержень, моделирующий работу сваи.

Стержень поз. 1 моделирует осадку свайного фундамента. Его осевую жесткость следует вычислять по формуле (2.25) подстановкой в нее коэффициента жесткости основания Cz по формуле (2.22). При этом в формулах (2.25) и (2.22) следует принимать Af = Aуф (Aуф - площадь подошвы условного фундамента). Стержень поз. 2 моделирует горизонтальные перемещения деформируемой среды. Осевая жесткость этих стержней также определяется по формуле (2.25), в которую подставляется коэффициент жесткости основания Cx для боковой поверхности фундамента. Входящая в формулу (2.25) площадь контакта фундамента с основанием Af = cb, где с – расстояние между стержнями поз. 2; b – ширина сечения сваи. Таким образом, Af - это площадь контакта

боковой поверхности сваи с грунтом, заменяемая стержнем, моделирующим

работу деформируемой среды.

В результате расчета определяются усилия в стержнях поз. 1, 2, которые являются реакциями деформируемой среды. Делением этих усилий на площади Af, принятые в формуле (2.25) при вычислении осевых жесткостей стержней, получают контактные давления по боковой поверхности и пяте сваи. Указанные давления не должны превышать расчетного сопротивления грунта для подошвы условного фундамента или удовлетворять условию прочности для боковой поверхности сваи.

4. Континуальные конечно-элементные расчетные схемы фундаментов и сооружений на деформируемом основании. Расчет оснований, фундаментов и сооружений с использованием континуальных конечно-элементных расчетных схем относится к первой группе методов. В целом составление таких расчетных схем ни чем не отличается от принятого в теории расчета строительных конструкций. Для моделирования в расчетной схемы грунтов основания (рис. 2.9) используются пространственные или

плоские (плоская задача) треугольные и прямоугольные конечные элементы.

Для расчета оснований с использованием уравнений состояния теории пластичности рекомендуется применять октаэдрические и треугольные конечные элементы, напряженно- деформированное состояние в которых постулируется

однородным. Это необходимо

Рис. 2.9. Конечно-элементная

расчетная схема системы "основание – фундамент - стена крупнопанельного здания".

для привязки уравнений состояния к конкретным точкам среды, так как в процессе

нагружения изначально изотропная среда становится анизотропной (явление деформационной анизотропии). Деформационными характеристиками грунта в простейшем случае являются модуль деформации Е и коэффициент поперечной деформации . При использовании линейных моделей (см. лекцию №7 в курсе "Механика грунтов") грунтовый массив может рассматриваться как невесомый. Некоторые программные комплексы позволяют реализовать метод упругих решений для учета нелинейной работы материалов конструкций, в т.ч. и грунтов основания, моделируемых континуальными конечно-элементными расчетными схемами. В этом случае грунтовый массив должен загружаться силами собственного веса грунта. Для конечных элементов, расположенных ниже уровня грунтовых вод, при

определении объемных сил необходимо использовать удельный вес грунта во взвешенном состоянии sb.

Размеры грунтового массива в расчетной схеме должны назначаться по границам сжимаемой толщи основания. Указанные границы рекомендуется устанавливать предварительными расчетами с использованием методов механики грунтов. Закрепления на границах грунтового массива принимаются линейно неподвижными. Анализ результатов расчета предполагает проверку уровня напряжений в грунтовом массиве с использованием уравнений прочности Кулона - Мора. При этом вертикальные напряжения не должны превышать расчетного сопротивления грунта на заданной глубине массива. Если это условие не выполняется, расчет грунтового массива следует выполнять с учетом нелинейной работы грунтового основания. Если уровень напряженно-деформированного состояния в грунтовом массиве является недопустимым, производят корректировки, связанные с изменением конструктивных параметров фундаментов или их типа.

Довольно часто при анализе совместной работы системы "основание – фундамент – верхнее строение" определяющим является уровень напряженно-деформированного состояния надземных конструкций, поскольку именно это состояние определяет эксплуатационную пригодность сооружения. Например, в процессе эксплуатации здания (рис. 2.10) может произойти перераспределение отпора грунта под подошвой фундамента вследствие замачивания основания по краям здания. При этом максимальные давления на основание могут оставаться меньше допустимых. Следствием процесса перераспределения эпюры отпора грунта под подошвой фундамента является перераспределение нормальных напряжений в простенках первого этажа (см. график 2 на рис. 2.10).

При определенных условиях прочность простенков может оказаться недостаточной для восприятия дополнительных напряжений, вызванных перераспределением отпора грунта под зданием. Приведенный здесь пример свидетельствует о необходимости в отдельных случаях выполнения уточненных расчетов сооружений с учетом их взаимодействия с основанием и фундаментами для получения достоверных данных о напряженно-

деформированном состоянии надземных конструкций и предотвращения строительных аварий.

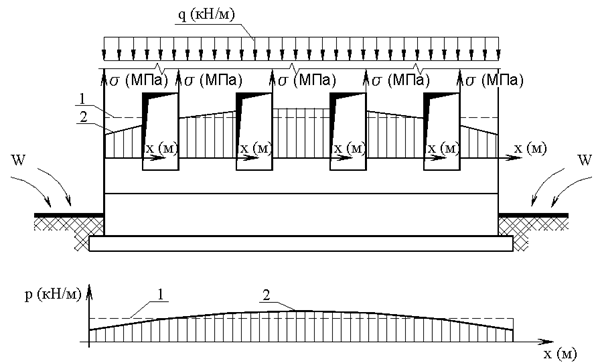
Рис. 2.10. Перераспределение напряжений в простенках стены бескаркасного здания, вызванное замачиванием грунтов основания у торцов: 1 – первоначальные эпюры отпора грунта и сжимающих напряжений в простенках; 2 – эпюры отпора грунта и напряжений в простенках после замачивания торцов здания;

q – распределенная нагрузка на стену; р – отпор грунта; s – вертикальные напряжения в простенках; W – направление замачивания грунтов основания.

Дата добавления: 2014-01-07