Горизонтальных и угловых колебаний фундамента (две степени свободы)

Рис. 8.2. Зависимость амплитуды колебаний фундаментов одной массы от площади опирания на основание: m – масса фундамента; А 1, А 2– площадь подошвы фундамента;

Z 0,1, Z 0,2– амплитуда колебаний; P sin t – динамическая нагрузка.

При действии по верху фундамента горизонтальной периодической нагрузки Px ×sin t (рис. 8.3) возникают горизонтальные и угловые колебания фундамента, амплитуды которых определяются по формулам:

X 0 =

K x

Px

- m ×  2

= Px;

x

C × A - m ×  2

(8.6)

F = Px × H =

Px × H,

K - I m

×  2

C × I f

- I m

×  2

где Н – плечо приложения силы Px относительно подошвы фундамента; Im – момент инерции массы всей установки относительно оси, проходящей через общий центр тяжести перпендикулярно плоскости колебаний (кг×м2 или кН×м×с2).

Фундаменты под электрические машины и турбоагрегаты при скорости вращения n > 1000 об/мин (f = 16,67 гц,  = 105 рад/с) на динамические нагрузки не рассчитываются, за исключением нагрузок пускового периода.

Расчет фундаментов на динамические нагрузки ударного действия. Динамические нагрузки ударного действия возникают при работе штамповочных и ковочных молотов. Молот состоит (рис. 8.4) из станины, подвижной части (молота), шабота, подшаботных прокладок, подшаботной плиты и фундамента.

Масса фундамента (т) и площадь подошвы фундамента определяются по эмпирическим формулам:

m f = 8 × (1 + ) × v × m 0- m 1;

A ³ 20 × (1 + ) × v × m 0;

Rd

(8.7)

v = 0,9 ×

2 × g × h,

где m0 и m1 – соответственно масса молота и масса станины с шаботом (т); v – скорость молота в момент, предшествующий удару (м/с); h – высота падения молота; g – ускорение свободного падения;  - коэффициент восстановления удара, зависящий от упругих свойств соударяющихся частей; Rd – расчетное сопротивление грунта; mf и A – соответственно масса фундамента с грунтом на его свесах и площадь подошвы фундамента.

Коэффициент восстановления удара  принимается: при штамповке

стальных изделий – 0,5; при штамповке

2

изделий из цветных металлов – 0; при

3 ковке – 0,25. Скорость молота и его масса

5 зависят от конструкции машины.

Различают легкие, средние и тяжелые

молоты. Для легких молотов (масса до

1 т) скорость в момент удара составляет 8 м/с. Масса средних молотов изменяется

Рис. 8.4. Конструктивные

элементы штамповочных и ковочных молотов: 1 – станина; 2 – подвижная часть (молот);

3 – шабот; 4 – подшаботная прокладка; 5 – подшаботная плита; 6 – фундамент.

от 1 до 3 т, а скорость составляет 7 м/с. Тяжелые молоты массой более 3 т имеют скорость 6,5 м/с. После назначения конструктивных параметров фундамента с учетом рекомендуемых параметров по

формулам (8.7) определяют амплитуду вертикальных колебаний фундамента:

Z = 0,2 × (1 +  ) × v × m,

Cz × A × m

(8.8)

где m – масса станины, молота, шабота и фундамента с грунтом на свесах;

Сz – коэффициент упругости основания по формулам (8.1).

Полученное значение амплитуды вертикальных колебаний фундамента сравнивается с допускаемой нормами величиной. Если установленные нормами ограничения амплитуды вертикальных колебаний не выполняются, производят переопределение конструктивных параметров фундамента, например, увеличивают площадь его подошвы, увеличивают жесткость основания и т.п.

Распространение колебаний в грунтовом массиве. Динамические нагрузки на фундаменты возбуждают колебания в окружающем его грунтовом массиве (рис. 8.5). При этом оказываются динамические воздействия на расположенные в непосредственной близости здания и сооружения. Процесс распространения упругих волн в грунтовом массиве является затухающим и оценивается коэффициентом относительной диссипации.

2 P ×sin t

r

Zr

Z0

r0

r

z

Рис. 8.5. Схема распространения колебаний в грунтовом массиве: 1 – источник колебаний; 2 – объект, на который оказывается влияние динамического воздействия; Z 0, Zr – амплитуды колебаний; r 0, r – радиусы зон распространения колебаний.

Практически колебания в грунтовом массиве могут оказывать влияние на объекты строительства, расположенные на расстоянии десятков и сотен метров от источника колебаний, например, от железнодорожной магистрали. Затухание амплитуды поверхностной волны в массиве может быть оценено по формуле:

Z r = Z 0×

r 0 ×

r

e -  0 (r - r 0),

(8.9)

где Zr, Z0 – амплитуда колебаний на расстоянии r и r0 от источника колебаний (центра фундамента); r0 - радиус источника колебаний (фундамента); 0 – коэффициент поглощения энергии волн (м-1).

Величина коэффициента поглощения энергии волн зависит от вида грунтов, слагающих массив, и принимается равной: для слабых пылевато-

a) 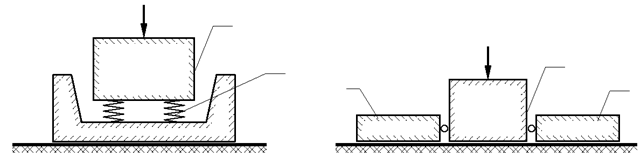P ×sin t 1 б)

P ×sin t

2 1

3 3

Рис. 8.6. Принципиальные схемы виброгасителей колебаний: а - с использованием амортизаторов; б – с использованием присоединённых масс; 1 – фундамент с динамической нагрузкой; 2 – пружины – амортизаторы; 3 – шарнирно - присоединённые массы.

глинистых грунтов 0,03–0,04; для песков 0,04–0,06; для плотных глин 0,06– 0,1.

Виброгасители колебаний. Предназначены для изменения частотных характеристик системы “основание – фундамент – верхнее строение” с целью уменьшения амплитуд вынужденных колебаний фундамента. Как уже было показано выше, динамический коэффициент колебательного процесса уменьшается при удалении частоты собственных колебаний конструктивной системы от частоты вынужденных колебаний (динамической нагрузки). На практике это достигается применением виброгасителей колебаний. Различают два основных типа виброгасителей: виброгасители с присоединенными массами (рис. 8.6 б); виброгасители с пружинами – амортизаторами (рис. 8.6 а). Шарнирно присоединенные массы значительно увеличивают площадь подошвы фундамента и незначительно увеличивают его массу. В соответствии с формулами (8.5) это приводит к уменьшению амплитуды колебаний фундамента. Жесткостные характеристики пружин – амортизаторов подбираются таким образом, чтобы исключить явление резонанса при работе динамической машины.

Дата добавления: 2014-01-07