Закон уплотнения Терцаги

Закон уплотнения является одним из основных законов механики грунтов, основанным на допущении о том, что деформации грунта происходят, в основном, за счет изменения его пористости. В качестве предварительных замечаний отметим следующее. Грунт существенно отличается от таких строительных материалов как сталь, бетон и т.п. Крупнообломочные и песчаные грунты не обладают связностью. Связные пылевато-глинистые грунты имеют очень низкую прочность при одноосном сжатии. Все это создает большие проблемы при экспериментальном определении прочностных и деформационных характеристик грунтов. Поскольку не представляется возможным испытать грунт при одноосном напряженном состоянии (растяжение, сжатие), как это принято для большинства строительных материалов, для испытания грунтов используют схемы со сложным напряженным состоянием (см. курс "Инженерные изыскания в строительстве"). Одной из таких схем является схема осесимметричного компрессионного сжатия (рис. 1.3). Граничными условиями в такой схеме являются нулевые значения поперечных деформаций. Возникающие на боковых поверхностях цилиндрического образца давления не измеряются, а оцениваются теоретически. При этом касательные напряжения на этих поверхностях предполагаются равными нулю, в связи с чем вертикальное и боковое давления – суть главные напряжения. Ниже приводятся теоретические выкладки, связанные с приложениями закона уплотнения Терцаги, простейший вид которого уже рассматривался в курсе "Инженерные изыскания в строительстве".

Рис. 1.3. Напряженное состояние грунта в виде осе­симметричного компрессион­ного сжатия: 1 – цилиндриче­ский образец грунта; 2 – жесткое кольцо с безфрикционной внутренней поверхностью; р – вертикальное давление; р_W – давление в поровой воде; А_g – площадь поперечного сечения грунта; h₀, h_i – соответственно высота ненагруженного и нагружен­ного образца грунта; s_x, s_y, s_z, t_zx, t_zy – компоненты тензора напряжений; e_x, e_y – компоненты тензора деформаций

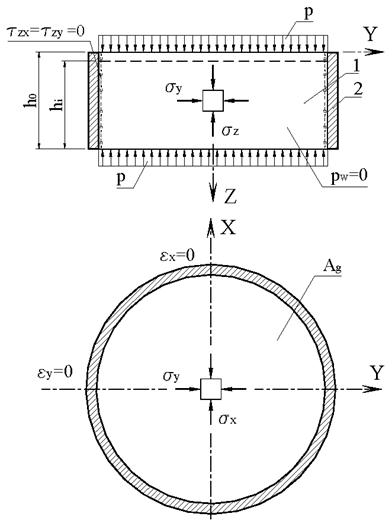
5.1. Определение коэффициента бокового давления при осесиммет­ричном компрессионном сжатии грунта. Примем зависимости между деформациями и напряжениями в грунте в форме закона Гука:

;

;

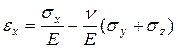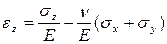. (1.5)

Введем понятие коэффициента бокового давления в виде отношения бокового давления к нормальному. Тогда, с учетом осевой симметрии,

s_x = s_y = x × s_z,

где x – коэффициент бокового давления.

Граничные условия при осесимметричном компрессионном сжатии имеют вид: e_x = e_y = 0. Воспользуемся одним из граничных условий и выразим коэффициент бокового давления через коэффициент Пуассона, значение которого для различных видов грунтов содержатся в справочных данных. Преобразования будут иметь вид:

;
;
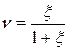. (1.6)

В соответствии с полученными выражениями коэффициент бокового давления тем выше, чем более пластичным является грунт, и для состояния текучести, когда n ® 0,5, принимает значения, близкие к единице.

5.2. Зависимость между осевой деформацией и вертикальным давлением при осесимметричном компрессионном сжатии. Эту зависимость получим путем преобразования выражения для осевой деформации в соответствии с законом Гука (1.5) с учетом полученной в п. 5.1 зависимости между коэффициентом бокового давления и коэффициентом Пуассона:

;
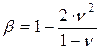. (1.7)

5.3. Зависимость между осевой деформацией и изменением коэффициента пористости при осесимметричном компрессионном сжатии. При компрессионном сжатии образца грунта измеряются изменения его высоты Dh_i = h₀ – h_i. При этом начальной высоте образца грунта h₀ соответствует коэффициент пористости e₀, а измененной высоте образца h_i – измененный коэффициент пористости e_i. Измененный коэффициент пористости e_i вычисляется через измеряемые в опыте величины в соответствии с выражением:

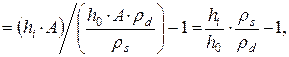
где V_n,i и V_i – объем пор в грунте и объем грунта при высоте образца h_i;
A – площадь поперечного сечения образца грунта.

Изменение коэффициента пористости, вызванное нагружением грунта в условиях компрессионного сжатия, вычисляется в функции от осевой деформации по следующей зависимости:

Из полученного выражения находим зависимость осевой деформации от изменения коэффициента пористости в условиях компрессионного сжатия:

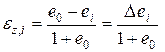. (1.8)

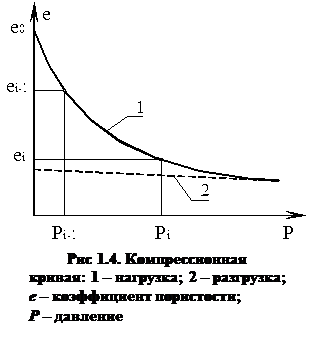5.4. Закон уплотнения. Зависимость изменения коэффициента пористости от вертикального давления при компрессионном сжатии грунта изображают графиком (рис. 1.4), который называют компрессионной кривой. Начало графика (на рис. 1.4 не показано) обычно изображают горизонтальной линией, параллельной оси давлений. Искривление графика начинается с момента разрушения структурных связей или с момента исчерпания структурной прочности грунта, что одно и то же. После этого деформации грунта происходят исключительно за счет его уплотнения, т.е. изменения пористости. В опыте на компрессион­ное сжатие должно, как правило, отсутствовать поровое давление, что достигается применением открытой, по отношению к фильтрации поровой воды, схемы испытания (испытание по дренированно-консолидированной схеме). Присутствие порового давления в опыте может существенно исказить результаты испытаний (занизить значение коэффициента сжимаемости и завысить значение модуля деформации). Закон уплотнения грунта формулируется следующим образом: изменение коэффициента пористости при достаточно малом изменении давления пропорционально изменению давления. Применительно к графику на рис. 1.4 закон уплотнения выражается такой зависимостью:

e_i-1 – e_i = m₀ × (p_i – p_i-1), (1.9)

где m₀ – коэффициент сжимаемости грунта (м²/кН).

В дифференциальной форме закон уплотнения записывается в виде выражения:

de = - m₀ × dp, (1.10)

где знак «минус» указывает на то, что увеличению давления соответствует уменьшение коэффициента пористости.

Закон уплотнения в форме (1.10) может использоваться только при анализе напряженных состояний грунтового массива, близких к компрессионному сжатию. Характеристикой сжимаемости грунта при этом виде напряженного состояния является коэффициент сжимаемости m₀. Для общего случая напряженного состояния грунта закон уплотнения выражают в форме зависимости осевой деформации от давления:

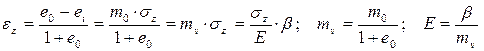, (1.11)

где m_v – коэффициент относительной сжимаемости грунта (м²/кН);
Е – модуль деформации грунта (кН/м²);
b – коэффициент вида напряженного состояния в опыте по определению модуля деформации грунта (при определении модуля деформации в опыте при компрессионном сжатии грунта b = 1 - (2 ×n ²) / (1 -n), см. (1.7)).

Закон уплотнения в форме (1.11) позволяет вычислять осевую деформацию при компрессионном сжатии с помощью коэффициента относительной сжимаемости грунта m_v (сравните, изменение коэффициента пористости в этом случае вычисляется с помощью коэффициента сжимаемости m₀). В общем случае напряженного состояния осевая деформация вычисляется с помощью модуля деформации грунта Е. При этом закону уплотнения в форме (1.11) можно дать такую формулировку: модуль деформации грунта обратно пропорционален коэффициенту относительной сжимаемости грунта и прямо пропорционален некоторой функции коэффициента Пуассона, учитывающей вид напряженного состояния при компрессионном сжатии.

Наряду с рассмотренными выше лабораторными методами, для определения модуля деформации грунтов широко применяются полевые методы. Наиболее распространенным является метод испытания грунтов жестким круглым штампом площадью 5000 см². По результатам испытаний строят график зависимости осадок штампа от средних давлений по его подошве (рис. 1.5).

S

Модуль деформации грунта вычисляют по формуле:

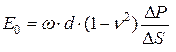, (1.12)

где E₀ – модуль общей деформации грунта (кН/м²);
w – коэффициент, принимаемый для круглых жестких штампов 0,8;
D Р – приращение среднего давления по подошве штампа (кПа);
D S – приращение осадки штампа при изменении давления на D Р (м);
d – диаметр штампа (м).

Установлено, что модули деформации грунта, определенные в лабораторных (1.11) и полевых (1.12) условиях, могут существенно отличаться. При этом, чем меньше коэффициент пористости грунта, тем эта разница больше. В связи с этим модуль деформации, определенный в лабораторных условиях (1.11), умножают на поправочный коэффициент И.А. Агишева. Этот коэффициент изменяется от 2 для рыхлых грунтов (e = 1,6) до 7,5 для плотных грунтов (e = 0,2). Для суглинков Донбасса он изменяется от 3 до 6. Модуль деформации принимает значения от 5 МПа для слабых грунтов до 30 МПа для прочных грунтов. Модуль деформации скальных грунтов составляет 100 МПа и выше.

Таким образом, деформационными характеристиками грунта являются: модуль деформации E; коэффициент поперечной деформации (Пуассона) n; коэффициент сжимаемости m₀; коэффициент относительной сжимаемости m_v.

Дата добавления: 2014-01-07