Метод анализа иерархий

Графоаналитический метод

Если в методах, расмотреных выше, решение принималось на основе расчетов, то при применении графоаналитических методов для выбора управленческого решения используется изображение. Популярен метод, названный “Полигон альтернатив”. “Полигон” представляет собой наглядную диаграмму, построенную в полярных координатах. Оси, на которые наносятся значения критериев, направлены по радиусам от центра окружности к периферии. Число осей соответствует числу выбранных критериев.

На оси наносятся оценочные шкалы для каждого критерия. Предварительно определяют, где должны находиться наилучшие значения - ближе к центру или дальше от него. Это условие должно быть одинаковым для всех критериев.

Для каждой альтернативы на диаграмме отмечают ее оценки по каждому критерию. Полученные точки соединяют замкнутой ломанной линией - полигоном. На полярной диаграмме образуются в общем случае неправильные n - угольники, где n - число критериев.

Правило оценки этим методом гласит: если наилучшее значение критерия расположено дальше от центра, то оптимальному решению соответствует многоугольник, имеющий максимальную площадь, и наоборот.

Вполне эффективным методом выбора на основе нескольких критериев является метод анализа иерархий (МАИ), разработанный Т. Саати.

Суть МАИ - декомпозиция проблемы на части (элементы), которые оцениваются в шкале МАИ в виде суждений ЛПР (экспертов). А затем, после обработки совокупности суждений методом матричной алгебры, формируются конечные оценки. При этом определяется относительная степень взаимного влияния в иерархии.

Цель, факторы показательного оценивания и альтернативы образуют иерархическую структуру (рис. 5.1.).

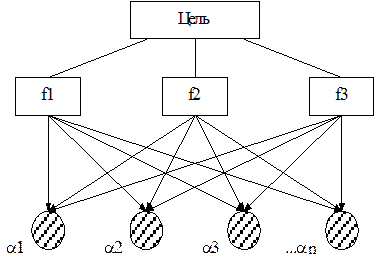
Рис. 5.1. Дерево целей МАИ: f1,f2,f3 - факторы (показатели), характеризующие альтернативы; a1,a2,...an - множество альтернатив

Рассмотрение этой схемы (рис. 5.1.) позволяет сформулировать ряд положений, отражающих сущность метода «анализа иерархий».

1. Число уровней иерархии, описывающих конкретную прикладную задачу, может быть различно и зависит от специфики задачи. Каждый элемент верхнего уровня является «направляющим» для элементов нижнего уровня иерархии. Это означает, что важность (весовой коэффициент факторов описываемой альтернативы) рассматривается относительно цели выбора альтернатив. Поэтому при бинарном сравнении факторов каждый из них оценивается относительно поставленной цели выбора и соответственно определяет уровни взаимного предпочтения.

2. Попарные сравнения факторов осуществляются в терминах доминирования одного из элементов над другим. Эти суждения в шкале МАИ выражаются в целых числах. Если элемент А доминирует над элементом В, то клетка квадратичной матрицы, соответствующей строке А и столбцу В, заполняется целым числом, а клетка, соответствующая строке B и столбцу A, заполняется обратным к нему числом. Если A и B эквивалентны, то в обе позиции записывается 1.

3. Для получения каждой матрицы требуется n×(n-1)/2 суждений, где n – число факторов, если сравнение проводится среди них, или n – число альтернатив, если они сравниваются по каждому фактору.

4. При бинарном сравнении альтернатив, в особенности при близких оценках их показателей, возможны случаи нарушения требований транзитивности или других ошибок в суждениях, поэтому МАИ предусматривает специальный механизм определения согласованности оценок.

Обработка результатов осуществляется на базе методов матричного анализа с использованием ряда специальных процедур оценки предпочтений ЛПР на основании шкалы МАИ (табл. 5.2.).

Таблица 5.2.

Шкала отношений МАИ

Степень важности	Определение	Пояснение
	Одинаковая значимость	Два действия вносят одинаковый вклад в достижение цели
	Некоторое преобладание значимости одного действия (показателя фактора) перед другим, слабая зависимость	Опыт и суждения дают легкое предпочтение одному действию перед другим
	Существенная или сильная значимость	Опыт и суждения дают сильное предпочтение одному действию перед другим
	Очень сильная или очевидная значимость	Предпочтение одного действия над другим очень сильно, его превосходство практически явно
	Абсолютная значимость	Свидетельство в пользу предпочтения одного действия другому в высшей степени убедительно
2,4,6,8	Промежуточные значения между соседними значениями шкалы	Ситуация, когда необходимо компромиссное решение
Обратные величины приведенных чисел	Если действию i при сравнении с j присваивается одно из приведенных выше чисел, то действию j по сравнению с i присваивается обратное значение	Если над диагональю стоит целое число, то под диагональю его - обратное значение
Рациональное значение	Отношение, возникающее в заданной шкале	Если постулировать согласованность, то для получения матрицы требуется n- числовых значений

В общем случае, когда матрица М[n] содержит элементы согласованности суждений, указанные способы дают различные результаты векторов приоритетов. Расчет показателей согласованности выполняется следующим образом.

Определяется приближенная оценка главного собственного значения матрицы суждений. Для этого суммируется столбец суждений, а затем сумма первого столбца умножается на величину первой компоненты нормализованного вектора приоритетов, сумма второго столбца – на вторую компоненту и т.д. Затем полученные числа суммируются. Таким образом получаем l_max, которая называется оценкой максимума или главного значения матрицы М. Это приближение используется для оценки согласованности суждений эксперта. Чем ближе l_max к n, тем более согласованным является представление в матрице М[n] суждений. Отклонения от согласованности могут быть выражены величиной, которая называется индексом согласованности (ИС).

.

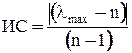При оценивании величины порога несогласованности суждений для матриц размером от 1 до 15 методом имитационного моделирования получены оценки случайного индекса (СИ). СИ является индексом согласованности для сгенерированной случайным образом (по шкале от 1 до 9) положительной обратно симметричной матрицы. В табл. 5.3. приведены средние (модельные) значения СИ для матриц порядка n = 1÷15.

Таблица 5.3.

Индексы согласованности

n
СИ			0,58	0,9	1,12	1,24	1,32	1,41	1,45	1,49	1,51	1.48	1,56	1,57	1,59

Отношение ИС к среднему СИ для матрицы суждений того же порядка Саати называет отношением согласованности (ОС):

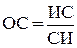при n = const,

где n - количество элементов матрицы.

Значение ОС £ 0,10 считается приемлемым порогом допустимой согласованности суждений. Если значение ОС > 0,10, данные в матрице суждений необходимо уточнить.

Обобщенные веса (или приоритетность объекта при их выборе) определяются суммой произведений локальных приоритетов каждого объекта по каждому критерию на значимость этого критерия.

5.4. Методы «стоимость - эффективность», «стоимость - выгода»

При выборе решений могут применяться экономические критерии вида “стоимость - эффективность” и “стоимость - выгода”. В отличие от методов, рассмотренных выше, когда решение принималось по множеству критериев,- это двухкритериальные методы.

Проблема формулировки количественного критерия в условиях подхода к оцениваемым системам как многоцелевым является исключительно сложной и зачастую не может быть решена на основе строго формальных обоснований и методов расчета. Ее решение осуществляется различными способами. При первом способе на каждой итерации системного исследования характер критерия эффективности и его численное значение могут уточняться и изменяться. Второй способ состоит в том, чтобы разработать и предложить руководству несколько курсов действий, каждый из которых является наиболее предпочтительным при разных предпосылках относительно приоритета целей. При третьем способе применяются нестрогие оценочные критерии выбора альтернатив, которые косвенно отображают действительные объективно обусловленные цели системы. Важное значение при этом имеет тот факт, что для выбора наилучших решений достаточно иметь критерий оценки сравнительной ценности отдельных альтернатив и совсем не обязательно давать адекватное абсолютное измерение величины стоимости, полезности или эффективности.

Математическим методом анализа в исследованиях первых двух способов является построение «кривых безразличия» (изоквант). Кривая безразличия—это область, которую составляет совокупность вариантов, равноценных по эффективности, но различных с точки зрения комбинации факторов, влияющих на эффективность, а отсюда и с точки зрения стоимости. Для каждого уровня эффективности строится соответствующая кривая безразличия, такого рода кривые совмещаются с линией или поверхностью, отражающей зависимость суммы денежных средств от комбинации факторов системы и отыскивается точка, обеспечивающая максимальную эффективность на единицу денежных средств.

Третий способ исследований осуществляется в более сложных случаях, когда альтернативные проекты прямо не сопоставимы ни с точки зрения стоимости, ни с точки зрения эффективности. При оценке такого рода мероприятий критерием сравнения альтернатив является относительный показатель: эффективность на единицу денежных затрат или стоимость на единицу эффективности.

Метод “стоимость—эффективность” в наиболее развернутой форме представляет собой обстоятельное и дорогостоящее исследование, осуществление которого целесообразно прежде всего при разработке крупных мероприятий, связанных со значительными единовременными и текущими затратами. Экономическая оценка систем основывается на трех ключевых параметрах: стоимость, эффективность и время.

Матрица стоимости представляет собой прямоугольную таблицу, на пересечении строчек и столбцов которой указываются затраты в денежном выражении по каждому из системных элементов (строки матрицы) и по категориям или элементам затрат (столбцы матрицы). Заполнение матрицы стоимости - это процесс построения численной модели стоимости, который осуществляется специалистами по анализу стоимости на основе нормативных и математико-статистических методов.

Для построения матрицы стоимости необходим прогноз стоимостных оценок С_ij, где i — индекс системного элемента, j — индекс категории стоимости. Это составляет особую сложность, особенно для проектов и программ с высоким удельным весом уникальных элементов.

При построении прогностических оценок стоимости применяются два основных метода: экспертно-аналитический и статистический. Экспертно-аналитический метод заключается в разработке детализированных спецификаций и списков оборудования, материалов и рабочей силы для будущей системы и в подробной оценке ее стоимости на основе этой спецификации. Суть статистического подхода - построение соотношений для оценки стоимости, в которых корреляционными методами (различными модификациями метода наименьших квадратов, методом максимального правдоподобия или итеративными методами) на базе достаточно большого объема данных строятся зависимости между стоимостью системных элементов и наиболее важными параметрами этих элементов.

Матрица эффективности по подлежащему имеет перечень тех же системных элементов, как и матрица стоимости, что обеспечивает их сопоставимость.

Основные принципы оценки затрат при осуществлении анализа “стоимость—выгода” совпадают с аналогичным подходом к экономической оценке затрат в методе “стоимость—эффективность”. Специфической стадией анализа “стоимость—выгода” является денежная оценка общественных выгод в результате осуществления проектов и программ.

Выбор наилучших решений на основе критерия “стоимость—выгода” базируется, как и в анализе “стоимость—эффективность”, на идеях предельного анализа. Исходным является положение, вытекающее из математической теории оптимизации и состоящее в том, что ограниченные ресурсы (в частности, денежные средства) будут в целом использованы оптимально, если по каждой из программ уравновешиваются маргинальные (т. е. предельные, приростные) затраты и предельная выгода.

Часто, используя этот метод, находят соотношение эффективности (выгодности) Вк и стоимости Ск, характеризующую ожидаемое значение выгоды на единицу затрат. Далее, упорядочив проекты по убыванию значения отношения Вк/Ск, рассматриваемые проекты ранжируют по степени предпочтительности, имея в виду, что наиболее предпочтительным проектом является проект с наибольшей ожидаемой эффективностью, получаемой на единицу затрат.

Для того, чтобы сформировать портфель проектов, обладающих максимальной эффективностью, необходимо последовательно включать в такой перечень проекты по убыванию отношения Вк/Ск до тех пор, пока не будет исчерпан выделенный на финансирование проектов объем средств С*.

Если проекты, включенные в перечень согласно изложенному выше алгоритму, полностью исчерпывают С*, то лицо, принимающее решение, получает оптимальное решение задачи распределения ресурсов.

Дата добавления: 2014-01-07