Управленческих задач

Метод линейного программирования в решении

Под линейным программированием понимается линейное планирование, т.е. получение оптимального плана – решения в задачах с линейной структурой. Обычно его используют специалисты штабных подразделений для разрешения производственных трудностей. Типичными примерами применения модели линейного программирования являются следующие:

· укрупненное планирование производства (составление графиков производства, минимизирующих общие издержки в связи с изменением ставки процента);

· планирование ассортимента изделий (определение оптимальной структуры производства продуктов питания для человека);

· маршрутизация производства изделий (определение оптимального технологического маршрута изготовления изделия);

· регулирование запасов (определение оптимального сочетания продуктов на складе);

· календарное планирование производства (составление календарных планов, минимизирующих издержки с учетом расходов на содержание запасов, оплату сверхурочной работы и заказов на стороне);

· планирование распределения продукции и др.

В основу универсального метода решения задач линейного программирования положен симплекс-метод.

При применении симплекс-метода условие исходной задачи принимает вид:

¦ = c₁x₁ + c₂x₂ + …+ c_nx_n ® max

a₁₁x₁ + a₁₂x₂ + …+ a_1nx_n + у₁ £ b₁

a₂₁x₁ + a₂₂x₂ + …+ a_2nx_n + у₂ £ b₂

…………………………..

a_m1x₁ + a_m2x₂ + …+ a_mnx_n + у_m £ b_m

x₁ ³ 0, x₂ ³ 0,…, x_n ³ 0, у_m ³ 0

Эту постановку можно представить в виде таблицы – первой таблицы симплекс-метода (табл.6.1.).

Таблица 6.1.

Первая симплекс-таблица

Базис	Свободные члены	Свободные переменные
x1	x2	…	хn
y1	b1	a11	a12	…	a1n
y2	b2	a21	a22		a2n
…	…	…	…	…	…
ym	bm	am1	am2		amn
Индексная строка		-c1	-c2	…	-cn

Для составления симплекс таблиц можно применять определение правила.

1. Для первой таблицы:

а) в первый столбец записывают y_m - базисные переменные, которые находятся в уравнениях слева;

б) свободные переменные a_mn, выносят в верхнюю строку таблицы;

в) в остальные столбцы записывают коэффициенты перед свободными переменными.

2. Для последующих таблиц:

а) выбирается наименьший отрицательный элемент в индексной строке при отыскании максимума, но наибольший положительный – при отыскании минимума, исключая вектор свободных членов;

б) этот элемент определяет ключевой вектор-столбец, и он вводится в базис;

в) компоненты вектора свободных членов делятся на положительные элементы ключевого столбца;

г) из полученных отношений выбирается наименьшее;

д) вектор-строка, содержащая наименьшее положительное частное, - ключевая и выводится из базиса;

е) на пересечении ключевых строк и столбца находится разрешающий элемент;

ж) преобразование матрицы:

· каждый элемент ключевой строки делится на разрешающий

элемент. Полученные частные являются элементами ключевой строки следующей таблицы;

· ключевой столбец в новой таблице – нули, за исключением

разрешающего элемента;

· остальные элементы новой таблицы рассчитываются по схеме:

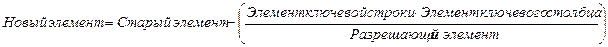
· если нулевая строка (столбец) содержит нуль, то соответствующий

столбец (строка) в новой таблице не изменится.

3. Пункты а) – ж) повторяются до тех пор, пока в индексной строке не останется ни одного отрицательного элемента при отыскании максимума (но ни одного положительно при отыскании минимума).

Недостатком метода линейного программирования является его узость, так как он не учитывает все факторы, необходимые для принятия решений. Например, полученный план производства может не учитывать фактор «рыночный спрос». Поэтому результаты, полученные с помощью такой экономико-математической модели, могут нести рекомендательный характер при принятии управленческого решения.

Дата добавления: 2014-01-07