Теория полезности и ее использование для поиска решения

Полезностью называют величину, которую в процессе выбора максимизирует личность с рациональным экономическим мышлением. Можно сказать, что полезность - это воображаемая мера психологической и потребительской ценности различных благ.

С содержательной точки зрения делается предположение, что человек как бы взвешивает на некоторых «внутренних весах» различные альтернативы и выбирает из них ту, полезность которой больше.

Задачи принятия решений с рассмотрением полезностей и вероятностей событий были первыми, которые привлекли внимание исследователей. Постановка таких задач обычно заключается в следующем. Человек выбирает какие-то действия в среде, где на получаемый результат (исход) действия влияют случайные события, неподвластные ему. Но имея некоторые знания о вероятностях этих событий человек может рассчитать наиболее выгодную совокупность и очередность своих действий.

Основная трудность принятия решений в условиях неопределенности сводится к невозможности расчета достоверности прогноза или оценки вероятности наступления конкретных событий во внешней среде. Эта особенность ситуации исключает применение математических моделей, характерных для условий определенности. Выбор альтернативного решения при этом осуществляется с помощью количественных и качественных методов. В основе условно количественных методов лежит, во -первых, «теория полезности», во-вторых, приведение ситуации неопределенности к ситуациям риска и применения адекватных способов принятия решения. К качественным методам относится использование «байесовского подхода», основанного на опыте, знаниях, интуиции ЛПР.

В теории принятия решений важное место занимают положения теории полезности. Следует отметить определенную условность в названии теории, не имеющей ничего общего с бытовым значением термина «полезность». Упомянутый однажды, он закрепился в литературе, хотя и не признается специалистами удачным.

Основополагающим в теории полезности является линия поведения ЛПР, его субъективная оценка вероятности наступления события и его полезности. Полезность в данной теории используется для замены количественного выражения ожидаемого результата той или иной стратегии, поскольку его нельзя предугадать. Термин «полезность» воспринимается как важность конечного варианта решений, которую можно оценить формально, например, как оценку приоритетов альтернатив решений.

Потери или выигрыш могут оцениваться как количественно (например, через затраты разного вида ресурсов), так и качественно (утрата авторитета, престижа, имиджа организации, потери времени, ухудшение социально-психологического климата в коллективе и др.).

Полезность выступает в качестве приведенного показателя, обобщенно выражающего потери или выигрыш, когда все ценности приведены к одной шкале. Для определенного события она будет соответствовать какой-то точке на этой шкале. Причем шкала полезности определяется логикой руководителя, его выводами и предпочтительностью. От руководителя зависит выбираемый критерий оценки решения. Предварительно строится матрица (таблица) решений на основе логических рассуждений.

Полезность измеряется в произвольных единицах, называемых единицами полезности. Они могут быть связаны с денежными единицами и означать для ЛПР величину полезности. В условиях риска ЛПР выбирает вариант, максимизирующий величину полезности.

Итак, теория полезности строится на предположении, что некоторое число V(P), выражает полезность события, которое может произойти. Если, например, событие Р₁ может принести прибыль в размере 200 тыс. руб., а событие Р₂ - 100 тыс. руб., то VР₁ > VР₂.

Сущность теории полезности покажем на простейшем бытовом примере. Уходя на работу мы задумываемся: брать с собой зонт или нет? Возможность дождя от нас не зависит - это объективные условия внешней среды. Возможны два варианты решений: взять зонт (а₁) и не брать зонт (а₂). На наш выбор по влияют внешние условия: пойдет дождь (у ₁) или не пойдет (у₂) Допустим, мы считаем, что вероятность дождя рУ₁ = 0,5, тогда вероятность хорошей погоды 1-0,5 = 0,5 (рУ₂).

Далее необходимо дать оценку потерь (неудобств), которые можно иметь по вариантам возможных решений и влияния погодных условий. Эта оценка у разных людей может быть различной (в данном случае в зависимости от отношения индивидуума к дождю и сохранению своей одежды). Но у большинства людей существует какое-то среднее мнение. При решении сложных проблем на данном этапе может быть использован метод экспертных оценок возможных потерь.

В нашем случае примем следующую оценку. По варианту а₁ (взять зонт) оценка будет равна 1 (а₁₁), если дождь пойдет, и 2 (а₁₂), если дождя не будет. Это означает, что во время кратковременного пребывания на улице дождя не будет и неудобство носить зонт оценивается единицей, а если вообще дождь не пойдет, то неудобство увеличится вдвое.

По варианту а₂ соответственно возможны два события: дождь пойдет а₂₁ - оценивается числом 6 (опасность испортить одежду, прическу во время дождя при отсутствии зонта) и а₂₂ -0 - при отсутствии зонта и дождя.

Составим таблицу потерь на основе рассуждений и принятых оценок.

Таблица 8. 2.

Линия поведения	Объективные условия
дождь (у1)	нет дождя (у2)
взять зонт (а1)	1 (а11)	2 (а12)
не брать зонт (а2)	6 (а21)	0 (а22)

Далее определим математическое ожидание потерь при выборе альтернативных линий поведения. Так как математическое ожидание (Е) случайной величины равно Е_х = Spixi, то в нашем случае, при вероятности р = 0,5, для а₁ и а₂ оно будет равно соответственно:

Ea ₁ = 0,5*1 +0,5*2 = 1,5

Еа ₂ = 0,5*6 + 0,5*0 = 3,0

Чтобы минимизировать возможные потери, в нашем примере необходимо остановить выбор на линии поведения а₁,то есть взять зонт.

В развитие данной теории предлагается при выборе решений исходить из максимума ожидаемой полезности, используя для расчета формулу:

П = (Bу*Оy)-(Bh*Пi), где П - ожидаемая полезность, Ву - вероятность успеха, Оу -оценка удачи, Вн - вероятность неудачи, Пн - потери от неудачи.

Формула логична и доступна. Часто ЛПР интуитивно в ходе принятия решений оценивают положительные и отрицательные исходы. Трудность состоит в точности определения вероятности объема удач и потерь. При этом вероятность может быть установлена на основе экспертных оценок, проведения специальных исследований, логических умозаключений. Оценка величины удач или потерь должна подкрепляться дополнительными расчетами.

Использование теории полезности не гарантирует высокой точности результатов расчета ожидаемой полезности. Однако оно дает возможность сравнить альтернативы по критерию полезности и исключить те из них, которые потенциально связаны со значительным ущербом. Кроме того, достоинством данной теории является учет количественных и качественных аспектов вариантов решений, таких как человеческий фактор, а также случайностей, способных оказать негативное влияние.

Кроме классической теории полезности при принятии решений используют также многокритериальную теорию полезности ((MAUT).

Научное направление MAUT (Multi-Attribute Utility Theory) отличают следующие особенности:

1)строится функция полезности, имеющая аксиоматическое обоснование;

2) некоторые условия, определяющие форму этой функции, подвергаются проверке в диалоге с ЛПР;

3) решается обычно задача из второй группы, а полученные результаты используются для оценки заданных альтернатив.

Логика решения задачи в MAUT такова:

Составляется перечень критериев; строится функция полезности по каждому из критериев; проверяются условия, определяющие вид общей функции полезности; находится зависимость между оценками альтернатив по критериям и общим качеством альтернативы (многокритериальная функция полезности); оцениваются имеющиеся альтернативы и выбирается наилучшая.

Теория MAUT имеет аксиоматическое обоснование. Это означает, что выдвигаются некоторые условия (аксиомы), которым должна удовлетворять функция полезности ЛПР. В случае, если условия удовлетворяются, дается математическое доказательство существования функции полезности в том или ином виде. В MAUT эти условия можно разделить на две группы. Первая группа — аксиомы общего характера, идентичные тем, которые использовались в теории полезности.

1. Аксиома, утверждающая, что может быть установлено отношение между полезностями любых альтернатив: либо одна из них превосходит другую, либо они равны.

2. Аксиома транзитивности: из превосходства полезности альтернативы А над полезностью альтернативы В и превосходства полезности В над полезностью С следует превосходство полезности альтернативы А над полезностью альтернативы С.

3. Для соотношений между полезностями альтернатив А, В, С, имеющими вид U(A)>U(B)>U(C) можно найти числа а, р, которые меньше 1 и больше 0, так что:

aU(A)+(l-a)U(C)=U(B),

U(A)(l-p)+pU(B)>U(B).

Аксиома 3 основана на предположении, что функция полезности непрерывна и можно использовать любые малые части полезности альтернатив.

Вторая группа условий специфична для MAUT. Они называются аксиомами (условиями) независимости, позволяющими утверждать, что некоторые взаимоотношения между оценками альтернатив по критериям не зависят от значений по другим критериям.

Приведем несколько условий независимости.

1. Независимость по разности. Предпочтения между двумя альтернативами, отличающимися лишь оценками по порядковой шкале одного критерия С₁, не зависят от одинаковых (фиксированных) оценок по другим критериям С₂,..., C_N. На первый взгляд, это условие кажется естественным и очевидным. Но возможны случаи, когда оно не выполняется. Пример. Надо выбрать автомобиль. При примерно одинаковой цене ЛПР предпочитает большую по размеру машину. Однако его предпочтение меняется на обратное, когда он узнает, что у машины не гидравлическая, а механическая коробка передач, что усложняет управление.

2. Независимость по полезности. Критерий С₁ называется независимым по полезности от критериев С₂,..., C_n, если порядок предпочтений лотерей, в которых меняются лишь уровни критерия С₁, не зависит от фиксированных значений по другим критериям. Такие лотереи используются при построении функций полезности по отдельным критериям.

3. Независимости по предпочтению являются одним из наиболее важных и часто используемых условий. Два критерия C₁ и С₂ независимы по предпочтению от других критериев С₃,...,С_n, если предпочтения между альтернативами, различающимися лишь оценками по С₁ , С₂, не зависят от фиксированных значений по другим критериям.

Если аксиомы первой группы и некоторые из условий независимости выполнены, то из этого следует строгий вывод о существовании многокритериальной функции полезности в определенном виде.

В качестве примера приведем широко известную теорему Р. Кини. Если условия независимости по полезности и независимости по предпочтению выполнены, то функция полезности является аддитивной

U(x) = Sw_iU_i(x) при Sw_i=1
либо мультипликативной

l + kU(x) = P [1 + kw_iU_i,(x)] при Sw_i ¹1,

где U, U_i - функции полезности, изменяющиеся от 0 до 1; w_i -коэффициенты важности (веса) критериев, причем 0< w_i <1; коэффициент k>-1. Таким образом, многокритериальную функцию полезности можно определить, если известны значения коэффициентов w_i,k, а также однокритериальные функции полезности U_i (x).

Пример выбора места постройки аэропорта. В условном городе возникла необходимость в постройке нового аэропорта. Экспертным путем были выбраны три основных критерия для оценки вариантов расположения аэропорта:

· стоимость постройки;

· расстояние от города;

· минимальное шумовое воздействие.

Все критерии противоречивы. Постройка аэропорта на большом расстоянии от города потребует меньших затрат, но время поездки будет больше. Противоречивы и критерии «расстояние от города» и число людей, подвергающихся «шумовым воздействиям». Для нахождения компромисса между критериями и выбора оптимального решения можно применить многокритериальную теорию полезности путем построения модели, описывающей предпочтения ЛПР.

Предположим, что после рассмотрения вариантов разброс оценок по критериям может быть представлен в таблице 8.3.

Таблица 8.3.

Разброс оценок вариантов постройки аэропорта

Критерий	Наихудшее значение	Наилучшее значение
(C1) Стоимость постройки аэропорта	$ 200 млн	$ 100 млн
(С2) Время поездки от центра города	90 мин	40 мин
(Сз) Количество людей, подвергающихся шумовым воздействиям	50 тыс.	5 тыс.

Зная диапазон изменения оценок по каждому критерию, построим функцию, определяющую полезность для ЛПР каждой оценки из этого диапазона. Максимальное значение этой функции примем равным единице, а минимальное - нулю.

На рис. 8.1. приведен пример построения функции полезности ЛПР для критерия «Стоимость постройки аэропорта».

UC₁

UC₁

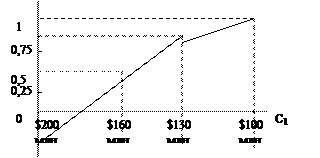Рис. 8.1. Функция полезности для критерия С₁

Первоначально известны две точки функции полезности: U($100 млн)=1, U($200 млн)=О. Для нахождения промежуточных точек используется метод лотереи. В лотерее 1 на рис. 9.2. (слева) перед ЛПР ставится следующая задача: «Определите эквивалент определенности для лотереи, имеющей с равными вероятностями (р=0,5) минимальную и максимальную стоимости постройки». ЛПР предъявляют ряд значений (например, $120 млн, $130 млн и т. д.) и спрашивают: выше или ниже данного значения находится, по его мнению, эквивалент определенности. Предположим, что ЛПР остановился на значении $160 млн. Тогда делается вывод, что U=0,5 соответствует $160 млн. Аналогично определяются другие значения функции полезности. Так, правая лотерея на рис. 8.2. позволяет определить точку U($130 млн)=0,85.

Идентичным образом строятся функции полезности для каждого из критериев.

Рис. 8. 2. Типовые лотереи, используемые при построении функции

полезности по одному критерию

Для определения общей функции полезности необходимо проверить условия независимости по полезности и независимости по предпочтению. Проверку первого условия можно совместить с предыдущим этапом построения однокритериальных функций полезности.

На рис. 8.3. приведена левая лотерея из рис. 8.2. Сначала лицу, принимающему решение, сообщается, что при нахождении эквивалента определенности он должен принять во внимание, что по остальным критериям имеются наилучшие значения (сверху справа на рис. 9.3.). Затем перед ЛПР ставится та же задача, но уже при предположении, что по прочим критериям имеются наихудшие значения (снизу справа на рис. 9.3.). Если эквивалент определенности в двух случаях одинаков, то делается вывод, что критерий не зависит по полезности от прочих критериев.

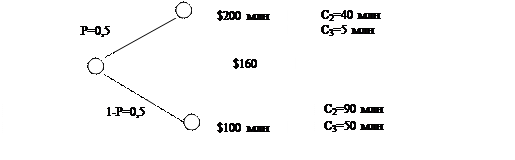Рис. 8.3. Проверка условий независимости по полезности

Отметим, что для полноты проверки условия независимости по полезности следует осуществлять эту проверку для всех лотерей (например, для лотереи 2 на рис. 8.2.). Однако часто довольствуются приближенной проверкой - только для первой из лотерей, используемых при построении однокритериальных функций полезности.

При проверке условия независимости по предпочтению рассматривают плоскости, где по осям отложены значения двух критериев. Пример такой плоскости для критериев C₁, C₂ приведен на рис. 8.4. Сначала предполагается, что по прочим критериям (в нашем случае — по критерию С₃) имеются наилучшие значения (С₃=5 тыс. человек).

Первоначально ЛПР должен определить свое предпочтение между альтернативами [(C₂)min; (C₁)max] и [(C₂)max; (C₁)min]. В нашем случае ЛПР сравнивает площадки для постройки аэропорта с оценками (40 мин., $200 млн) и (90 мин., $100 млн) -две крайние точки А и В на осях, при условии, что С₃=5 тыс. Предположим, что вариант А предпочтительнее. Это означает, что критерий «стоимости» более важен для ЛПР, чем критерий «расстояния».

Рис. 8.4. Проверка условия независимости по предпочтению

Далее определяется такая точка на шкале критерия С₁,что варианты А и К одинаково предпочтительны для ЛПР. Иначе говоря, ищется такая стоимость строительства С₁*, при которой одинаково предпочтительны варианты (90 мин., $100 млн) и (40 мин., С₁*). Затем точно такой же поиск точки безразличия осуществляется при С₃=50 тыс. Если результаты совпадают, то делается вывод, что пара С₁, С₂ не зависит по предпочтению от третьего критерия.

Для полной проверки условия независимости по предпочтениям следует рассмотреть все пары критериев. Однако при приближенной проверке выбираются один или два наиболее существенных критерия и прочие рассматриваются только в паре с ними.

При проверке и первого, и второго условий критерии, независимость от которых проверялась, имели крайние значения. Строго говоря, следовало бы рассмотреть и промежуточные значения, но обычно такая проверка считается достаточной. Что делать, если какие-то из условий независимости не выполняются? Теория не дает единственного ответа на этот вопрос. Предлагается определить группу независимых критериев, стоимость функции полезности для подгрупп зависимых и независимых критериев и общую функцию полезности «по частям» либо переформулировать задачу. Можно сказать, что нарушение условий независимости существенно усложняет задачу. Поэтому в дальнейшем обычно предполагается, что условия независимости выполняются.

Определение весовых коэффициентов

(коэффициентов важности) критериев

В MAUT используется понятие весов (коэффициентов важности) критериев. Считается, что ЛПР может найти коэффициенты - числа, которые определяют важность критериев. Отношения между весами критериев устанавливаются поиском точек безразличия на плоскостях двух критериев. В отличие от проверки условий независимости по предпочтению, по осям упорядочиваются значения критериев (от худших к лучшим).

На рис. 8.5. показана плоскость критериев С₁ и С₂. Альтернативы А и К находятся в отношении безразличия, которое определяется так же, как и при проверке условия независимости по предпочтению (см. рис. 8.4.).

$170 млн

Рис. 8.5. Определение отношения между весами критериев C₁ и С₂

В точке равновесия полезности альтернатив равны, что позволяет записать U($200 млн, 40 mhh.) = U($170 млн, 90 мин.).

Отсюда, используя полученные ранее однокритериальные функции полезности, находим W₂=0,4W_i. Аналогичным образом определяется соотношение между весами критериев С₁ и С₃.

Пусть w₃ = w₁ U($150 млн)=0,6 w₁, т.е. веса всех критериев выражены через вес наиболее важного из них, и критерии упорядочены по важности.

Для нахождения численного значения веса критерия С₁ (и, следовательно, всех критериев) ЛПР предлагается сравнить две стратегии, представленные на рис 8.6., и определить вероятность р, при которой обе стратегии равноценны.

Предположим, что такое р найдено. Тогда U(A)=U(B), или Wi =р. Пусть wi=0,55. Тогда w₂=0,22; w₃=0,33.

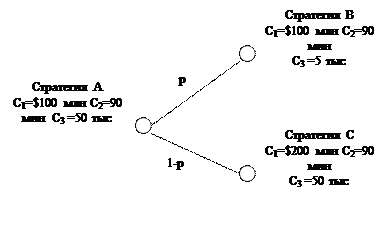
Рис. 8.6. Определение коэффициента w₁

После нахождения весов критериев и построения однокритериальных функций полезности задача считается решенной, т.е. общая функция полезности определена. В соответствии с теоретическими результатами остается установить ее вид. В нашем примере сумма коэффициентов важности критериев:

Sw_i =1,1

i=1

Считая полученное значение достаточно близким к единице, выбирается аддитивная форма представления функции полезности:

N

U(x) = SwiUi(x).

i=1

Зная оценки альтернатив (вариантов площадок), можем подставить их в эту формулу, определить полезность каждой альтернативы, сравнить полезности и выбрать альтернативу с наибольшей полезностью.

Дата добавления: 2014-01-07