Лекция 6. Метод конформных отображений

Электродные системы со сложными двумерными электростатическими полями могут быть рассчитаны методом конформных отображений. Основная идея этого метода состоит в замене сложных полей – простыми полями, для которых решения известны. К таким простым полям относятся поля плоского или цилиндрического конденсатора вдали от их краев. Метод конформных отображений является практическим применением теории функции комплексного переменного. Конформное отображение – это непрерывное отображение, сохраняющее форму бесконечно малых (б.м.) фигур. Для конформного отображения выполняется свойство постоянство углов и постоянство растяжений. Название происходит от позднелатинского – conformis – подобный, непрерывное отображение, сохраняющее форму бесконечно малых фигур: например, б.м. круг остается б.м. кругом; углы между линиями в точке их пересечения друг с другом не изменяются. Область применения метода конформных отображений для расчета электрических полей – двумерные электростатические поля.

Конформное преобразование отображает каждую точку z = x + j×y реального расчетного поля, описывающегося комплексной плоскостью, в точку w = u + j×v другой комплексной плоскости, с более простой конфигурацией поля. Основная сложность метода – нахождение вида функции для данной реальной электродной системы. На практике, при попытках найти функцию конформного отображения, используют либо специальные каталоги конформных отображений [11,12], либо ищут ее посредством последовательных проб.

Предположим, что мы знаем вид некоторого преобразования z = f(w) или обратного преобразования w = f(z), которое устанавливает взаимно однозначное соответствие между двумя комплексными плоскостями со сложной (z) и простой (w) конфигурацией поля. Коэффициентом преобразования называется отношение dw/dz.

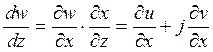, (2.93)

здесь использованы соотношения:

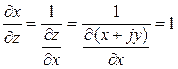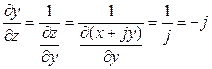, . (2.94)

Аналогично можно записать:

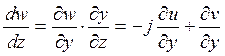. (2.95)

Два комплексных числа равны, если у них равны порознь действительные и мнимые части. Сравнивая значения коэффициента преобразования, приведенные в выражениях (2.93) и (2.95) можно записать:

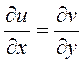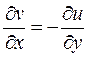; (2.96)

Выражения (2.96) известны под названием условий Коши-Римана. Используя различные формы представления комплексных чисел, коэффициент преобразования можно записать в виде:

,

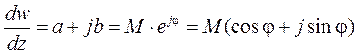где 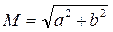- коэффициент изменения длины отрезков при преобразовании, а tg(j) = b/a (j - угол поворота отрезков при преобразовании). Из соотношений Коши-Римана, получим:

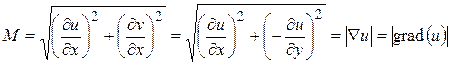(2.97)

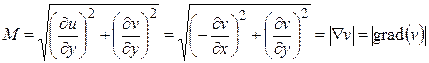(2.98)

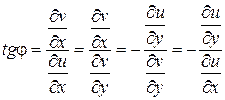(2.99)

Из соотношений (2.97) – (2.98) следует, что коэффициент конформного преобразования М является относительной напряженностью электрического поля, а каждая из функций u и v может быть выбрана в качестве потенциала на новой комплексной плоскости w = f(u,v). Этот вывод может быть проверен другим способом. Если функции u и v могут быть выбраны в качестве потенциала, то каждая из них должна удовлетворять уравнению Лапласа: D u =0 и D v =0. Это можно проверить непосредственным повторным дифференцированием условий Коши-Римана. Продифференцируем первое условие по х, а второе по у; сложим результат; перенесем в левую часть записи все значащие производные и оставим справа нуль:

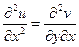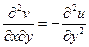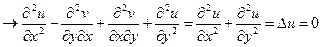; ; . (2.100)

Из полученного выражения следует, что функция u удовлетворяет уравнению Лапласа (1.25), (1.30) и может быть принята за потенциал. Продифференцируем 1-е условие по у, а 2-е - по х:

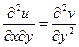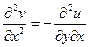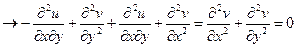; ; , (2.101)

т.е. и функция v также удовлетворяет уравнению Лапласа и также может быть принята за потенциал. Поскольку силовые и эквипотенциальные линии на плоскости z = f(x,y) взаимно перпендикулярны, а конформное преобразование оставляет неизменными углы между линиями в точке их пересечения, то из (2.97) ¸ (2.101) следует, что если функция u принята, например, за потенциал, то тогда линия с v =const – является силовой линией. Если же v – потенциал, то u =const – силовая линия. Какая из функций u или v является потенциалом, а какая силовой линией, следует определять из анализа конформного преобразования поля на исходной плоскости z = f(x,y) в поле на плоскости w = f(u,v). Любая функция z=f(w) (или w=f(z)) дает нам решение какой-либо задачи электростатики. Можно придумать произвольную функцию, найти для неё решения, а затем к найденным решениям подобрать соответствующую электродную систему. Таким методом (задом наперед) было найдено множество решений электростатических задач.

При нахождении напряженности электрического поля методом конформных отображений следует учитывать следующее важное обстоятельство. Картина электрического поля полностью определяется геометрическими параметрами электродной системы независимо от пространственного масштаба и приложенного напряжения. Поэтому поле может быть описано напряженностью, отнесенной к единице напряжения или длины. Выражения (2.97)-(2.98) представляют собой именно такую относительную напряженность. Для получения реальной напряженности необходимо учесть действительно приложенное напряжение и фактическое расстояние между электродами. Это делается умножением выражений (2.97)-(2.98) на коэффициент масштаба К_м. Пусть расстояние между электродами в плоскости w равно u ₂- u ₁ (v ₂- v ₁), если за эквипотенциальные линии приняты функции u или v, соответственно. Тогда коэффициент масштаба принимает вид:

К_м = U /(u ₂- u ₁) или К_м = U /(v ₂- v ₁). (2.102)

Цилиндрический конденсатор. Хотя расчет электростатического поля цилиндрического конденсатора приведен в §2.5, рассмотрим его в качестве примера применения метода конформных отображений. Поле цилиндрического конденсатора (поле двух концентрических окружностей) на плоскости ху может быть отображено в однородное поле (поле плоского конденсатора) следующим преобразованием:

z = e^w; x + j×y = e^u+jv = e^u (Cos v + j ×Sin v).

Произведем разделение действительных и мнимых частей:

Прямая линия на реальной плоскости z, проходящая через начало координат с углом наклона к оси х равным v =const переходит в прямую линию на плоскости w, параллельную оси абсцисс.

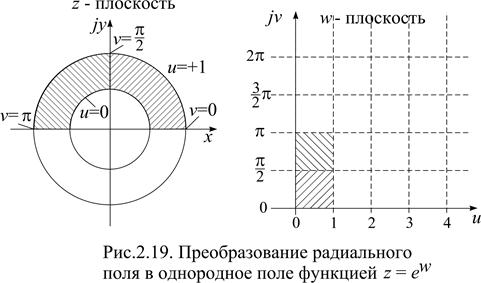
При u = const на плоскости w получается система прямых линий, параллельных оси ординат. На плоскости z они соответствуют системе концентрических окружностей. Очевидно, что линии с u = const следует принять за потенциальные линии, а v – за силовые линии поля. Расчет напряженности будем проводить по формуле (2.97):

; .

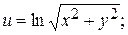
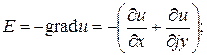
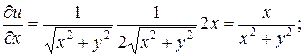
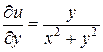
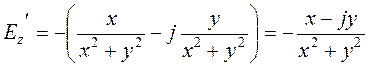
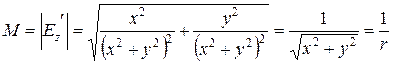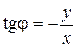Длина преобразуемого малого отрезка при переносе с плоскости z на плоскость w изменяется в 1/ r раз, где r – расстояние до центра окружностей. Чем дальше от центра, тем меньше коэффициент изменения длин отрезков. Переносимый отрезок поворачивается на угол j = arctg(- y/x). Угол между лучом, идущим из начала координат в середину преобразуемого отрезка, и осью х становится равным нулю. Все радиусы на z - плоскости превращаются на w - плоскости в линии параллельные оси u. Масштабный коэффициент

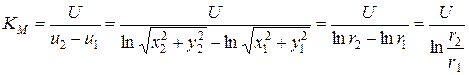
Напряженность

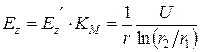(2.103)

Полученная формула (2.103) совпадает, как и следовало ожидать в силу теоремы о единственности, с выражением (2.18), полученным с помощью теоремы Остроградского-Гаусса.

Поле внутри прямого угла, образованного двумя плоскостями

В качестве другого примера применения метода конформных отображений рассмотрим поле, образованное двумя бесконечными проводящими взаимно перпендикулярными плоскостями. Очевидно, что такая электродная система имеет трансляционную симметрию с бесконечно малым шагом трансляции вдоль плоскостей и плоскость симметрии, проходящую под углом 45° к каждой из плоскостей. Такое поле сводится к двумерному полю, а для определения его параметров достаточно рассчитать характеристики поля между одной из плоскостей и плоскостью симметрии. Для двумерных полей может быть применен метод конформного отображения. Поле в z – плоскости, перпендикулярной линии пересечения заряженных плоскостей, показано на рис.2.20а. За оси х и у приняты линии пересечения заряженных плоскостей с z – плоскостью. Поле внутри прямого угла, образованного двумя плоскостями, преобразуется в однородное поле преобразованием w = z ². Покажем это:

w = u + jv = z ² = (x + jy)² = x ² + j 2 xy – y ²; u = x ²– y ²; v = + j 2 xy.

При u = const линии, параллельные оси v на плоскости w, преобразуются в семейство равнобочных гипербол x ²– y ² = а ² на плоскости z. Ось 0 х является действительной (фокальной) осью гипербол, а ось у её мнимой осью. Прямая линия, проходящая через начало координат под углом 45° к оси х (u = 0; y = x), представляет собой линию пересечения z – плоскости с плоскостью симметрии и является асимптотой гипербол. Угол пересечения гипербол с осью х равен 90°, т.е. линии функции u = х ²- у ² перпендикулярны эквипотенциальной линии х (поверхности заряженной плоскости х).

Функции v = 2 xy при различных значениях v описывают другое семейство равнобочных гипербол, у которых оси х и у являются асимптотами, а линия у = х является фокальной осью. На рис.2.20а представлены гиперболы с v = 4, 16, 36. При v = 0 гипербола вырождается в оси координат х и у, которые совпадают с заряженными плоскостями. Поскольку поверхность заряженных плоскостей является поверхностью одинакового потенциала, очевидно, что именно функция v должна быть принята за потенциальную функцию на плоскости w. В этом случае функция u представляет собой силовую функцию. Поле двух бесконечных взаимно перпендикулярных плоскостей (оси х и у на z – плоскости) превращается в однородное поле бесконечной заряженной плоскости (ось v на w – плоскости).

Конформное преобразование, сохраняя форму бесконечно малых фигур, может существенно изменить форму конечных фигур. В качестве примера такого изменения приведено преобразование квадрата abcd c координатами а (0,8;0,8), b (0,8;4), c (4;4), d (4;0,8) на z - плоскости в криволинейный четырехугольник a¢b¢c¢d¢ с координатами а¢ (0;1,28), b¢ (-15,36;6,4), c¢ (0;32), d¢ (15,36;6,4) на w - плоскости.

Определим относительную напряженность электростатического поля заряженных плоскостей рис.2.20а. Из двух формул (2.97) и (2.98) для определения напряженности будем использовать (2.98), поскольку именно функция v = 2 xy описывает систему эквипотенциальных поверхностей (линий). Линейный коэффициент преобразования:

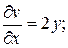
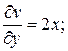
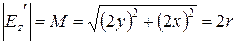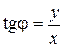, (2.104)

Длина преобразуемого малого отрезка при переносе с z - плоскости на w - плоскость увеличивается в 2 r раз, где r = х ²+ у ² – расстояние на z - плоскости от начала координат до центра отрезка. Переносимый отрезок поворачивается на угол j = arctg(y/x). Происходит удвоение угла между лучом, идущим из начала координат в середину отрезка, и осью х. Масштабный коэффициент К_м = U /(v ₂- v ₁) = U /(2 x ₂ y ₂-2 x ₁ y ₁). Напряженность поля определится умножением относительной напряженности на масштабный коэффициент: Е = E¢×K_м. Пусть масштабный коэффициент равен К_м =100 в/м. Определим напряженность поля в двух точках на заряженной плоскости: более близкой к углу пересечения плоскостей n 1(1;0) и отдаленной от него n 2 (5;0).

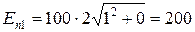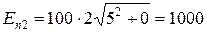в/м, ×в/м.

Чем ближе к углу, тем меньше напряженность поля. Это результат можно было ожидать из картины поля рис.2.20: расстояние между эквипотенциальными линиями уменьшается при удалении от угла. Любое углубление (вмятина, впадина, каверна, трещина и т.п.) на поверхности электрода может быть приблизительно описано рассмотренной задачей. Тогда, учитывая результаты предыдущего параграфа, можно заключить: вблизи острия или выступа напряженность электрического поля повышается, а вблизи впадины или отверстия она слабеет. Аналогичная рис.2.20а картина поведения силовых и эквипотенциальных линий наблюдается вблизи точки ветвления поля от двух одноименных зарядов (§2.11).

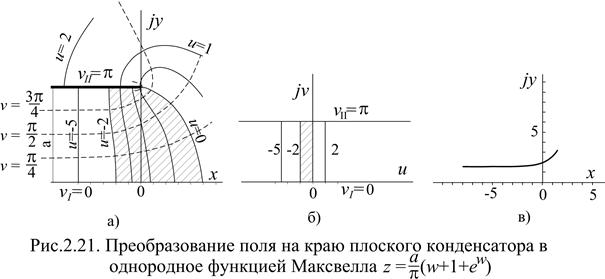
Поле на краю плоского конденсатора (профиль Роговского)

Поместим начало координат на z - плоскости так, чтобы ось х была параллельна плоскостям обкладок конденсатора и находилась от них на одинаковом расстоянии a. Ось у перпендикулярна обкладкам и проходит через их края. Функцию отображения поля на краю плоского конденсатора в однородное поле получил Ю. К. Максвелл в 1881 г. в виде:

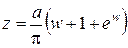. (2.105)

После разделения переменных получаем:

,

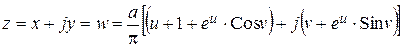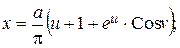
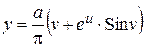
При v_I = 0, y = 0, 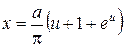. При v_II = p, y = a, .

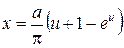Очевидно, что за потенциальную функцию следует выбрать функцию v.

,

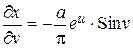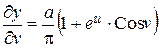
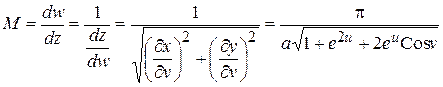
Учитывая, что К_м = U/(v_II-v_I) = U /p

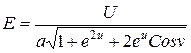(2.106)

При u < -5 в области от v_I =0 до v_II =p получается практически однородное поле с напряженностью U/a. При u ®0 напряженность на электроде (v = v_II= p)сильно возрастает и стремиться к бесконечности при u =0. Наибольшая напряженность в реальных системах не обращается в нуль:

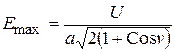. (2.107)

При конечной толщине обкладки конденсатора v ¹p и напряженность остается конечной. Величину v следует подбирать так, чтобы эквипотенциальная поверхность совпала с реальной поверхностью обкладки конденсатора. Пусть v = 174° = 29p/30, тогда отношение напряженности у края электрода к средней напряженности:

.

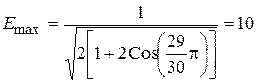Видно, что у даже довольно тупого края напряженность резко возрастает. Это отношение можно сделать близким к единице, если поверхность электрода выполнить в виде эквипотенциальной поверхности с v £ p/2. Такой профиль электрода называется профилем Роговского (рис.2.21в). При расстоянии а = p (между обкладками расстояние 2p) он имеет координату v = p/2 и для него x = u +1; y = p/2+ e^u, т.е. у = p/2+ e ^{(х -1)} (2.108)

Профиль Роговского имеет большое практическое значение в экспериментах по пробою в поле, близком к однородному для устранения краевого эффекта [3]. В центре устройства с электродами Роговского имеет место однородное поле.

Поле расщепленных проводов.

В линиях электропередачи высокого напряжения фазовый провод расщепляют на несколько проводников в целях уменьшения потерь передаваемой мощности из-за коронного разряда. Для описания поля расщепленного

провода можно пользоваться функцией отображения 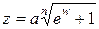, где n –

число отдельных проводников, на которые расщепляется фазовый провод. В качестве иллюстрации метода конформных отображений рассмотрим расщепление на два провода (n =2). (Заметим, что этот случай достаточно просто может быть решен методом изображений [1])

Пусть плоскость z перпендикулярна расщепленным проводам. Выберем ось х на z плоскости таким образом, чтобы она проходила через оси проводов. Пусть ось y проходит через середину отрезка между проводами. Решение существенно упрощается, если находить не функции x,y = f(u,v), а функции u,v = f(x,y). Разделяя действительную и мнимую части, получим:

,

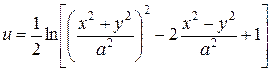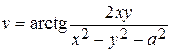
Эквипотенциальным линиям соответствует функция u. Чтобы функция u равнялась нулю, логарифм должен быть равен нулю, а выражение в квадратных скобках должно быть равно 1. Тогда выполняется соотношение:

(х ²+ у ²)² = 2 а ²(х ²- у ²)

Эта функция проходит через начало координат z - плоскости. При u в диапазоне -1,28 < u < 0 на z - плоскости наблюдаются круговые области справа и слева от оси у. При u £ -1.28 это практически точки с координатами х = - а и х = а. При u > 0 решениями являются замкнутые кривые, которые при возрастании u приближаются по форме к окружностям. Эти кривые представляют собой потенциальные линии поля двух цилиндров с зарядами одного знака, т.е. поля двух проводов с одним потенциалом. Наибольший интерес представляют точки на поверхности проводов р ₂ и р ₁, в которых, соответственно, наблюдается наибольшая и наименьшая напряженность поля. Точка р ₂ находится на поверхности провода в наиболее удаленной от другого провода точке и имеет координаты:

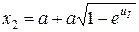, у = 0.

Точка р ₁ находится на поверхности провода в наиболее близкой к другому проводу точке и имеет координаты:

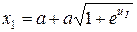, у = 0.

Значение u_I соответствует эквипотенциальной поверхности совпадающей с поверхностью провода. Относительная напряженность в произвольной точке определится выражением (2.97):

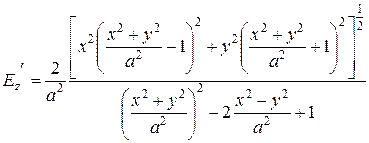. При у = 0 .

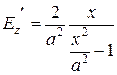Для точек р ₁ (р ₂): ;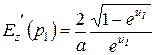

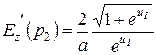
Введем следующие характеристики расщепления:

а) r – радиус провода; б) s – расстояние между проводами одной фазы;

в) b = s/r – отношение расстояния между проводами к их радиусу;

г) p = (a+r)/ r – отношение расстояния от начала координат до точки с максимальной напряженностью к радиусу провода.

,

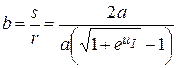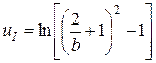
С учетом масштабного коэффициента для точки р₂ получаем:

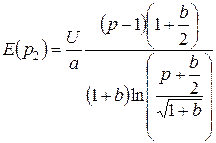. (2.109)

При s®0 электродная система превращается в систему двух коаксиальных цилиндров (b =0, s =0) (см.(2.18)):

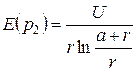
Обычно для линии электропередачи p ³ 200.

Дата добавления: 2014-01-07