Лекция 7. Метод эквивалентных зарядов

Основы метода

Метод эквивалентных зарядов позволяет рассчитывать поле наложением нескольких единичных полей. Суть метода состоит в замене сложной электродной системы на более простую совокупность дискретных зарядов, для которой можно рассчитать характеристики электрического поля в любой требуемой области пространства. По условиям задачи известными являются геометрические размеры электродов и их потенциалы. Расчеты по методу эквивалентных зарядов проводятся в несколько этапов.

1. Задание координат дискретных пробных зарядов. Сложная электродная система заменяется набором дискретных пробных зарядов, таких как точечные заряды, линейные или кольцевые заряды. Координаты размещения зарядов задаются из соображений симметрии задачи и являются известными, в то время, как сами величины зарядов на первом этапе не известны. Координаты дискретных зарядов должны выбираться в такой области поля, в которой расчеты характеристик производиться не будут. Например, внутри или на поверхности электродов.

2. Задание координат реперных точек. Задаются координаты реперных (контурных, контрольных) точек, в которых известны величины потенциалов. Эти точки выбираются, как правило, на поверхности электродов. Количество контрольных точек должно совпадать с числом задаваемых пробных зарядов.

3. Определение потенциальных коэффициентов. Определяются расстояния от каждого дискретного заряда до каждой контрольной точки. Находится величина потенциального коэффициента для каждой пары: заряд – контрольная точка. Поскольку заряды выбираются дискретными, то для них известны формулы определения величины потенциала, создаваемого зарядом в любой точке пространства, если известно расстояние до требуемой точки. Например, определим величину частичного потенциала, создаваемого в 7-ой контрольной точке 5-ым пробным точечным зарядом с величиной q ₅. Назовем эту величину частичным потенциалом, создаваемым в точке 7 зарядом 5, и обозначим её символом j₇₅. По формуле для потенциала, создаваемого точечным зарядом j₇₅ = q ₅/(4pe₀e× r ₇₅)= p ₇₅× q ₅, где r ₇₅- расстояние между реперной точкой 7 и пробным зарядом 5, а p ₇₅- соответствующий потенциальный коэффициент. Обозначим координаты пробных зарядов как (x_m,y_m,z_m), а реперных точек (a_n,b_n,c_n). Тогда

,

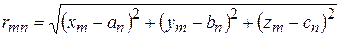а потенциальные коэффициенты вычисляются по формуле p_mn =1/(4pe₀e× r_mn) и представляют собой определённые числа, поскольку координаты всех точек известны из этапов расчета 1 и 2. Частичный потенциал j _mn = p_mn × q_n.

4. Определение величины пробных зарядов. В соответствии с принципом суперпозиции величина потенциала в реперной точке складывается из суммы частичных потенциалов, создаваемых в этой точке всеми пробными зарядами:

p ₁₁× q ₁+ p ₁₂× q ₂+ p ₁₃× q ₃+ ××+ p _{1 n} × q ₁ = U ₁.

p ₂₁× q ₁+ p ₂₂× q ₂+ p ₂₃× q ₃+ ××+ p _{2 n} × q ₂ = U ₂.

p ₃₁× q ₁+ p ₃₂× q ₂+ p ₃₃× q ₃+ ××+ p _{3 n} × q ₃ = U ₃. (3.20)

× × × × × × × × × × × × × × × × × × × ×

p_{n 1}× q ₁+ p_{n 2}× q ₂+ p_{n 3}× q ₃+ ××+ p_nn × q_n = U_n

Получается система n - линейных уравнений с n -неизвестными зарядами q_n. Потенциальные коэффициенты p_mn были численно определены на предыдущем этапе расчета, а потенциалы U_n известны по условию выбора реперных точек. Система линейных уравнений (3.20) решается на ЭВМ стандартными методами, например, методом Гаусса. В результате решения величины пробных зарядов становятся известными.

5. Определение потенциалов в требуемой области поля. Для определения характеристик поля в интересующей области следует задать координаты точек, в которых будут рассчитываться потенциалы. Потенциал в выбранной точке в соответствии с принципом суперпозиции будет равен сумме частичных потенциалов, создаваемых в этой точке всеми пробными зарядами. Величина и положение (координаты) пробных зарядов были определены на предыдущих этапах расчета.

6. Определение напряженности поля. Для расчета напряженности поля (E =-gradj) нужно знать потенциалы в двух соседних (в идеале бесконечно близких) точках поля j₁ и j₂ с координатами (x ₁, y ₁, z ₁) и (x ₂, y ₂, z ₂), которые выбираются и рассчитываются на шаге 5. Для повышения точности расчетов точки поля должны выбираться как можно ближе друг к другу. Тогда проекции вектора напряженности на оси x, y, z будут, соответственно, равны:

E_x =-(j₂-j₁)/(x ₂- x ₁), E_y =-(j₂-j₁)/(y ₂- y ₁), E_z =-(j₂-j₁)/(z ₂- z ₁).

Величина вектора напряженности определяется как: ,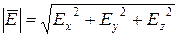

а направляющие косинусы вектора напряженности по осям x, y, z равны:

.

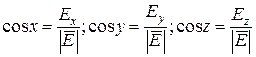Поле двух заряженных проводящих шаров

Одним из устройств измерения разрядного напряжения воздушных промежутков является шаровой разрядник. Два заряженных металлических шара приближаются друг к другу до тех пор, пока между ними не произойдет разряд. Разрядное расстояние S между шарами шарового разрядника (наименьшее расстояние между точками поверхностей шаров, точки А ₇ и А ₈ рис.3.6 обычно выбирается в диапазоне 0,05¸0,5 D, где D – диаметр шара. Пусть имеется два проводящих шара 1 и 2, заряженных до потенциала U ₁ и U ₂. Требуется определить напряженность поля в промежутке между шарами. Для расчета характеристик поля уединенного проводящего шара в силу сферической симметрии задачи мы помещали весь заряд шара в его центр и сводили задачу к расчету поля точечного заряда. В случае двух близко расположенных шаров, произвести подобную замену нельзя, т.к. распределение зарядов по поверхности шаров перестает быть равномерным. Решение задачи двух шаров методом отражений приведено в §2.17. Решим эту же задачу методом эквивалентных зарядов. Задача двух шаров (см. рис.3.6) имеет осевую симметрию, с осью С _¥, проходящей через центры шаров. В силу симметрии расчет поля в пространстве сводится к расчету поля в плоскости, содержащей ось симметрии, например, в плоскости рис.3.6. За ось Х выберем ось симметрии С _¥, а за ось Y – перпендикуляр к оси симметрии. Выберем начало декартовой системы координат в середине между шарами. Задача симметрична относительно оси Х и Y. Для получения численной картины поля достаточно определить характеристики поля в одном из квадрантов. Объемный заряд в расчетах учитываться не будет. Наибольший интерес представляют данные вблизи оси Х.

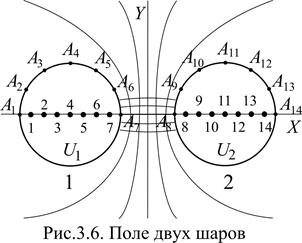1 этап. Выберем места расположения пробных зарядов внутри шаров c равными между собой расстояниями и расстоянием от поверхности до крайних точек как показано на рис.3.6. Координата Y каждой точки равна 0 (y _m =0), а координата Х определяется следующим способом:

для точек 1-7 х_m = - S /2- D + m×D /8,

для точек 8-14 х_m = x_{m -7}+ S + D

2 этап. Реперные точки выберем на поверхности шаров таким образом, чтобы длина дуги между ближайшей парой точек была постоянной. Центральный угол в данном случае меняется на p/6 от p до 0 и равен j _{А 1}=p, j _{А 2}=5p/6, j _{А 3}=2p/3, j _{А 4}=p/2, j _{А 5}=p/3, j _{А 6}=p/6, j _{А 7}=0. Координаты х точек А ₁ – А ₇ равны: х_n = Cos[p(7- n)/6]× D /2-(S+D)/2. Координаты у точек А ₁ – А₇ равны y_n = Sin[p(7- n)/6]× D /2/

Для точек 8-14 выполняются следующие соотношения х_n = х_{n -7}+ S + D; y_n = y_{n -7}.

3 этап. Координаты всех точек заданы, и можно приступать к расчету потенциальных коэффициентов по формуле

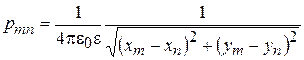
Далее выполняются этапы 4, 5 и 6.

Дискретные эквивалентные заряды

Для воспроизведения поля, создаваемого расположенными на поверхности электродов зарядами, в методе эквивалентных зарядов используется три типа дискретных зарядов: точечные, линейные и кольцевые заряды. Плотность заряда в случае линейных и кольцевых зарядов предполагается постоянной для одного дискретного заряда. Выбор того или иного вида дискретного эквивалентного заряда определяется формой и симметрией расположения электродов. Так для параллельных цилиндрических электродов используются линейные заряды. Для электродов в форме оболочек более подходящими являются кольцевые заряды. Для сферических электродов можно использовать как точечные, так и кольцевые заряды.

Потенциал в произвольной точке поля М(x,r), создаваемый дискретным зарядом при использовании обозначений рис.3.7 имеет вид:

точечный заряд

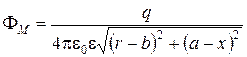(3.21)

линейный заряд

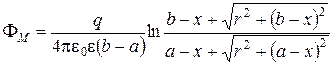(3.22)

кольцевой заряд

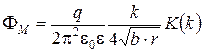, (3.23)

где , .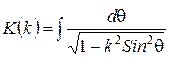

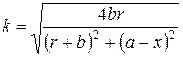Расчеты потенциальных коэффициентов 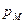для линейных и кольцевых зарядов проводятся непосредственно по формулам 3.21 и 3.22 с учетом того, что потенциал 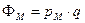. Для расчета соответствующего коэффициента для каждой пары эквивалентный кольцевой заряд – реперная точка необходимо сначала вычислить величину коэффициента k в 3.24, который примет некоторое определенное число. Затем вычисляется функция K(k). Вычисление этой функции не представляет сложности, поскольку на любом из языков программирования высокого уровня имеются подпрограммы вычисления определенных интегралов различными методами. Окончательно потенциальный коэффициент 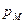рассчитывается по 3.23.

Расположение эквивалентных зарядов на плоскости позволяет рассчитывать поля при плоских тонких формах электродов, например, промежуточные прокладки вводов или фигурных изоляторов элегазовых устройств. Такое расположение эквивалентных зарядов в значительной степени соответствует реальным физическим поверхностным зарядам. При этом как потенциальные, так и силовые характеристики поля физически правильно воспроизводятся и могут быть рассчитаны в любой точке.

Реальные электродные системы, как правило, имеют сложные геометрические формы или граничные поверхности, которые описываются полиномами высоких степеней. С целью упрощения расчетов целесообразно ограничиваться линейным приближением при описании координат поверхности электродов и плоскостей зарядов. Если электродная система имеет цилиндрическую симметрию (С_¥), то поверхностную плотность реальных зарядов (s) можно свести к эквивалентным кольцевым зарядам, у которых изменяются значения заряда и диаметра. Используя обозначения рис.3-7в, можно сказать, что радиус кольцевого заряда b = f(x) и его линейная плотность t= f(x) = q(x) /(2p b (x)).

При расчетах поля в слоистых диэлектриках с различными значениями диэлектрической проницаемости слоев граница раздела влияет на электростатическое поле таким же образом, как и поверхностный заряд. Этот поверхностный заряд, как и заряд на металлических электродах, можно заменить эквивалентным зарядом, помещенным внутри диэлектрика. Поверхностный заряд на границе раздела может быть заменён точечными или линейными эквивалентными зарядами, помещёнными внутри обеих сред, причем для поля в одной среде учитывается заряд, помещенный в другую среду, и наоборот.

Дата добавления: 2014-01-07