Агрегатные индексы. Методика их построения

Понятие об индексах, их классификация. Индексная символика

Тема 1.6 Индексы

"Индекс" в переводе с латинского - указатель или показатель. В статистике индексом называют показатель относительного изменения данного уровня исследуемого явления по сравнению с другим его уровнем, принятым за базу сравнения. В качестве такой базы может быть использован или уровень за какой-либо прошлый период времени (динамический индекс), или уровень того же явления по другой территории (территориальный индекс). Индексы являются незаменимым инструментом исследования в тех случаях, когда необходимо сравнить во времени или пространстве две совокупности, элементы которых непосредственно суммировать нельзя.

Индексы могут выступать, как показатели динамики и выполнения плана.

Индексы вычисляемые для пространственного сравнения называются территориальными.

Различают индексы физического объема (объемные) и качественные (индексы качественных показателей). С точки зрения охвата элементов совокупности различают индивидуальные (однотоварные), общие (сводные), групповые (субиндексы) (ПРИЛОЖЕНИЕ 4).

Индивидуальные индексы дают сравнительную характеристику отдельных элементов той или иной совокупности, который получается путем сравнения двух абсолютных величин, характеризующих уровень изучаемого явления для двух разных периодов.

Величина, которая стоит в числителе индексного отношения характеризует уровень отчетного периода, а величина, с которой сравнивают, т.е. стоящая в знаменателе, характеризует уровень базисного или планового периода.

Индекс может быть выражен в виде процента или коэффициента. Общие индексы характеризуют изменение совокупности в целом. Групповые индексы или субиндексы охватывают какую-то часть элементов совокупности.

В зависимости от методики расчета различают индексы агрегатные и индексы средние от индивидуальных.

Агрегатные – это основная форма общего экономического индекса.

Средние от индивидуальных – это производная форма, которая получается путем преобразования агрегатного индекса.

В статистике используется следующая система условных показателей:

z – себестоимость единицы продукции (качественный показатель);

p – цена единицы продукции (качественный показатель);

t – Трудоемкость единицы продукции (качественный показатель);

w(1/t) – производительность труда (качественный показатель);

Т – общее время, затраченное на выпуск продукции (объемный показатель);

Иногда Т – это среднесписочная численность работников.

q – объем произведенной или реализованной продукции (объемный показатель);

В международной статистике индивидуальные и общие индексы принято обозначать символами i и I соответственно.

Помимо этого используются определенные символы для обозначения индексных показателей.

Показатели, относящиеся к отчетному периоду обозначаются подстрочной цифрой "1".

Показатели, относящиеся к базисному периоду обозначатся подстрочной цифрой "0". Показатели, относящиеся к плановому периоду обозначаются подстрочной буквой "пл". Например: i = р₁ / р₀ - индивидуальный индекс цен.

Для того, чтобы рассчитать общий индекс, надо прежде всего преодолеть несуммарность отдельных элементов изучаемого явления. Это достигается путем введения в индекс какого-то дополнительного и неизменного показателя, экономически тесно связанного с индексным показателем, такой показатель называют показателем соизмерения или весом индекса. При индексировании цен в качестве веса вводится объем реализованной или произведенной продукции.

Индекс, в числителе и знаменателе которого стоит сумма произведений индексируемой величины на вес называется агрегатным индексом или индексом в агрегатной форме. Причем: индексируемый показатель нужно брать на разных уровнях, а именно:

в числителе - на уровне отчетного;

в знаменателе - на уровне базисного;

а вес на одном уровне - либо отчетном, либо базисном.

Например: агрегатный индекс физического объема имеет вид:

.

Построение индексов качественных показателей будем рассматривать на примере агрегатного индекса цен.

В индексе в числителе стоит количество произведенной продукции в отчетном периоде по ценам этого же периода, а в знаменателе этого индекса объем произведенной продукции отчетного периода, но по ценам базисного периода (это величина условная), индекс называется индексом цен Пааше:

.

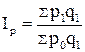Разница между числителем и знаменателем в агрегатном индексе цен покажет прирост объема произведенной продукции за счет фактора изменения цен в текущем периоде по сравнению с базисным.

Построение индексов объемных показателей рассмотрим на примере построения индекса объема произведенной или реализованной продукции:

.

Для того, чтобы нейтрализовать влияние изменения цен на объем произведенной продукции мы должны зафиксировать цены на уровне базисного периода. Тогда с помощью индекса мы сможем подсчитать экономический эффект от изменения производства или реализации продукции.

Общее правило построения агрегатных индексов: для построения индексов качественных показателей веса нужно фиксировать на уровне отчетного периода, количественных показателей - на уровне периода базисного.

ПРИМЕР: Себестоимость и объем продукции завода характеризуются следующими данными:

Изделие	Себестоимость единицы продукции, тыс. руб.	Выработано продукции, тыс.шт.
ххх1 (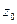)	ххх2 (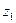)	ххх1 ()	ххх2 ()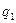
СП-2
МК-1

Определить общие индексы:

1) затрат на продукцию;

2) себестоимости продукции;

3) физического объема продукции.

Сделать выводы.

Решение:

По данным таблицы рассчитаем:

1) а) Общий индекс затрат на производство (по обоим видам продукции) (I_zq):

Для удобства построения индексов в теории статистики разработана символика, т.е. каждая анализируемая величина имеет свое обозначение. Так, количество единиц конкретного вида произведенной продукции обозначается q, себестоимость единицы изделия - z.

Тогда

или 97,1%, т.е. общие затраты на производство продукции снизились на 2,9%.

б) общий индекс себестоимости продукции:

Так, агрегатный индекс себестоимости (Iz) определяется по формуле:

,

где z₀, z₁ - себестоимость каждого вида продукции (товара) соответственно в базисном (ххх1) и отчетном (ххх2) годах (индексируемый показатель);

q₁ - объем каждого вида продукции (товара) в отчетном периоде:

или 80,0%, т.е. себестоимость продукции в среднем по двум видам продукции снизилась на 20% в отчетном периоде (ххх2 году) по сравнению с базисным (ххх1 годом).

в) общий индекс физического объема продукции (I_q):

или 121,4%, т.е. объем выпускаемой продукции в натуральном выражении в среднем вырос на 21,4%.

2) Определим абсолютное изменение суммы затрат на производство в ххх2 году по сравнению с ххх1 годом:

∆zq = ∑z₁q₁- ∑z₀q₀=3400-3500=-100(млн.руб.),

в том числе за счет:

а) изменения уровней себестоимости: ∆zq(z) = ∑z₁q₁-∑z₀q₁=3400-4250= - 850(млн.руб.)

б) изменения физического объема продукции (товаров):

∆zq(q) = ∑ z₀q₁ - ∑ z₀q₀ =4250-3500=+ 750 (млн.руб.).

При этом должно соблюдаться следующее равенство:

∆zq = ∆zq(z) +∆zq(q)=(-850)+(+750)= -100 (млн.руб.)

3) Между исчисленными индексами существует взаимосвязь. Произведение агрегатного индекса себестоимости на агрегатный индекс физического объема равно агрегатному индексу затрат на производство продукции:

Iz×Iq = Izq=0,8×1,214= 0,971 или 97,1%.

Вывод: как показывают произведенные расчеты, общие затраты на производство продукции снизились на 2,9% или 100 млн. рублей. Причем снижение себестоимости продукции в среднем по двум видам продукции на 20% обеспечило экономию затрат на 850 млн.рублей. В то же время прирост объема выпускаемой продукции в среднем на 21,4% повлек за собой перерасход затрат на производство продукции в размере 750 млн.рублей.

Дата добавления: 2014-01-07