Выборочное наблюдение

Контрольные задания

Имеются следующие данные по группе из 20 студентов заочного отделения (таблица 2):

Таблица 2. Варианты выполнения контрольного задания

№ п/п	Вариант
Рост, см	Вес, кг	Доход, у.е./мес.	IQ (тест Айзенка)	Тет-радь, листов	Воз-раст, лет	Соот-ношение «рост/вес»	Стаж работы, мес.	Кол-во друзей, чел.	Время решения контрольной, час.
							3,533			8,5
							2,623			6,2
							2,875			6,8
							3,375			12,0
							3,000			7,5
							2,828			10,0
							3,255			7,2
							2,726			4,2
							2,429			3,5
							2,361			9,5
							2,342			7,8
							2,672			8,0
							2,356			6,0
							2,559			4,8
							2,173			8,6
							2,095			10,0
							2,342			4,5
							2,011			12,5
							2,691			10,5
							2,021			6,5

Построить интервальный ряд распределения признака и его график, рассчитать среднее значение признака и изучить его вариацию.

Выборочное наблюдение – способ не сплошного наблюдения, при котором обсуждается не вся совокупность, а лишь часть её, отобранная по определённым правилам выборки и обеспечивающая получение данных, характеризующих всю совокупность.

Таблица №11 “Выборочное наблюдение”

	генеральная совокупность	выборка
средняя величина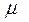
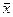
относительная величина	π	P
дисперсия		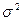S^2
коэффициент корреляции		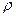R
	N	K(n)

Ошибки выборочного наблюдения называются ошибками репрезентативности. Размер ошибки выборки и методы её определения зависят от вида и схемы отбора.

Таблица №12: “Ошибки выборочного наблюдения”

способы отбора	ошибки	для многозначного признака	для альтернативного признака
повторный отбор	средняя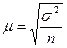
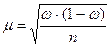
предельная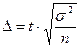
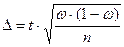
бесповторный отбор	средняя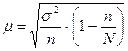
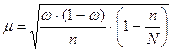
предельная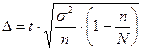

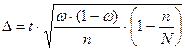
Различают четыре вида отбора совокупности единиц наблюдения:

1. Случайный – жеребьёвки (тиражи выигрышей).

2. Механический – вся совокупность разбивается на равные по объёму группы по случайному признаку, затем из каждой группы берётся одна единица.

3. Типический – совокупность разбивается по существенному типическому признаку на качественно однородные группы, затем из каждой группы выделяется количество единиц пропорционально удельному весу группы. Типический отбор даёт более точные результаты, чем случайный и механический.

4. Серийный (гнездовой) – отбору подлежат не отдельные единицы совокупности, а целые группы (серии, гнёзда), отобранные случайным и механическим способами. В каждой группе проводится сплошное наблюдение, а результаты переносятся на всю совокупность.

Точность выборки зависит и от схемы отбора. Выборка может быть проведена по схеме повторного и бесповторного отбора.

Повторный отбор – каждая отобранная единица и серия возвращается во всю совокупность и может вновь попасть в выборку, что представляет собой схему “возвращённого шара”.

Бесповторный отбор – каждая обследованная единица изымается и не возвращается в совокупность, что даёт более точные результаты по сравнению с повторным отбором, т.к. при одном и том же объёме выборки охватывается большее количество единиц обследуемой совокупности.

Количество отобранных единиц обычно определяется, исходя из принятой доли выборки.

Доля выборки - отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности.

Применяя выборочный метод в статистике, обычно используют два основных вида обобщающих показателей:

1. Среднюю величину количественного признака;

2. Относительную величину альтернативного признака (долю или удельный вес единиц, которые отличаются от всех других единиц данной совокупности только наличием изучаемого признака).

Выборочная доля (ω''омега’’ − частость) определяется отношением числа единиц, обладающих изучаемым признаком (m) к общему числу единиц выборочной совокупности (n): .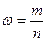

Ошибка выборки (E) представляет собой разность соответствующих выборочных и генеральных характеристик.

Для средних количественного признака: .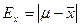

Для доли альтернативного признака: .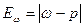

Конечной целью выборочного наблюдения является характеристика генеральной совокупности на основе полученных результатов.

Выборочные средние и относительные величины распространяются на генеральные совокупности с учётом предела их возможной ошибки.

Фактические расхождения, т.е. разница между выборочной средней и генеральной средней, могут рассматриваться как некая предельная ошибка, связанная со средней ошибкой и гарантированная с определённой вероятностью P.

P = Ф(t), где t – коэффициент доверия.

t	1,0	1,96	2,0	2,58
P = Ф(t)	0,683	…	0,954	…	0,997

Для стабильного процесса t =2, для нестабильного процесса t =3.

Предельная ошибка выборки позволяет определить предельные значения характеристик выборки и их доверительные интервалы:

;

, .

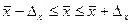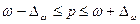Дата добавления: 2014-01-07