Использование показателей вариации в анализе взаимосвя­зей

Показатели вариации могут быть использованы не только в анализе колеблемости или изменчивости изучаемого признака, но и для оценки степени воздействия одного признака на вариацию другого признака, т.е. в анализе взаимосвязей между показателями.

При проведении такого анализа исходная совокупность должна пред­ставлять собой множество единиц, каждая из которых характеризуется двумя признаками - факторным и результативным. Факторным называет­ся признак, оказывающий влияние на взаимосвязанный с ним признак. В свою очередь, этот второй признак, подверженный влиянию, называется результативным.

Для выявления взаимосвязи исходная совокупность делится на две или более групп по факторному признаку. Выводы о степени взаимосвязи базируются на анализе вариации результативного признака. При этом применяется правило сложения дисперсий:

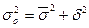(7.8.)

где 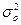- общая дисперсия;

- средняя из внутригрупповых дисперсий;

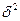- межгрупповая дисперсия.

Межгрупповая дисперсия отражает ту часть вариации результативного признака, которая обусловлена воздействием признака факторного. Это воздействие проявляется в отклонении групповых средних от общей средней:

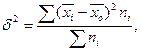(7.9.)

где - среднее значение результативного признака по i-ой группе;

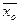- общая средняя по совокупности в целом;

- объем (численность) i-ой группы.

Если факторный признак, по которому производилась группиров­ка, не оказывает никакого влияния не признак результативный, то груп­повые средние будут равны между собой и совпадут с общей средней. В этом случае межгрупповая дисперсия будет равна нулю.

Средняя из внутригрупповых дисперсий отражает ту часть вариа­ции результативного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществля­лась группировка:

(7.10.)

где - дисперсия результативного признака в i-ой группе;

- объем (численность) i-ой группы.

Теснота связи между факторным и результативным признаком оценивается на основе эмпирического корреляционного отношения:

(7.11.)

Данный показатель может принимать значение от 0 до 1. Чем ближе к 1 будет его величина, тем сильнее взаимосвязь между рассматриваемыми признаками.

На следующем условном примере исследуем зависимость между собственными и привлеченными средствами коммерческих банков региона:

Таблица 7.2.

Банк	Собственные средства, млн. руб.	Привлеченные средства, млн. руб.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.

Если взаимосвязь между рассматриваемыми показателями существу­ет, то она обусловлена влиянием объема собственных средств на объем привлеченных средств. Поэтому объем собственных средств выступает в данном примере в качестве факторного признака (X), а объем привле­ченных средств в качестве результативного признака (Y).

Произведем группировку банков, выделив две группы по величине собственных средств, например, группу "да 100 млн. руб." и группу "100 млн. руб. и более". Результаты такой группировки представлены в сле­дующей таблице:

Таблица 7.3.

№ группы	Собственные средства, млн. руб.	Привлеченные средства, млн. руб.
1.	до 100	300 400 255 320 240 355
2.	100 и более	530 470 650 405

Расчет эмпирического корреляционного отношения включает несколько этапов:

1) рассчитываем групповые средние:

где i – номер группы;

j – номер единицы в группе.

млн. руб.;

млн. руб.

В данном примере при расчете групповых средних мы использовали невзвешенные формулы. Однако, при повторении вариантов для расчета необходимо использовать средние взвешенные.

2) рассчитываем общую среднюю:

млн. руб.

Данную среднюю также можно было получить как соотношение суммы всех единиц исходной совокупности (без учета деления на группы) к объему всей совокупности, т.е. к общему числу единиц.

3) рассчитываем внутригрупповые дисперсии:

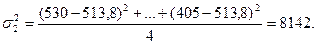
Если бы варианты имели веса, то для расчета внутригрупповых дисперсий также требовались бы взвешенные формулы.

4) вычисляем среднюю из внутригрупповых дисперсий:

5) определяем межгрупповую дисперсию:

находим общую дисперсию по правилу сложения:

На этом этапе возможна проверка правильности выполненных ранее расчетов. Если возвратиться к исходной совокупности и не раздета ее на группы рассчитать дисперсию признака «у», то она должна совпасть с общей дисперсией, полученной по правилу сложения.

Рассчитаем эмпирическое корреляционное отношение:

Полученная величина свидетельствует о том, что фактор, положенный в основание группировки (собственные средства), существенно влияет на размер привлеченных банками средств.

Дата добавления: 2014-01-07