Основные способы формирования выборочной совокупности

Достоверность рассчитанных по выборочным данным характери­стик в значительной степени определяется репрезентативностью выбо­рочной совокупности, которая, в свою очередь, зависит от способа отбо­ра единиц из генеральной совокупности. В каждом конкретном случае в зависимости от целого ряда условий, а именно, сущности исследуемого явления, объема совокупности, вариации и распределения наблюдаемых признаков, материальных и трудовых ресурсов, выбирают наиболее предпочтительную систему организации отбора, которая определяется видом, методом и способом отбора.

По виду различают индивидуальный, групповой и комбинирован­ный отбор. При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной совокупности, при груп­повом отборе - группы единиц, а комбинированный отбор предпола­гает сочетание группового и индивидуального отбора.

Метод отбора определяет возможность продолжения участия отобранной единицы в процедуре отбора.

Бесповторным называется отбор, при котором попавшая в вы­борку единица не возвращается в совокупность, из которой осуществля­ется дальнейший отбор.

При повторном отборе попавшая в выборку единица после реги­страции наблюдаемых признаков возвращается в исходную (генераль­ную) совокупность для участия в дальнейшей процедуре отбора. Повторный метод отбора применяется в тех случаях, когда характер иссле­дуемого явления предполагает возможность повторной регистрации единиц- Такая возможность, прежде всего, может иметь место в выборочных обследованиях населения в качестве покупателей, пациентов, избирателей, абитуриентов и т.д.

Способ отбора определяет конкретный механизм или процедуру выборки единиц из генеральной совокупности. В практике выборочных обследований наибольшее распространение получили следующие виды выборки:

• собственно-случайная;

• механическая;

• типическая;

• серийная;

• комбинированная.

Собственно-случайная выборка заключается в отборе единиц из генеральной совокупности наугад или наудачу без каких-либо элементов системности. Однако прежде чем производить собственно-случайный отбор, необходимо убедиться, что все без исключения единицы гене­ральной совокупности имеют абсолютно равные шансы попадания в вы­борку, в списках или перечне отсутствуют пропуски, игнорирования от­дельных единиц и т.п. Следует также установить четкие границы гене­ральной совокупности таким образом, чтобы включение или не включение в нее отдельных единиц не вызывало сомнений. Так, например, при обследовании студентов необходимо указать, будут ли приниматься во внимание лица, находящиеся в академическом отпуске, студенты него­сударственных вузов, военных училищ и т.п.; при обследовании торго­вых предприятий важно определиться, включит ли генеральная сово­купность торговые павильоны, коммерческие палатки и прочие подоб­ные объекты.

Технически собственно-случайный отбор проводят методом жеребь­евки или по таблице случайных чисел.

Для жеребьевки необходимо подготовить достаточное количество жребиев - фишек, шаров, карточек, соответствующее объему генераль­ной совокупности. Каждый жребий должен содержать информацию об отдельной единице совокупности - номер, фамилию лица или адрес, на­звание или какой-либо другой отличительный признак. Необходимое в соответствии с установленным процентом отбора количества жребиев извлекается из общей их совокупности в случайном порядке.

При отборе по таблицам случайных чисел каждая единица генераль­ной совокупности должна иметь порядковый номер. Таблицы случайных чисел получаются с помощью датчика случайных чисел на ПК и пред­ставляют собой абсолютно произвольные столбцы цифр. В соответствии с объектом генеральной совокупности выбирается любой столбец с чис­лами необходимой значимости. Например, если генеральная совокуп­ность включает 5000 единиц, потребуется четырехзначные столбцы, при этом числа больше 5000 не будут приниматься во внимание. В выбороч­ную совокупность отбираются единицы с порядковыми номерами, соответствующими числам выбранного столбца.

Собственно-случайный отбор может быть как повторным, так и бесповторным. Для проведения бесповторного отбора в процессе жеребьев­ки выпавшие жребии обратно в исходную совокупность не возвращают­ся и в дальнейшем отборе не участвуют. При использовании таблиц слу­чайных чисел бесповторность отбора достигается пропуском чисел в случае их повторения в выбранном столбце или столбцах.

После проведения отбора для определения возможных границ генеральных характеристик рассчитываются средняя и предельная ошибки выборки.

Эти два вида ошибок связаны следующим соотношением:

где ∆ - предельная ошибка выборки;

µ - средняя ошибка выборки;

t – коэффициент доверия, определяемый в зависимости от уровня вероятности p.

Ниже приведены некоторые значения t.

Таблица 8.2.

Вероятность	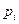0,683	0,866	0,954	0,988	0,997	0,999
Значение t	1,0	1,5	2,0	2,5	3,0	3,5

Величина средней ошибки выборки рассчитывается дифференцированно в зависимости от способа отбора и процедуры выборки. Так, при случайном повторном отборе средняя ошибка определяется по формуле:

,

а при бесповторном:

где 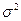- выборочная (или генеральная) дисперсия;

σ – выборочное (или генеральное) среднее квадратическое отклонение;

n – объем выборочной совокупности;

N – объем генеральной совокупности.

Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности. Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений:

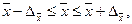
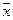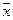где и - генеральная и выборочная средняя соответственно;

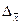- предельная ошибка выборочной средней.

Покажем практическое применение рассмотренной выше методики на следующих примерах.

Пример 1. При проверке веса импортируемого груза на таможне ме­тодом случайной повторной выборки было отобрано 200 изделий. В ре­зультате был установлен средний вес изделия 30 г. при среднем квадратическом отклонении 4 г. С вероятностью 0,997 определите пределы, в которых находится средний вес изделия в генеральной совокупности.

Решение. Рассчитаем сначала предельную ошибку выборки. Так как при p = 0,997 t = 3, она равна:

Определим пределы генеральной средней:

или

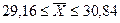
Следовательно, с вероятностью 0,997 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 29,16 г. до 30,84 г.

Пример 2. В городе проживает 250 тыс. семей. Для определения среднего числа детей в семье была организована 2%-ная случайная бесповторная выборка семей. По ее результатам было получено следующее распределение семей по числу детей:

Число детей в семье
Количество семей

С вероятностью 0,954 определите пределы, в которых будет находиться среднее число детей в генеральной совокупности.

Решение. Вначале на основе имеющегося распределения семей определим выборочные среднюю и дисперсию:

Число детей в семье,	Количество семей,
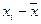
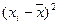
			-1,5 -0,5 0,5 1,5 2,5 3,5	2,25 0,25 0,25 2,25 6,25 12,25
Итого			-	-

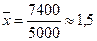(чел.);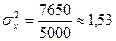

Вычислим теперь предельную ошибку выборки (с учетом того, что при p = 0,954 t = 2).

Следовательно, пределы генеральной средней:

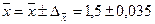
Таким образом, с вероятностью 0,954 можно утверждать, что среднее число детей в семьях города практически не отличается от 1,5, т.е. в среднем на каждые две семьи приходится три ребенка.

Наряду с определением ошибок выборки и пределов для генераль­ной средней эти же показатели могут быть определены для доли призна­ка. В этом случае особенности расчета связаны с определением диспер­сии доли, которая вычисляется так:

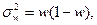
где - доля единиц, обладающих данным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки.

Тогда, например, при собственно-случайном повторном отборе для определения предельной ошибки выборки используется следующая формула:

Соответственно, при повторном отборе:

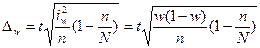
Пределы доли признака в генеральной совокупности p выглядят следующим образом:

Рассмотрим пример.

Пример 3. С целью определения средней фактической продолжительности рабочего дня в государственном учреждении с численностью служащих 480 человек, в январе 200а г. была проведена 25%-ная случайная бесповоротная выборка. По результатам наблюдения оказалось, что у 10% обследованных потери времени достигали более 45 мин. в день. С вероятностью 0,683 установите пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 мин. в день.

Решение. Определим объем выборочной совокупности:

n = 480 × 0,25 = 120 чел.

Выборочная доля w равна по условию 10%.

Учитывая, что при p = 0,683 t = 1, вычислим предельную ошибку выборочной доли:

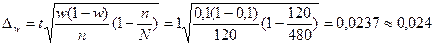или 2,4%

Пределы доли признака в генеральной совокупности:

или

Таким образом, с вероятностью 0,683 можно утверждать, что доля работников учреждения с потерями рабочего времени более 45 мин. в день находится в пределах от 7,6% до 12,4%.

Механическая выборка применяется в случаях, когда генераль­ная совокупность каким-либо образом упорядочена, т.е. имеется опреде­ленная последовательность в расположении единиц (табельные номера работников, списки избирателей, телефонные номера респондентов, но­мера домов и квартир и т.п.).

Для проведения механической выборки устанавливается пропор­ция отбора, которая определяется соотнесением объемов выборочной и генеральной совокупностей. Так, если из совокупности в 500 000 единиц предполагается получить 2%-ную выборку, т.е. отобрать 10 000 единиц, то пропорция отбора составит 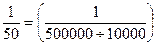. Отбор единиц осуществляется в соответствии с установленной пропорцией через равные интервалы. Например, при пропорции 1:50 (2%-ная выборка) отбирается каждая 50-я единица, при пропорции 1:20 (5%-ная выборка) – каждая 20-я единица и т.д.

Генеральную совокупность при механическом отборе можно ранжировать или упорядочить по величине изучаемого или коррелирующего с ним признака, что позволит повысить репрезентативность выборки. Однако в этом случае возрастает опасность систематической ошибки, связанной с занижением значений изучаемого признака (если из каждого интервала регистрируется первое значение) или с его завышением (если из каждого интервала регистрируется последнее значение). Поэтому целесообразно отбор начинать с середины первого интервала, например, при 5%-ной выборке отобрать 10-ю, 30-ю, 50-ю, 70-ю и с таким же интервалом последующие единицы.

Для определения средней ошибки механической выборки исполь­зуется формула средней ошибки при собственно-случайном бесповтор­ном отборе.

Типический отбор. Этот способ отбора используется в тех случа­ях, когда все единицы генеральной совокупности можно разбить на не­сколько типических групп. При обследовании населения такими груп­пами могут быть, например, районы, социальные, возрастные или образовательные группы, при обследовании предприятий - отрасль или под­отрасль, форма собственности и т.п. Типический отбор предполагает выборку единиц из каждой типической группы собственно-случайным или механическим способом. Поскольку в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, типизация генеральной совокупности позволяет исключить влия­ние межгрупповой дисперсии на среднюю ошибку выборки, которая в этом случае определяется только внутригрупповой вариацией.

Отбор единиц в типическую выборку может быть организован ли­бо пропорционально объему типических групп, либо пропорционально внутригрупповой дифференциации признака.

При выборке, пропорциональной объему типических групп, число единиц, подлежащих отбору из каждой группы, определяется следую­щим образом:

,

где - объем i-ой группы;

- объем выборки за i-ой группы.

Средняя ошибка такой выборки находится по формулам:

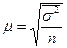(повторный отбор)

(бесповторный отбор)

где - средняя из внутригрупповых дисперсий.

При выборке, пропорциональной дифференциации признака, число наблюдений по каждой группе рассчитывается по формуле:

,

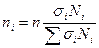где 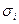- среднее квадратическое отклонение признака в i-ой группе.

Средняя ошибка такого отбора определяется следующим образом:

(повторный отбор)

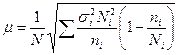(бесповторный отбор)

Отбор, пропорциональный дифференциации признака, дает луч­шие результаты, однако на практике его применение затруднено вслед­ствие трудности получения сведений о вариации до проведения выбо­рочного наблюдения.

Рассмотрим оба варианта типической выборки на условном при­мере. Предположим, 10% бесповторный типический отбор рабочих предприятия, пропорциональный размерам цехов, проведенный с целью оценки потерь из-за временной нетрудоспособности, привел к следую­щим результатам (табл. 8.3.).

Таблица 8.3.

Дата добавления: 2014-01-07