Оценка результатов выборочного наблюдения и распростра­нение их на генеральную совокупность

Заключительным этапом выборочного наблюдения является рас­пространение его результатов на генеральную совокупность. Однако часто при статистическом изучении социально-экономических явлений этому процессу предшествует оценка результатов наблюдения с точки зрения самой возможности распространения.

Вывод о возможности распространения в значительной степени зависит от качества основы выборки, прежде всего от ее полноты. Под полнотой подразумевается наличие или представленность всех типов или групп данной генеральной совокупности в основе выборки. Неполнота основы может привести к нарушению представительности выборки и, как следствие, к неправильным выводам при анализе данных наблю­дения.

Однако не следует обосновывать возможность распространения выборочных данных только анализом качества исходной информации для отбора. Более точной основой суждения о возможности распростра­нения представляется расчет относительной ошибки:

для средней: ,

для доли: ,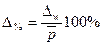

где 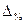- относительная предельная ошибка выборк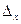и;

и 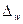- предельная ошибка для среднего значения или доли признака соответственно;

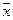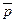и - генеральная средняя и доля соответственно.

Суждение о возможности распространения выборочных данных можно составить, если в формулах заменить 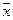и 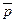соответствующими выборочными характеристиками. Необходимым условием при этом яв­ляется соответствие плановой и фактической численности и структуры выборочной совокупности. При больших расхождениях использование этого приема может привести к ошибочным суждениям.

Если величина относительной ошибки не превышает заранее уста­новленного для данного обследования предельного значения, то данные выборочного наблюдения являются представительными и могут быть распространены на генеральную совокупность.

Существуют два основных метода распространения - прямой пе­ресчет и способ коэффициентов.

Сущность способа прямого пересчета заключается в умножении среднего значения признака, найденного в результате выборочного на­блюдения, на объем генеральной совокупности. Практические расчеты при этом не вызывают серьезных затруднений. Например, на основании выборочного обследования 1000 молодых семей требуется оценить по­требность в местах в детских яслях. С помощью метода прямого пересчета это можно сделать следующим образом. Известно, что ясли могут посещать дети в возрасте до трех лет. По материалам выборочного об­следования следует вычислить среднее число детей этого возраста в рас­чете на 1 семью. Предположим, что оно составляет 0,3 человека. Умно­жив это число на численность генеральной совокупности, получим, что в детских яслях потребуется выделить 300 мест.

В условиях существования большого числа факторов, влияющих на точность данных выборочного наблюдения, использование точечной оценки при распространении выборочных характеристик на генераль­ную совокупность в статистических исследованиях часто нецелесообразно. Во всех случаях, когда это возможно, правильнее пользоваться интервальной оценкой, позволяющей учесть размер предельной ошибки выборки, рассчитанной для средней или для доли признака. Так, если в нашем примере число детей в возрасте до трех лет по выборочным дан­ным составило 0,3 человека, а предельная ошибка - ± 0,1 человека, то требуемое количество мест в детских учреждениях будет находиться в пределах от 200 до 400.

Наряду со способом прямого пересчета при распространении дан­ных выборочного наблюдения на генеральную совокупность применяет­ся так называемый способ коэффициентов. Данный способ целесооб­разно использовать в случаях, когда выборочное наблюдение проводит­ся с целью проверки и уточнения данных сплошного наблюдения, в ча­стности численности учтенных единиц совокупности.

При этом следует использовать следующую формулу:

,

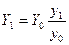где Y - численность совокупности с поправкой на недоучет;

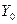- численность совокупности без этой поправки;

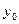- численность совокупности в контрольных точках по первона­чаль­ным данным;

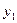- численность совокупности в тех же точках по данным контроль­ных мероприятий.

До сих пор возможности выборки при уточнении данных сплош­ного наблюдения используются недостаточно. В то же время в совре­менных условиях данный способ может быть, например, одним из инструментов контроля деятельности коммерческих структур со стороны финансовых органов.

При уточнении данных сплошного наблюдения на основе кон­трольных выборочных мероприятий определяется так называемая по­правка на недоучет. Метод ее расчета наиболее широко применяется в обследованиях относительно небольших совокупностей, когда их объем не превышает нескольких сотен или тысяч единиц.

Пример 8. При проведении учета коммерческих палаток в городе было зарегистрировано следующее их количество в районах: А - 2000; Б - 1500; В - 750. С целью проверки данных сплошного учета проведены контрольные обходы части обследованных районов. Их результаты содержатся в нижеприведенной табл. 7.4.

Таблица 8.4.

Дата добавления: 2014-01-07