Оценка линейного коэффициента корреляции

Значение линейного коэффициента связи	Характер связи	Интерпретация связи
r = 0	отсутствует	-
0<r<1	прямая	с увеличением x увеличивается y
-1<r<0	обратная	с увеличением x уменьшается y и наоборот
r = 1	функциональная	каждому значению факторного признака строго соответствует одно значение результативного признака

Пример: На основе выборочных данных о деловой активности однотипных коммерческих структур оценить тесноту связи между прибылью y (млн. руб.) и затратами на 1 руб. произведенной продукции x (коп.).

Таблица 9.6.

Расчетная таблица для определения коэффициента корреляции

№ п/п	y	x	yx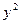
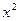
Сумма
Средняя	744,33	83,67	60400,67	632056,33	7046,67

1. Используя формулу (9.5.) получаем:

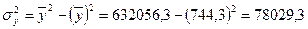
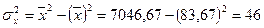
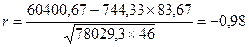
2. По формуле (9.6.) значение коэффициента корреляции составило:

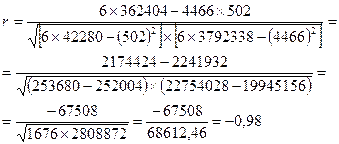
Таким образом, результат по всем формулам одинаков и свиде­тельствует о сильной обратной зависимости между изучаемыми призна­ками.

В случае наличия линейной и нелинейной зависимости между двумя признаками для измерения тесноты связи применяют так назы­ваемое корреляционное отношение. Различают эмпирическое и теоре­тическое корреляционное отношение.

Эмпирическое корреляционное отношение рассчитывается по данным группировки, когда 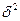характеризует отклонения групповых средних результативного показателя от общей средней:

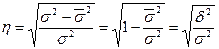(9.8.)

где 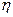- корреляционное отношение;

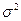- общая дисперсия;

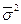- средняя из частных (групповых) дисперсий;

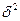- межгрупповая дисперсия (дисперсия групповых средних).

Все эти дисперсии есть дисперсии результативного признака.

Теоретическое корреляционное отношение определяется по формуле:

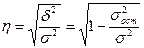(9.9.)

где 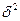- дисперсия выравненных значений результативного признака, то есть рассчитанные по уравнению регрессии;

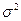- дисперсия эмпирических (фактических) значений результативного признака.

Корреляционное отношение изменяется в пределах от 0 до 1 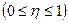и анализ степени тесноты связи полностью соответствует линейному коэффициенту корреляции (таблица 9.1.)

Для измерения тесноты связи при множественной корреляционной зависимости, то есть при исследовании трех и более признаков одновременно, вычисляется множественный и частные коэффициенты корреляции.

Множественный коэффициент корреляци и вычисляется при наличии линейной связи между результативным и несколькими фактор­ными признаками, а также между каждой парой факторных признаков.

Множественный коэффициент корреляции для двух факторных признаков вычисляется по формуле:

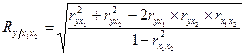(9.10.)

где 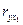- парные коэффициенты корреляции между признаками.

Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен: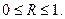

Приближение R к единице свидетельствует о сильной зависимости между признаками.

На основе данных таблицы 9.4. рассчитаем коэффициент множественной корреляции и его ошибку:

; ; .

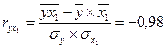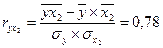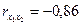Множественный коэффициент корреляции составит:

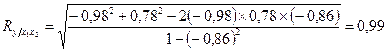
Частные коэффициенты корреляции характеризуют степень тесноты связи между двумя признакам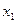и и 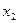при фиксированном значении других (k – 2) факторных признаков, то есть когда влияние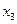исключается, то есть оценивается связь между 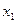и 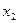в «чистом виде».

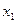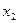В случае зависимости y от двух факторных признаков и коэффициенты частной корреляции имеют вид:

; .

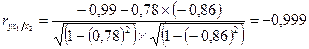
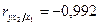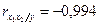Дата добавления: 2014-01-07