Расчет коэффициента Спирмена

№ предприятия	Уставный капитал (млн. руб.) (X)	Число выставленных акций (Y)	Ранги	Разность рангов
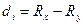
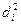
					-8 -5
∑

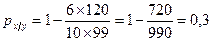(связь слабая).

Ранговый коэффициент корреляции Кендалла 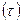также сожжет использоваться для измерения взаимосвязи между качественными и количественными признаками, характеризующими однородные объекты и ранжированные по одному принципу. Расчет рангового коэффициента Кендалла осуществляется по формуле:

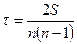(9.20.)

где n – число наблюдений;

S – сумма разностей между числом последовательностей и числом инверсий по второму признаку.

Расчет данного коэффициента выполняется в следующей последовательности:

1. Значения X ранжируются в порядке возрастания или убывания.

2. Значения Y располагаются в порядке, соответствующем значениям X.

3. Для каждого ранга Y определяется число следующих за ним значений рангов, превышающих его величину. Суммируя таким образом числа определяется величина P, как мера соответствия последовательностей рангов по X и Y и учитывается со знаком (+).

4. Для каждого ранга Y определяется число следующих за ним значений рангов, меньших его величины. Суммарная величина обозначается через Q и фиксируется со знаком (-).

5. Определяется сумма баллов по всем членам ряда.

В приведенном примере (таблица 9.12.)

P=1+8+1+6+4+3+3+2+1=29

Q=(-8)+0+(-6)+0+(-1)+(-1)+0+0+0= -16

Таким образом:

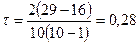
что свидетельствует о практическом отсутствии связи между рассматриваемыми признаками.

Как правило, коэффициент Кендалла меньше коэффициента Спирмена. При достаточно большом объеме совокупности значения Данных коэффициентов имеют следующую зависимость:

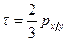
Связь между признаками признается статистически значимой, ес­ли значения коэффициентов ранговой корреляции Спирмена и Кендалла больше 0,5.

Для определения тесноты связи между произвольным числом ранжированных признаков применяется множественный коэффициент ранговой корреляции (коэффициент конкордации) W, который вычисляется по формуле:

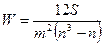(9.21.)

где m – количество факторов;

n – число наблюдений;

S – отклонение суммы квадратов рангов от средней квадратов рангов.

Пример. Одновременно с проведенными выше расчетами определялась теснота связи между уставным капиталом, числом выставленных акций и числом занятых на этих предприятиях.

Таблица 9.13.

Дата добавления: 2014-01-07