Назначение и способы построения провероч­ной матрицы циклического кода

Проверочные матрицы H_l,n(x) ЦК могут использоваться для выбора как способов кодирования информации, так и алгоритмов декодирования. Проверочные матрицы ЦК могут быть построены с использованием порождающей матрицы G_k,n(x), е диничной матрицы проверок и проверочного полинома h(x).

Сущность способа построения проверочной матрицы Н_{l, n}(x) c использованием канонической порождающей матрицы G_k,n(x) состоит в следующем.

Пусть задана следующая каноническая порождающая матрица ЦК с параметрами (n,k,do)=(7,4,3) вида:

1000 101

G_4,7(x) = 0100 111

0010 110

0001 011

Первый столбец проверочной матрицы Н_3,7(х) для данного кода записываем, используя проверочные символы первой строки G_4,7(x), а второй, третий и четвертый столбцы H_3,7(x) формируем путем записи проверочных символов второй, третьей и четвертой строк G_4,7(x) и далее записываем три столбца единичной подматрицы. В результате получаем следующую проверочную матрицу:

а₁а₂а₃а₄ b₁b₂b₃

1110 100

H_3,7(x) = 0111 010

1101 001

Ненулевые символы строк проверочной матрицы определяют позиции информационных символов, участвующие в формировании проверочных уравнений. Так для построенной проверочной матрицы H_3,7(x) можно сформировать следующие три проверочных уравнения: b₁= а₁Åa₂Åa₃, b₂= а₂Åa₃Åa₄, b₃= а₁Åa₂Åa_4.

Принцип построения проверочной матрицы с использова­нием единичной подматрицы и остатков от деления аналогичен принципу построения порождающей матрицы. Количество ос­татков от деления х^п+1 на Р(х) должно быть равно количеству строк единичной подматрицы.

Сущность принципа построения проверочной матрицы ЦК с использованием проверочного полинома h(x) состоит в следующем. Первоначально определяем проверочный полином как отношение х^п+1 на Р(х), т.е. 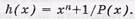Полученный полином переводим в двоичную форму записи, записываем в виде первой строки проверочной матрицы Н_l,k(х) и дополняем нулями до количества столбцов, равное п. Далее выполняем (l-1) циклический сдвиг двоичных символов пер­вой строки.

Пример: Построить проверочную матрицу ЦК с пара­метрами

Решение:

1) определяем проверочный полином

2) переводим h(x) в двоичную форму записи h(x) – 11101;

3) записываем 11101 в виде первой строки Н_3,7(х) и дополняем справа двумя нулевыми символами до n=7;

4) выполняя (l - 1)=(3-1)=2 циклических сдвига двоичных символов первой строки Н_3,7(х) строим проверочную матрицу Н_3.7(х) следующего вида:

Проверочные уравнения: b₁= а₁Åa₂Åa₃,

b₂= а₂Åa₃Åa₄,

b₃= а₃Åa₄Åb₁= а₃Åa₄Å а₁Åa₂Åa₃= а₁Åa₂Åa_4.

Дата добавления: 2014-01-07