Краткие сведения о принципах действия дискретных и цифровых фильтров

Недостатки аналоговых фильтров. Рассмотренные в гл. 5 аналоговые фильтры обладают рядом недостатков, в том числе: 1) трудности обеспечения высокой стабильности частоты настройки и 2) формы частотных характеристик в связи с тем, что параметры элементов фильтров (конденсаторов, катушек индуктивности, резисторов и т.п.) изменяются под воздействием температуры, влаги, механических нагрузок и во времени; 3) резко выраженная зависимость габаритов, массы и стоимости от частоты (при низких частотах); 4) необходимость точной механической обработки (электромеханические и кварцевые фильтры); 5) трудность получения высокой добротности (LC -фильтры и активные RC -фильтры); 6) существенные ограничения в области высоких частот.

Эти недостатки обуславливаются трудностями обеспечения: 1) требуемого резонансного сопротивления при малых индуктивностях в LC -фильтрах, 2) ограничением по высшей частоте операционных усилителей в RC -фильтрах, 3) сложностью создания электромеханических и кварцевых резонаторов малых размеров. Поэтому аналоговые фильтры не могли решить многие задачи фильтрации в РЭА и необходимо было создать фильтры на новых принципах. Такими фильтрами являются дискретные и цифровые.

Для объяснения свойств и возможностей дискретных и цифровых фильтров удобно использовать отображение сигнала и его смеси с помехой в выборке отсчетов (значений), взятых через дискретные интервалы времени t_вб, а также квантование отсчетов. В основу цифровой передачи и записи аналоговых сигналов положена импульсно-кодовая модуляция (ИКМ). Она обеспечивает дискретизацию (квантование) и кодирование.

Цифровая запись. Рис. 1. Схема импульсно-кодовой модуляции (ИКМ) аналогового сигнала и его восстановление из ИКМ – сигнала:

а – исходный аналоговый сигнал u(t) с выделенными дискретными значениями (отсчетами), – интервал дискретизации;

б – последовательность отсчетов, округленных до ближайшего из уровней квантования ±х_n; ∆х – шаг квантования; 0000, 0001, 0010, 0011 – четырехзначные кодовые слова, соответствующие выбранным уровням квантования;

в – ИКМ - сигнал;

г – восстановление из ИКМ – сигнала отсчета и аналоговый сигнал.

Рис.1

Рис. 2. Структурная схема и временные диаграммы цифрового фильтра: УД – устройство дискретизации, преобразующее аналоговый сигнал x(t) в последовательность импульсов (решетчатую функцию) x*(t); АЦП – аналого-цифровой преобразователь, с помощью которого мгновенные значения аналогового сигнала заменяются ближайшими дискретными уровнями X(nT), где n=0, 1, 2…, T – период следования импульсов, ВУ – вычислительное устройство, преобразующее последовательность чисел (уровней) X(nT) в выходную функцию Y(nT); ЦАП – цифро-аналоговый преобразователь, в котором Y(nT) преобразуется в выходной аналоговый сигнал y(t).

Если оперировать с выборкой, то можно осуществлять фильтрацию, обрабатывая отсчеты выборки, т.е. построить фильтр так, чтобы он действовал не непрерывно, а в моменты времени через t_вб. Это позволило создать дискретные (по времени) фильтры, техническая реализация которых основывается на принципах, отличающихся от используемых в аналоговых.

От дискретных фильтров можно перейти к цифровым.

Напомним, что для анализа и расчета аналоговых фильтров обычно используется частотная область, т.е. спектры сигналов и частотные характеристики фильтров. Для дискретных и цифровых фильтров также могут использоваться дискретные характеристики, но для понимания их принципа действия удобнее пользоваться временной областью, т.е. рассматривать их работу во времени.

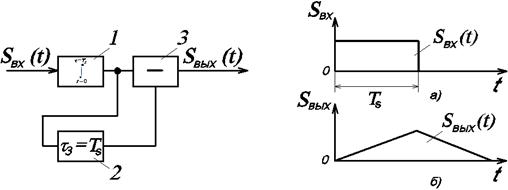
Рис. 3 Рис. 4

Рис. 3. Оптимальный фильтр для прямоугольного видеоимпульса – аналоговый и линейный 1 – интегратор; 2 – задержка; 3 – устройство вычитания.

Рис. 4. а – прямоугольный сигнал на входе и его отклик на выходе (б), т.к. сигнал проходит…

Помеха при интегрировании частично компенсируется (значения помехи имеют разные знаки).

Сущность фильтрации: накопление отклика на сигнал, чем длительнее накопление, тем больше отношение сигнал/помеха на выходе фильтра.

Так работают аналоговые фильтры.

Принцип действия дискретного фильтра. Поскольку в устройствах фильтрации осуществляется накопление информации, то для получения эффекта фильтрации можно использовать не только явление резонанса. Дискретный фильтр действует не непрерывно, а дискретно обрабатывает отсчеты значений сигнала, взятые через интервал времени. Для накопления или суммирования таких сигналов можно применить дискретный накопитель с сумматором. Простейшим видом такого устройства является линия задержки на элементах LC с отводами, напряжения с которых подаются на сумматор.

Принцип построения такой линии иллюстрируется рис. 6.4, где 1 – линии задержки (показан простейший вариант из элементов L и C); 2 – отводы; 3 – резисторы (подбирая их сопротивления, можно изменять “вклад” отвода в сумму); 4 – сумматор в виде общего сопротивления R_∑, обеспечивающий совместное использование сигналов, накапливаемых в линии задержки.

Для простоты полагаем, что сопротивления в отводах одинаковые, и посмотрим, как сигнал в виде прямоугольного импульса пройдет через такой дискретный фильтр (рис. 6.5).

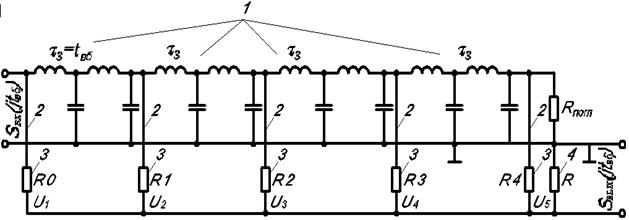
Рис. 6.4

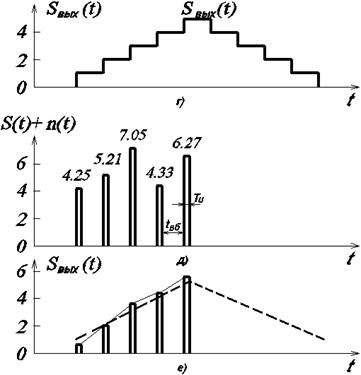
Рис. 6.5

На рис. 6.5, а показан сигнал S(t) c прямоугольной огибающей длительностью T_s; n(t) – помеха. На рис. 6.5, б – выборка из сигнала в виде пяти отсчетов, длительность импульсов выборки T_и; t_вб – интервал выборки. На рис. 6.5, в – отклик на выходе линии задержки, содержащей пять отводов, с которых сигналы подаются на общий сумматор (масштаб изменен по отношению к рис. 6.5, б в 2 раза). Этот отклик представляет собой сумму отсчетов выборки и подобен отклику, показанному на рис. 6.2, но является дискретным во времени. Поскольку линия задержки представляет набор дискретных звеньев с отводами, то процесс дискретизации во времени может происходить непосредственно в ней.

На рис. 6.5, г показан вид отклика на сигнал на выходе фильтра S_вых(t), если подать на такой дискретный фильтр сигнал, не осуществляя выборки (масштаб изменен по отношению к рис. 6.5, б в 5 раз).

Из рис. 6.5, д можно видеть, что если сигнал на входе действует вместе с помехой, то отсчеты будут больше (помеха складывается с сигналом) или меньше (помеха вычитается из сигнала). На рис. 6.5, е видно, что в сумматоре произойдет частичная компенсация помех и они будут накапливаться медленнее, чем отклик на сигнал (масштаб изменен по отношению к рис. 6.5, б в 5 раз).

В приведенном примере при пяти отводах на выходе фильтра сигнал увеличивается в 5 раз. Помеха за счет компенсации возрастает на выходе примерно в 2 раза, и отношение сигнала к помехе улучшится примерно в 2 раза.

Реально сигналы сложнее, чем прямоугольный импульс, соответственно дискретные фильтры сложнее, чем показанный на рис. 6.4, но основной эффект выделения сигнала из помех при дискретном накоплении сохраняется. Следует обратить внимание на то, что фильтр получается значительно сложнее, чем простой фильтр RC; требуется большее количество элементов – катушек индуктивности и конденсаторов. Создание фильтров, основанных на изложенном принципе, практиковалось только для сложных сигналов (например, фазоманипулированных), так как дискретный характер таких сигналов требовал использования дискретного фильтра.

Дискретные фильтры стали широко применяться для сигналов только после того, как были созданы приборы с зарядовой связью (ПЗС) и приборы на поверхностных акустических волнах (ПАВ), где реализация звена задержки (памяти) неизмеримо проще, чем на электрических линиях задержки, показанных на рис. 6.4. Свойства дискретного фильтра с учетом его особенностей широко используются при изучении, синтезе и расчете цифровых фильтров. Действительно, как будет видно из изложенного ниже, в предположении, что интервал квантования выбран небольшим, числом разрядов в кодовых комбинациях достаточно большое, эффектами квантования и другими эффектами, связанными с ограниченным количеством разрядов, можно пренебречь. Тогда цифровой фильтр работает как дискретный. Таким образом, модель дискретного фильтра имеет определяющее значение в изучении, анализе и синтезе цифровых фильтров.

Принцип действия цифрового фильтра. Накопление, лежащее в основе фильтрации, может быть получено с использованием процедуры, связанной с суммированием, а суммирование является основной арифметической операцией. Следовательно, потенциально имеется возможность осуществления избирательных свойств в устройствах, производящих арифметические операции. Например в АЦП отсчеты, взятые в дискретные моменты времени квантуются и отображаются не в напряжении, а в виде числа, которое на выходе отображается кодом с конечным числом разрядов дискретных вторичных сигналов. Затем эти кодовые комбинации обрабатываются в цифровом фильтре.

Значение выборки отобразим пятиразрядным двоичным числом. Над взятыми 5 отсчетами будет выполняться операция последовательного суммирования 5 отсчетов, представленных в цифровой форме на рис. 6.6, а – смесь сигнала с помехой. Она соответствует рис. 6.5 для трехразрядного десятичного числа. Квантование округлит их до записи 4, 5, 7, 4, 6 (рис. 6.6, б), удерживается только старший (целый) разряд. Возникают помехи квантования. АЦП преобразовывает значения 4, 5, 7, 4, 6 в пятиразрядные числа (рис. 6.6, г).

При амплитуде сигнала 5, 5, 5, 5, 5 сумма=25. При амплитуде сигнала 4, 5, 7, 4, 6 с помехой сумма=26. Двоичный код на рис. 6.6, в. Процесс сложения показан на рис. 6.7.

Отклик в результате суммирования чисел 4, 5, 7, 4, 6 представлен в таблице, на шестом такте подается число 00000 и не читается последовательное исключение чисел без помехи и с помехой.

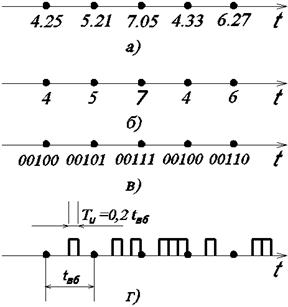
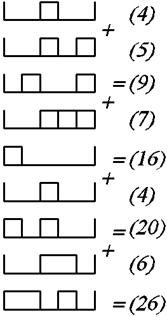
Рис. 6.6 Рис. 6.7

Таблица 6.1

Номер такта	Число, поступающее на вход без помехи	Сумма без помехи	Число, поступающее на вход с учетом помехи	Сумма с учетом помехи
	00101 (5) 00101 (5) 00101 (5) 00101 (5) 00101 (5)	00101 (5) 01010 (10) 01111 (15) 10100 (20) 11001 (25) 10100 (20) 01111 (15) 01010 (10) 00101 (5) 00000 (0)	00100 (4) 00101 (5) 00111 (7) 00100 (4) 00110 (6)	00100 (4) 01001 (9) 10000 (16) 10100 (20) 11010 (26) 10110 (22) 10001 (17) 01010 (10) 00110 (5) 00000 (0)

После получения суммы пяти чисел происходит процесс “вычитания”, так как на входе прекращается действие сигнала. Подается число 00000, а тактовые импульсы, управляющие действием сумматора, будут последовательно исключать из суммы в начале первое число, потом второе и т.д., как это показано, начиная с шестого такта, в табл. 6.1. В аппаратуре преобразование аналогового сигнала в цифровой происходит с помощью АЦП, выпускаемых промышленностью серийно.

Если необходимо от цифрового отклика вновь перейти к аналоговому, то используются серийно выпускаемые цифро-аналоговые преобразователи (ЦАП).

Используя принцип работы цифрового фильтра, фильтр может быть построен на различной элементной базе, например, …..

Раздел 3 АКУСТОЭЛЕКТРОНИКА

· Акустоэлектроника — направление функциональной микроэлектроники, связанное с использованием механических резонансных эффектов, пьезоэлектрического эффекта, а также эффекта, основанного на взаимодействии электрических полей с волнами акустических напряжений в пьезоэлектрическом полупроводниковом материале.

Акустоэлектроника занимается преобразованием акустических сигналов в электрические и электрических сигналов в акустические.

На принципе электромеханического резонанса основан прибор, называемый резонистором и представляющий собой транзистор с резонирующим затвором (рис. 9.15). Затвор З, представляющий собой часть балки, противоположный конец которой закреплен на изоляторе, нависает над каналом между стоком С и истоком И. Под балкой на изоляторе расположен электрод, на который подается входной сигнал. Сила электростатического взаимодействия сигнального электрода с затвором, на который

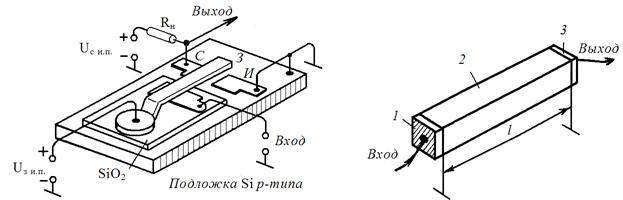
Рис. 9.15. Устройство резонистора

Рис. 9.16. Ультразвуковая линия задержки: 1 – входной преобразователь; 2 – звукопровод; 3 – выходной преобразователь

Υ

Тема 3.1. Акустоэлектронные приборы

Работа акустоэлектронных приборов основана на возбуждении, распространении и приеме акустических волн в твердых телах.

Использование в таких приборах акустических волн, распространяющихся по поверхности твердого тела, так называемых поверхностных акустических волн (ПАВ), предпочтительнее, чем волн, которые распространяются в объеме твердого тела. Поверхностно-акустические волны обладают меньшим по сравнению с объемными, затуханием и рассеиванием, позволяют отводить часть энергии с любого участка распространения ПАВ и управлять этими волнами электронным потоком. Кроме того, технология изготовления приборов на ПАВ хорошо совмещается с технологией изготовления микросхем. На основе акустоэлектронных приборов можно создать устройства, обладающие новыми функциями или существенно улучшить параметры уже известных устройств (частотной селекции и задержки сигналов).

Скорость распространения акустических волн в твердых телах в 10⁵ раз меньше скорости распространения электромагнитных волн в свободном пространстве, благодаря этому можно уменьшить габариты акустоэлектронных приборов. К основным преимуществам таких приборов можно также отнести простоту конструкции, хорошую воспроизводимость характеристик, высокую температурную стабильность и малое потребление энергии.

Конструктивно акустоэлектронные приборы на ПАВ (в простейшем виде) представляют собой подложку из кварца или ниобата лития, являющуюся звукопроводом, а преобразования сигналов осуществляются электроакустическими преобразователями.

Электроакустические преобразователи выполняют в виде двух металлических изолированных гребенок, чаще всего встречно-штыревой структуры (рис. 132).

Рабочая частота приборов на ПАВ определяется расстоянием между штырями гребенок преобразователя (это расстояние обычно равно половине длины ПАВ), полоса пропускания зависит от числа пар штырей и обратно пропорциональна числу встречно-штыревых пар (практически составляет 1 – 60% центральной рабочей частоты). Например, на частоте 100 МГц длина ПАВ в подложке из ниобата лития составляет 35 мкм, ширина штырей – 8,75, длина – 2700, расстояние между штырями – 17,5 мкм. Верхний предел диапазона рабочих частот приборов на ПАВ зависит от технологии изготовления преобразователей (ее разрешающей способности) и располагается в пределах нескольких гигагерц.

Акустоэлектронные приборы используют в качестве фильтров (см. § 54), линий задержки, генераторов, усилителей и запоминающих устройств.

Линии задержки на ПАВ характеризуются диапазоном рабочих частот от десятка до тысяч мегагерц, временем задержки от наносекунд до десятков микросекунд и относительно небольшими потерями. Генераторы на ПАВ отличаются высокой стабильностью и работают до частот в несколько мегагерц без использования умножителей.

Эффективны различные приборы на основе ПАВ, где осуществляется взаимодействие акустических волн и носителей заряда в полупроводниках. На таком взаимодействии основана работа различных устройств обработки информации. Благодаря использованию акустооптических явлений можно создать компактные и многофункциональные устройства управления лазерным лучом.

Тема 3.2 ЛИНИИ ЗАДЕРЖКИ НА ПОВЕРХНОСТНЫХ АКУСТИЧЕСКИХ ВОЛНАХ

Дата добавления: 2014-01-07