Связи и реакции связей

Связью называется ограничение, налагаемое на положения и

скорости точек механической системы.

Реакциями связей называются силы, действующие на систему со стороны материальных тел, осуществляющих связи, наложенные на эту систему.

При определении реакций связи используется принцип освобождения от связей: любое несвободное тело можно рассматривать как свободное, если условно освободить его от связей и заменить их действие на тело реакциями связей.

Например: балка, стоящая на опорах (Рис. 2 а)

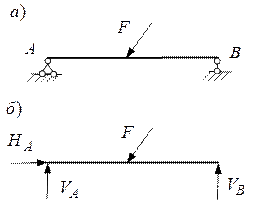
Рис. 2, а, б

и освобождение от опор (Рис. 2,б), действие которых имитируют реакции , , .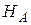

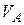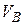2.2.Система сходящихся сил и момент силы относительно точки.

Система сил, линии действия которых пересекаются в одной точке, называются системой сходящихся сил.

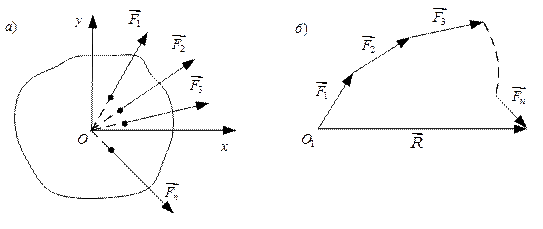
Рис. 3, а, б

Рассмотрим произвольную систему n сходящихся сил (,,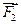,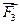…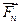), приложенных к плоскому твердому телу в разных точках (рис. 3, а). Найдем равнодействующую этих сил 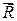графически и аналитически.

Сложение сил 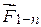выполним по правилу силового многоугольника.

последовательно друг за другом (рис. 3, б). Вектор 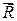будет равнодействующей системы сил .

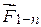В случае, если 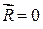, то система сил 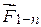будет уравновешенной, равнодействующая 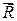равна нулю.

Для аналитического определения 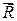введем прямоугольную систему координат 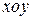и спроектируем все силы на ос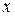и и 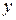. Получим

.

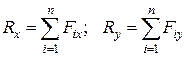Для уравновешенной системы 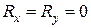и

.

Таким образом, два предыдущих уравнения говорят об уравновешенной системе сил, действующих на неподвижное тело, и называются двумя уравнениями статики.

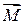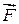Модулем момента силы относительно точки О называется величина, равная произведению величины силы 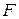на плечо 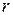, длина которого равна длине перпендикуляра, опущенного из рассматриваемой точки на линию действия силы (Рис. 4).

Рис. 4

Знак модуля момента: если сила 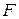“вращает” плечо 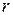против часовой стрелки - 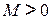, если наоборот - .

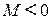Момент силы относительно точки является мерой вращательного действия этой силы на тело.

Теорема Вариньона. Если система сил, приложенных к твердому телу, имеет равнодействующую, то момент равнодействующей относительно любой точки тела равен сумме моментов всех сил относительно этой точки.

Если равнодействующая равна нулю, то

.

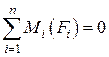2.3. Понятие о расчётной схеме конструкции или сооружения.

В прикладной механике прибегают к упрощению условий задач, отказываясь от учёта целого ряда сравнительно менее важных факторов и оперируют с расчётными схемами вместо точного описания сооружений, машин и механизмов.

2.3.1. Классификация расчётных схем конструкций.

С геометрической точки зрения конструкции бывают:

1. составленными из стержней, т.е. из таких элементов, у которых один размер (длина) значительно превышает два других – эти конструкции будем называть стержневыми. Частный случай такой конструкции – стержень.

2. составленными из элементов, у которых размеры по двум направлениям (длина и ширина) значительно превосходят размер по третьему направлению (толщину); такие элементы носят название пластинок, плит и оболочек.

3. такими, у которых все три размера одного и того-же порядка. Их называют массивами, сплошными средами или телами.

Стержневые системы разделяются на плоские и пространственные.

Плоские системы – системы, в которых оси всех стержней включая опорные и линии действия внешних сил лежат в одной плоскости; пространственные – такие, в которых это условие не соблюдено.

Пространства в “Прикладной механике” подчиняются геометрии Эвклида.

С кинематической точки зрения системы делятся на:

1. геометрически неизменяемые и неподвижные, имеющие лишь необходимое для этого число кинематических связей;

2. геометрически неизменяемые и неподвижные, имеющие сверх необходимых связей некоторое количество лишних;

3. геометрически изменяемые.

Геометрически неизменяемой называется такая система, в которой изменение формы обусловливается лишь деформацией материала.

С точки зрения характера взаимного соединения элементов различают конструкции:

1. с шарнирными соединениями;

2. с жёсткими соединениями;

3. комбинированные.

С точки зрения направления опорных реакций конструкции бывают:

1. безраспорные, с вертикальными опорными реакциями.

2. распорные.

Дата добавления: 2014-01-07