Синдромное декодирование сверточных кодов

Предположим, что нами принята полубесконечная последовательность r, состоящая из слова сверточного кода и вектора ошибки:

r = U + e. (4.9)

Аналогично тому, как это делается для блочных кодов, можно вычислить синдром принятой последовательности:

S = r× H = e × Н. (4.10)

Однако из-за бесконечной длины принятой последовательности (а сверточный код представляет собой непрерывную бесконечную последовательность двоичных символов) синдром также будет иметь бесконечную длину и его прямое вычисление не имеет смысла.

Вместе с тем можно заметить, что для рассмотренных нами сверточных кодов влияние одного информационного кадра распространяется всего на несколько кодовых кадров. Поэтому декодер может просматривать не весь синдром, а вычислять его компоненты по мере поступления кадров кодовой последовательности, исправлять текущие ошибки и сбрасывать те компоненты синдрома, которые вычислены давно.

Для исправления ошибок при этом декодер должен содержать таблицу сегментов синдромов и сегментов конфигураций ошибок, образующих данные конфигурации синдрома. Если декодер находит в таблице полученный сегмент синдрома, он исправляет начальный сегмент кодового слова.

Схема декодера для сверточного (12,9)-кода Вайнера-Эша изображена ниже (рис. 4.4). Исправление ошибок с помощью данного декодера производится на сегментах из трех кодовых кадров - n = 12.

Декодер работает следующим образом. Во входной регистр записывается первый кадр принимаемой последовательности r (четыре символа). По первым трем (информационным) символам кадра по тем же правилам, что и при кодировании, определяется значение контрольного бита, который далее сравнивается с четвертым (проверочным) символом принятого кадра.

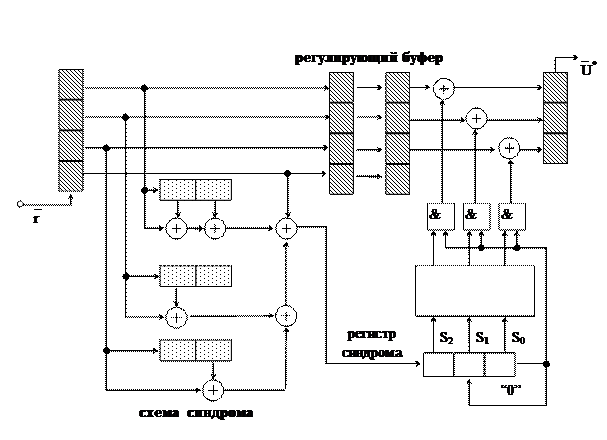
Рис. 4.4

При совпадении контрольного и проверочного битов (а это будет, если ошибки в первом кадре нет) в первую ячейку синдромного регистра записывается 0, если же в кадре ошибка есть, − то 1. Далее первый кадр принятой последовательности переносится в регулирующий буфер, а во входной регистр заносится очередной кадр принятой последовательности.

После аналогичных проверок для второго и третьего кадров принятой последовательности на выходе регулирующего буфера оказывается первый кадр принятой последовательности, в регистре синдрома — трехбитовый синдром, соответствующий принятому сегменту из трех кадров, а на выходе адресной логики — дешифрированный по синдрому S вектор ошибки e.

Исправленный кадр записывается в выходной регистр, при этом исправление производится только при наличии единицы на входах схем “ И ”, что соответствует присутствию ошибки именно в первом кадре. После исправления ошибки регистр синдрома сбрасывается. Потеря второго и третьего битов синдрома при этом не имеет значения, так как ни во втором, ни в третьем кадрах ошибки быть не должно (она была в первом кадре, а значит, во фрагменте из трех кадров ошибки больше быть не должно).

Все возможные конфигурации ошибок в первых трех кадрах и соответствующие им первые три бита синдрома приведены в табл. 4.2.

Таблица 4.2

Конфигурация ошибок в принятом сегменте	Синдром
1-й кадр	2-й кадр	3-й кадр	…	…

Дата добавления: 2014-01-07