Группа подобий евклидова пространства

Ordm;.

Определитель Грама. Объем в евклидовом пространстве.

Определение 1: пусть 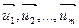- произвольная система векторов 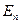. Определителем Грама этой системы векторов называется определитель m -го порядка вида:

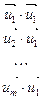
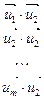
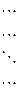
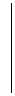(1)

Грам Йёрген (1850-1916) - датский математик. Определитель Грама обладает свойствами (доказаны в алгебре):

1) он всегда неотрицателен;

2) система векторов 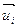, , 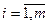линейно независима тогда и только тогда, когда её определитель Грама положителен.

Замечание 1: из аналитической геометрии известно, что объем параллелепипеда, построенного на трёх неколлинеарных векторах равен произведению площади параллелограмма, построенного на векторах 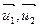, и длины перпендикуляра, опущенного из конца вектора 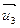на плоскость векторов .

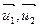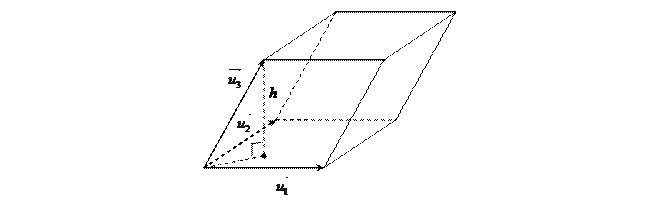
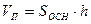
Обобщим понятие объёма трехмерного параллелепипеда на случаи больших размерностей.

Как известно, в пространстве 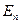, параллелепипедом, построенным на m - линейно независимых векторах 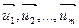, называется множество векторов вида 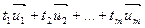, где параметры 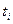, , 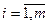независимо друг от друга изменяются на отрезке 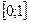. Назовём основанием этого параллелепипеда (m-1) - мерный параллелепипед натянутый на векторы , а расстояние от конца вектора до плоскости 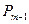, натянутой на векторы , назовём высотой исходного параллелепипеда. «Объёмом» одномерного параллелепипеда 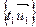назовем длину вектора 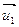. Для больших размерностей объём определим индуктивно, как объём основания, умноженной на высоту.

Теорема 1: квадрат объёма m-мерного параллелепипеда равен определителю Грама совокупности векторов :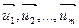

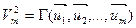(2)

□ Применим метод математической индукции по числу m векторов.

1) Для m=1 имеем: 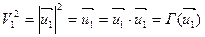- утверждение теоремы справедливо.

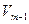2) Докажем что теорема имеет место для (m-1) векторов и докажем ёё справедливость для m векторов. Обозначим через ортогональную проекцию вектора на ортогональное дополнение к подпространству , натянутому на векторы . Эта проекция осуществляется параллельно подпространству 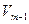, поэтому

, ,

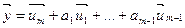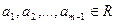причём 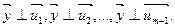(3)

Прибавим к последнему столбцу определителя Грама (1) предшествующие столбцы, соответственно умноженные на коэффициенты . Так как скалярное произведение линейно по второму аргументу, то получим в последнем столбце числа 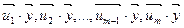, причём первые (m-1) из них равны нулю (- ортогональная проекция на ). Последний элемент последнего столбца равен

.

Длина вектора равна высоте параллелепипеда, поэтому

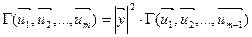(4)

Согласно индуктивному предположению определитель Грама из правой части равенства (4) есть квадрат объёма основания. Следовательно:

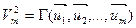
и теорема доказана. ■

2º.Объём n-мерного параллелепипеда в n-мерном евклидовом пространстве.

Пусть в пространстве 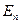задана линейно независимая система из n -векторов , а матрица А=(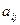), , имеет своими столбцами координаты этих векторов 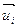в некотором ортонормированном базисе 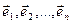. Тогда для матрицы 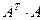рассмотрим элемент . . 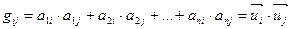То есть матрица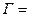 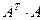является матрицей Грама системы векторов .

Так как 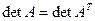, то (5)

Из равенства (2) следует что .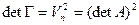

Теорема 2: квадрат объёма n-мерного параллелепипеда равен квадрату определителя матрицы 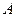или . (6)

§14. Группа движений евклидова пространства.

Определение 1: движением пространства 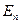называется его аффинное преобразование, не меняющее расстояние между точками.

Замечание 1: из определения расстояния между точками (§11) следует, что ассоциированное с движением векторное преобразование сохраняет длины векторов, значит, является ортогональным преобразованием, кроме того при этом преобразовании не меняются скалярное произведение и углы между векторами.

Определение 2: система координат называется прямоугольной декартовой или ортонормированной, если векторы 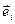образуют ортонормированный базис векторного евклидова пространства 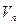, связанной с .

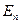Замечание 2: при движении ортонормированная система координат отображается также на ортонормированную систему координат.

Следующие теоремы являются непосредственными следствиями аналогичных теорем из §8 и теоремы (3) из §10.

Теорема 1: при движении пространства 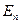координаты 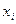произвольной точки М и координаты 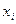её образа Мв одной и той же ПДСК связаны формулами вида:

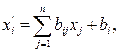(1)

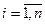
где матрица (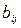) ортогональна.

Если 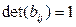, то движение (1) I рода, если же 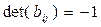, то это движение II рода.

Теорема 2: всякое преобразование пространства 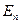вида (1) с ортогональной матрицей (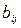), является движением.

Теорема 3: движение пространства 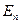вполне определяется заданием двух соответствующих ортонормированных систем координат (реперов).

Теорема 4: множество движений пространства Е_n является группой.

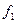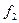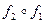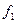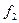□ 1) Так как движения и - аффинные преобразования, то и их композиция - аффинное преобразование согласно теореме (1) из §9. Так как и не меняют расстояний между точками, то 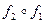также не меняют расстояний между точками, а значит, является движением.

2) Так как движение 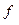- аффинное преобразование, то - также аффинное преобразование. Так как 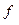сохраняет расстояние между точками, то также сохраняет расстояние между точками, а значит, является движением. ■

Рассмотрим подгруппы группы движений.

1º. Параллельный перенос задается формулами вида:

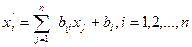где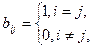

то есть формулами .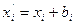

Следовательно, матрица (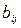) является единичной. Но единичная матрица ортогональна и по теореме (2) параллельный перенос является движением. Группа параллельных переносов является подгруппой группы движений пространства Е_n.

2º. Движение, оставляющее неподвижной некоторую точку S, называется вращением вокруг центра S. Вращение является частным случаем центроаффинного преобразования (§9). Его формулы имеют такой же вид, что и формулы центроаффинного преобразования, но матрица (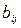) ортогональна. Очевидно, вращение с данным центром S образуют подгруппу группы всех движений пространства Е_n.

Как и в §9 указывается, что любое движение может быть представлено в виде композиции вращения и параллельного переноса.

Определение 3: Евклидовой геометрией называется наука, изучающая те свойства пространства Е_n, которые не изменяются при любых движениях этого пространства.

Замечание 3: элементарная геометрия – это евклидова геометрия пространств Е₂ и Е₃. Так как движение является частным случаем аффинного преобразования, то любое свойство фигуры, сохраняющееся при любом аффинном преобразовании, будет сохраняться и при движении. Поэтому все свойства фигур, изучаемые в аффинной геометрии, изучаются также и в евклидовой геометрии. Однако евклидова геометрия значительно богаче по содержанию, чем аффинная геометрия, так как в ней рассматриваются метрические понятия, отсутствующие в аффинной геометрии.

Определение 1: подобием пространства Е_п называется его аффинное преобразование, при котором все расстояния между точками умножаются на одно и то же положительное число k, называемое коэффициентом подобия.

Определение 2: фигура F₁ называется подобной фигуре F₂, если существует подобие, отображающее F₁ на F₂.

Пример: любое движение является подобием с коэффициентом k=1.

Теорема 1: гомотетия с коэффициентом k ≠ 0 является подобием с коэффициентом |k|.

□ Гомотетия с центром S(S_i) и коэффициентом k задается в аффинной, в частности, прямоугольной декартовой системе координат формулами вида:

(1) 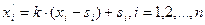(см. §9)

Пусть точки M(x_i) и N(y_i) отображаются при гомотетии соответственно на точки M'(x_i) и N'(y_i). Так как 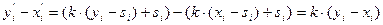, то по формуле расстояния между точками получаем: ■

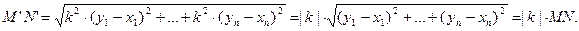Теорема 2: множество подобий пространства Е_п является группой.

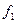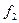□ 1) Пусть и - подобия с коэффициентами k₁ и k₂. Так как это аффинное преобразование, то и их композиция 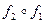- аффинное преобразование. При подобии 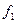все расстояния умножаются на коэффициент k₁, а при подобии 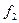все расстояния умножаются на k₂, тогда при 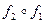все расстояния умножаются на .

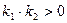Значит, 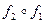- подобие с коэффициентом k₁∙k₂.

2) Пусть 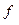- подобие с коэффициентом k. Так как это аффинное преобразование, то и - аффинное преобразование. При 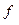все расстояния умножаются на число k, при они умножаются на число , поэтому является подобием. ■

Теорема 3: всякое подобие с коэффициентом k можно представить в виде композиции гомотетии (с тем же коэффициентом и любым центром) и некоторого движения.

□ Пусть 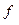- подобие с коэффициентом k, а g – гомотетия с этим же коэффициентом. Тогда 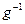- гомотетия с коэффициентом . Преобразование (2), является композицией подобия с коэффициентами k и , есть подобие с коэффициентом k ∙=1, то есть движение. Но тогда получаем из формулы (2): 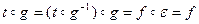и требуемое доказано. ■

Следующие три теоремы выражают свойства подобий.

Теорема 4: при подобии с коэффициентом k длины всех векторов умножаются на число k, а все скалярные произведения векторов на k².

□ Воспользуемся теоремой (3): 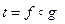. Так как векторное преобразование, ассоциирование с движением t, является ортогональным, то оно не меняет длин и скалярных произведений векторов (см. §10).

Векторное произведение, ассоциированное с гомотетией g, имеет вид: 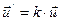, тогда при нем все длины векторов умножаются на k, а все скалярные произведения на k².

, . ■

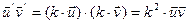Теорема 5: подобие не изменяет углы между векторами.

□ Пусть 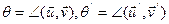, тогда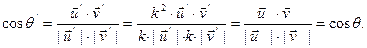

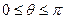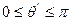Так как по определению угла между векторами и , то . ■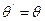

Теорема 6: подобие с коэффициентом k задается в прямоугольной декартовой системе координат формулами вида: 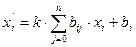, (3) где 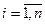, а матрица (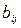) ортогональна.

□ Согласно теореме (3) данное подобие представимо в виде композиции гомотетии центром в начале координат и коэффициентом k:

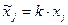(4)

и некоторого движения: 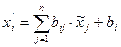(5)

Подставляя значения (4) в (5), получаем (3). ■

Дата добавления: 2014-01-07