Понятие квадрики

Виду.

Приведение квадратичной формы к каноническому

Доказательство основной теоремы опирается на две леммы.

Лемма 1: если квадратичная форма

(1)

не содержит квадратов переменных, то с помощью линейного преобразования её можно перевести в форму, содержащую квадрат хотя бы одной переменной.

□ По условию форма 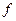содержит лишь члены с произведениями переменных, пусть 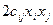при i≠j и 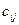≠0 – один из таких членов. Применим линейное преобразование переменных:

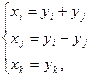, k≠i, k≠j.

Её определитель отличен от нуля.

Квадратичная форма 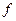будет содержать даже два члена с квадратными переменными:

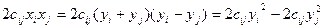
Эти слагаемые не могут исчезнуть при приведении подобных членов, так как любое из остальных слагаемых содержит хотя бы одну переменную, отличную 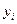или . ■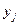

Лемма 2: если квадратичная форма (1) содержит член 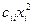и ещё хотя бы один член с этой переменной 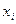, то с помощью линейного преобразования её можно перевести в форму от переменных 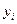вида:

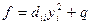(2)

где q – квадратичная форма от n – 1 переменной, не содержащей переменной .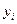

□ 1.) Выделим в квадратичной форме (1) сумму членов с переменной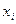

,

где 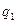- сумма остальных членов, не содержащих .

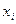2.) Обозначим

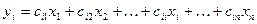
по правилу нахождения квадрата многочлена найдем и в полученном выражении выделим также сумму членов с переменной 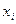. Таковым будет квадрат члена 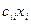и удвоенные произведения этого члена на остальные члены многочлена:

(4)

где 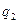- сумма членов, не содержащих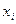

3.) Разделим обе части равенства (4) на 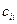≠0 и вычтем полученное равенство почленно из равенства (3). Приведя подобные члены, получим следующее:

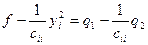
Выражение в правой части не содержит переменной 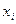и является квадратичной формой от n-1 переменных 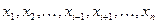. Обозначим её через q, а коэффициент 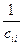- через 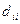. Тогда получим равенство:

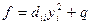
4.) Произведем линейные преобразования переменных:

Её определитель отличен от нуля. Тогда q есть квадратичная форма от n-1 переменных , а квадратичная форма 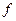приведена к виду (2). ■

Теорема (основная): всякая квадратичная форма может быть приведена к каноническому виду с помощью линейного преобразования переменных.

□ 1.) Если квадратичная форма (1) не содержит квадратов переменных, то, используя лемму (1), приведем её с помощью линейного преобразования к виду, содержащему квадрат хотя бы одной переменной.

2.) Далее в соответствие с леммой 2 при помощи ещё одного линейного преобразования переменных переведём полученную квадратичную форму в сумму члена с квадратом какой- либо переменной и квадратичной формы от остальных n-1 переменных. Применяем описанный процесс до тех пор, пока исходная квадратичная форма станет содержать лишь квадраты переменных, то есть канонический вид:

(5)

где m ≤ n и 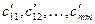отличны от нуля. ■

Следствие: любая квадратичная форма может быть приведена к нормальному виду с помощью линейного преобразования переменных.

□ Применим к квадратичной форме канонического вида (5) линейное преобразование переменных:

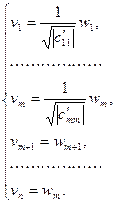(6)

с неравным нулю определителем.

Квадратичная форма примет нормальный вид:

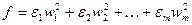(7)

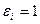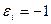где при и при . ■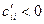

Замечания: 1.) линейное преобразование переменных, непосредственно приводящее квадратичную форму (1) к виду (7), является композицией всех линейных преобразований переменных, используемых в основной теореме и её следствии;

2.) выполняя различные линейные преобразования переменных, в итоге можно получить отличающиеся по внешнему виду окончательные результаты;

3.) описанный в теореме способ приведения квадратичной формы к каноническому виду применяется на практике; он был предложен известным французским математиком Ж. Л. Лагранжем (1736 - 1813);

4.) квадратичные формы имеют важное свойство, называемое законом инерции. Это свойство выражает следующая теорема.

Теорема 2: если квадратичная форма приведена к каноническому виду с помощью двух различных линейных преобразований переменных, то число р положительных коэффициентов при квадратах новых переменных, так же как и число q отрицательных коэффициентов, будет в обоих случаях одно и то же.

Из закона инерции следует, что число p + q всех ненулевых коэффициентов в каноническом виде квадратичной формы не зависит от способа её приведения к каноническому виду. Это число p + q называется рангом квадратичной формы и всегда равно рангу её матрицы, а число р называется положительным индексом квадратичной формы. Квадратичная форма называется положительно определенной, если при любых одновременно не равных нулю значениях переменных она принимает положительные значения.

Определение 1: квадрикой в аффинном пространстве 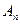называется множество точек, координаты которых в некоторой аффинной системе координат 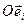удовлетворяют уравнению второй степени:

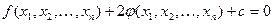(1)

где 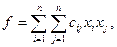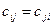- квадратичная форма,

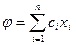- линейная форма, – свободный член.

Теорема 1: понятие квадрики не зависит от выбора аффинной системы координат.

□ Если множество точек задано в старой системе координат 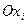уравнением (1), то для получения уравнения этого множества точек в новой системе координат достаточно применить формулы преобразования координат точки (§2):

, , .

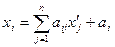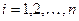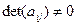При этом не могут появиться члены степени выше второй, то есть степень уравнения (1) не может повыситься. Степень этого уравнения не может понизиться. Если бы степень нового уравнения оказалась ниже второй, то при обратном переходе от этого уравнения к уравнению (1) она бы повысилась до второй. Выше доказано, что это невозможно. ■

Примеры: 1.) на аффинной плоскости 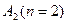квадрика является линией второго порядка и задается уравнением:

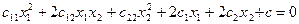
2.) в пространстве 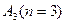квадрика является поверхностью второго порядка и имеет уравнение:

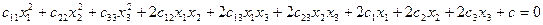
Определение 2: точк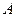и и 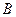называются симметричными относительно точки 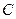пространства 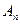, если 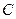есть середина отрезка 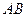, то есть .

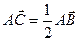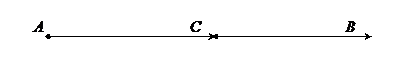
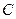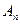Определение 3: точка называется центром симметрии или просто центром квадрика пространства , если точка 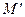, симметричная любой точке квадрики относительно точки 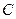, также принадлежит этой квадрике.

,

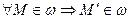
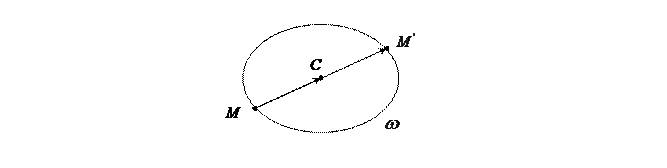
Определение 4: Квадрика называется центральной, если она имеет единственный центр, и нецентральной, если не имеет цента.

Если множество центров квадрики является бесконечным и все эти центры принадлежат r -мерной плоскости P_r (1≤r<n) пространства A_n,то говорят, что данная квадрика имеет плоскость центров размерности r.

Дата добавления: 2014-01-07