
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные правила комбинаторики. Выборки, сочетания. Аксиомы теории вероятностей
|
|
|
|
Аксиомы теории вероятностей. Дискретные пространства элементарных исходов. Классическое определение вероятности
Пусть Ω пространство элементарных исходов, F – множество всех подмножеств Ω. Любому событию A 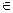 F ставится в соответствие действительное число P(A), называемое вероятностью события A, при этом выполняются аксиомы теории вероятности:
F ставится в соответствие действительное число P(A), называемое вероятностью события A, при этом выполняются аксиомы теории вероятности:
Аксиома 4.1. Вероятность произвольного события неотрицательна, т.е. 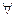 A
A 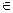 F, P(A)
F, P(A) 0.
0.
Аксиома 4.2. Вероятность достоверного события равна 1, т.е. P(Ω)=1.
Аксиома 4.3. (счетной аддитивности) Если A1, A2,… 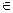 F и Ai∙ Aj= Ø (i
F и Ai∙ Aj= Ø (i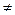 j), то P(A1+ A2+…) = P(A1) + P(A2) +… или P(
j), то P(A1+ A2+…) = P(A1) + P(A2) +… или P(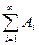 ) =
) =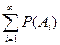 .
.
Определение 4.4. Бесконечное множество называется счетным, если элементы этого множества можно занумеровать натуральными числами.
Все другие множества называются несчетными (например, множество точек [a,b] ненулевой длины).
Определение 4.5. Пространство элементарных исходов называется дискретным, если оно конечное или счетное, т.е. Ω={ω1, …, ωn} или Ω={ω1, ω2,… }.
Любому элементарному исходу ωi ставится в соответствие число p(ωi), так что при этом 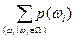 =1.
=1.
Определение 4.6. Вероятностью события A называется число P(A)=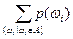 .
.
Пример 4.7. Бросается игральная кость. Найти вероятность выпадения нечетного числа очков.
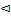 p(ωi)=
p(ωi)=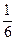 , i =1,..,6,
, i =1,..,6,  P(A)= p(ω1, ω3, ω5)=
P(A)= p(ω1, ω3, ω5)= 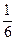 +
+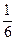 +
+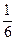 =
= 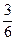 =
= 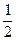 .
. 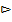
Сформулируем следующие предположения:
1. Пространство элементарных исходов конечно: Ω={ω1, …, ωn}.
2. Все элементарные исходы равновероятны (равновозможны), т.е. p(ω1)= p(ω2)=…= p(ωn).
Поскольку 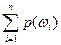 =1, то p(ωi)=
=1, то p(ωi)=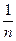 , i =1,.., n.
, i =1,.., n.
Рассмотрим некоторое событие A 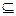 Ω, состоящее из k элементарных исходов, k
Ω, состоящее из k элементарных исходов, k 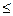 n, A= {
n, A= {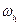 ,
, 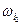 ,…,
,…,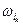 }.
}.
Вероятность события P(A)=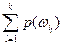 =
= 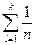 =
=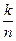 .
.
Определение 4.8. (классическое определение вероятности) Если пространство элементарных исходов конечно, а все элементарные исходы равновероятны, то вероятность события A называется отношение числа элементарных исходов, благоприятствующих A, к общему числу всех возможных элементарных исходов P(A)=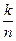 .
.
Пример 4.9. Бросается две монеты. Найти вероятность того, что хотя бы на одной выпадет герб.
 Ω={(г,г), (г,р), (р,г), (р,р)}, n= 4.
Ω={(г,г), (г,р), (р,г), (р,р)}, n= 4.
A= {(г,г), (г,р), (р,г)}, k =3.
Таким образом, P(A)=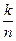 =
= 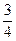 .
. 
Пример 4.10. Бросаются две игральные кости. Какова вероятность того, что сумма выпавших очков равна 7?
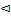 Ω={(i,j) | i,j
Ω={(i,j) | i,j 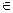 {1,..,6}}, n= 36,
{1,..,6}}, n= 36,
A= { (6,1), (5,2), (4,3), (3,5), (2,5), (1,6)}, k =6,
Таким образом, P(A)=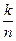 =
= 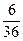 =
=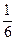 .
. 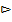
Лемма 5.1. Из m элементов a1,…, an первой группы и n элементов b1,…,bn второй группы можно составить ровно m∙n упорядоченных пар вида (ai, bj), содержащих по одному элементу из каждой группы.
 (a1, b1), (a1, b2), …, (a1, bn), Всего m∙n пар
(a1, b1), (a1, b2), …, (a1, bn), Всего m∙n пар 
(a2, b1), (a2, b2), …, (a2, bn), m строк
… … … … … …...
(am, b1), (am, b2), …, (am, bn).
n столбцов
Пример 5.2. В колоде карт 4 масти (черва, пика, трефа, бубна), в каждой масти по 9 карт или по 13 карт, тогда в колоде либо n=4∙9=36 карт, либо n=4∙13=52 карты.
Лемма 5.3. Из n1 элементов первой группы a1, a2,…, 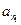 ,
,
n2 элементов второй группы b1, b2,…, 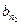 ,
,
и т.д. … … … … … … … …
nk элементов k -той группы x1, x2,…, 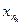 .
.
можно составить ровно n1 ∙ n2 ∙…∙ nk различных упорядоченных комбинаций вида (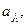
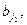 …,
…,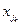 ), содержащих по одному элементу из каждой группы.
), содержащих по одному элементу из каждой группы.
Пример 5.4. При бросании двух игральных костей число различных упорядоченных комбинаций следующее: N = 62 = 36;при бросании трех костей – N=63=216.
Леммы 5.1 и 5.3 называются основными правилами комбинаторики.
Пусть имеется множество из n элементов { a1, a2,…, an }. Будем рассматривать выборки объёма k вида (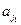 ,
,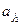 , …,
, …, 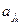 ) из n элементов. Все выборки можно классифицировать по двум признакам:
) из n элементов. Все выборки можно классифицировать по двум признакам:
1) упорядоченные и неупорядоченные;
2) с возвращением и без возвращения.
Если выборки считаются упорядоченными, то играет роль порядок элементов в выборке. Если же выборка неупорядоченная, то все выборки с одним и тем же составом элементов отождествляются.
Пример 5.5. Рассмотрим множество, состоящее из трёх элементов {1,2,3}. Составим таблицу числа выборок объёма k =2 из трёх элементов.
| (1,1), (1,2), (1,3) (2,1), (2,2), (2,3) (3,1), (3,2), (3,3) | (1,1), (1,2), (1,3) (2,2), (2,3) (3,3) | с возвращением |
| (1,2), (1,3) (2,1), (2,3) (3,1), (3,2) | (1,2), (1,3) (2,3) | без возвращения |
| упорядоченные | неупорядоченные | выборки |
Общая таблица числа выборок объёма 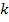 из
из 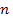 элементов:
элементов:
| nk | 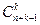
| с возвращением |
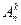
| 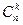
| без возвращения |
| упорядоченные | неупорядоченные | выборки |
Определение 5.6. Упорядоченная выборка без возвращения называется размещением.
Число размещений 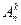 =
=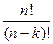 .
.
Пример 5.7. В лифт 12-этажного дома зашли 3 человека. Найти вероятность того, что все вышли на разных этажах.
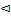 Ω={(i1, i2, i3) | i1, i2, i3
Ω={(i1, i2, i3) | i1, i2, i3 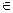 {2,3,…,12}},{ i1
{2,3,…,12}},{ i1 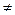 i2, i2
i2, i2 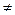 i3 } –
i3 } – дополнительное условие для события А. Первое (Ω –
дополнительное условие для события А. Первое (Ω – упорядоченные выборки с возвращением, n =113. Число благоприятствующих исходов k =
упорядоченные выборки с возвращением, n =113. Число благоприятствующих исходов k =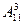 =
=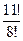 =9∙10∙11. По классическому определению вероятности Р(А)=
=9∙10∙11. По классическому определению вероятности Р(А)=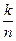 =
=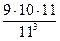 =
=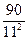 =
=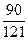 .
. 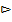
Определение 5.8. Перестановкой из k элементов называется совокупность этих же элементов, записанных в произвольном порядке. Число перестановок из k элементов Pk = k! (0!=1).
Определение 5.9. Произвольное k -элементное подмножество множества, состоящего из n элементов, называется сочетанием из n элементов по k элементов.
Обозначается число сочетаний из n элементов по k элементов через
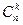 =
=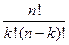 ; k
; k 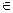 {0,1,…, n }.
{0,1,…, n }.
Свойства сочетаний:
1) 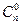 =
=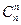 =1;
=1;
2) 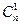 =
=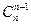 = n;
= n;
3) 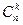 =
=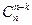 ;
;
4) 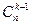 +
+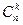 =
= .
.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1084; Нарушение авторских прав?; Мы поможем в написании вашей работы!