Случайные величины. Определение 12.1. Случайной величиной Х называется функция Х(ω), отображающая пространство элементарных исходов Ω во множество действительных чисел

Определение 12.1. Случайной величиной Х называется функция Х(ω), отображающая пространство элементарных исходов Ω во множество действительных чисел 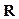. Т.о. Х(ω): Ω→.

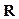Пример 12.2. Дважды подбрасывается монета. Рассмотрим случайную величину Х – число выпадений герба, определённую на пространстве элементарных исходов Ω={(г,г),(г,p),(p,г),(p,p)}. Множество возможных значений случайной величины Х-{0,1,2}. Составим таблицу

ω	(г,г)	(г,p)	(p,г)	(p,p)
Х(ω)

Одной из важнейших характеристик случайной величины является её функция распределения.

Определение 12.3. Функцией распределения случайной величины Х называется функция F(x)=F _X (x) действительной переменной х, определяющая вероятность того, что случайная величина X примет в результате эксперимента значение, меньшее некоторого фиксированного числа х

F(x)=P{ X< x }=P{ X 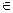(-∞; x)}.

Замечание 12.4. Если рассматривать случайную величину Х как случайную точку на оси O x, то функция распределения F(x) с 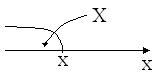геометрической точки зрения – это вероятность того, что случайная точка Х в результате реализации эксперимента попадёт левее точки х.

Свойства функции распределения

Свойство 12.5. Функция распределения F(x) – неубывающая функция, т.е.для 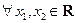таких, что 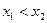выполняется условие 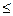F(x) F(x).

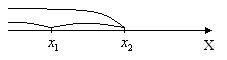
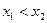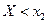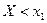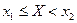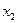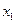Поскольку , то события {}={}+{}, по определению функции распределения F()=F()+P{}.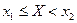

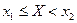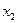Т.к. P{}0, то F()>F().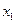

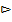
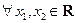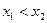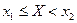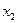Свойство 12.6. Для таких, чтосправедливо равенство P{}= F()–F().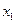

Замечание 12.7. Если функция распределения F(x) – непрерывная, то свойство 12.6 выполняется и при замене знаков 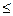и < на < и .

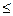Свойство 12.8. 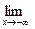F(x)=0; 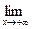F(x)=1.

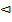F(-∞)=P{ X < -∞ }=P(Ø)=0, F(+ ∞)=P{ X <+ ∞ }=P(Ω)=1.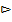

Свойство 12.9. Функция распределения F(x) непрерывна слева (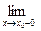F(x)=F()).

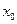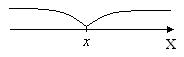Свойство 12.10. P{ Xx }=1-F(x).

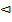{ X<+∞ }={ X<x }+{ Xx }, по свойству вероятности P{ X<+∞ }=P{ X<x }+P{ Xx };

P(Ω)=1= F(x)+ P{ Xx }, откуда P{ Xx }=1- F(x).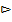

Дата добавления: 2014-01-07